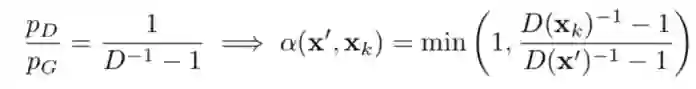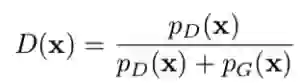Uber提出基于Metropolis-Hastings算法的GAN改进思想

2019 年 1 月 11 日 AI前线

作者｜Ryan Turner 等

编译｜Alex

编辑｜Debra

AI 前线导读：改进 GAN 除了使用更复杂的网络结构和损失函数外，还有其他简单易行的方法吗？Uber 的这篇文章或许可以给你答案，将 GAN 与贝叶斯方法相结合，在已经训练好的 GAN 上增加后处理步骤即可。本文对 Uber 的这篇最新工作进行了简要介绍，如果对内容感兴趣还可以点击文末的原文链接阅读论文，同时文末还提供了该方法的开源代码，你可以轻松用它来提升自己的 GAN 模型。

更多干货内容请关注微信公众号“AI 前线”（ID：ai-front）

生成对抗网络（GAN）不仅在真实感图像生成和图像恢复方面取得了令人惊叹的效果，并且由 GAN 生成的一幅艺术作品也售出了 40 万美元的价格。

在 Uber，GAN 有大量具有潜力的应用，包括增强机器学习模型与对抗性攻击的对抗能力，学习交通模拟器，乘车请求或随时间变化的需求模式，以及为Uber Eats 生成个性化的订单建议（https://eng.uber.com/uber-eats-recommending-marketplace/）。

GAN 由两个互相对抗的部分组成，一部分是生成器，一部分是判别器。生成器学习真实数据的分布，判别器负责需要学习如何区别真实样本和生成样本（即假样本）。大多数研究都致力于改进 GAN 的结构和训练过程来提高其性能，例如使用更大的网络结构（https://arxiv.org/abs/1809.11096）或使用不同的损失函数。

NeurIPS2018 的贝叶斯深度学习研讨会（http://bayesiandeeplearning.org/）上，Uber 的一篇论文中提供了一种新的思路：调整判别器用于在完成训练后从生成器中选择更好的样本。该工作提供了一种互补的抽样方法，Google 和 U.C. Berkeley 在判别器舍选抽样（Discriminator Rejection Sampling，DRS https://arxiv.org/abs/1810.06758）的研究与此方法也具有相同的思路。

Uber 这篇工作以及 DRS 方法的核心思想可归纳为，如何使用已经训练好的判别器的信息来从生成器中选择样本，以保证这些被选择的样本尽可能符合真实数据的分布。通常，在训练完成后判别器就没有什么用了，因为在训练过程中会将判别器学到的知识编码到生成器中。然而，生成器往往是不完美的，判别器同时也会含有一些有用的信息，所以上述使用判别器信息来提升已经训练好的 GAN 的方法是值得一试的。Uber 的研究团队使用了 Metropolis-Hastings 算法对分布进行抽样，并将采用这种方法得到的模型称为 Metropolis-Hastings GAN，即 MH-GAN（https://en.wikipedia.org/wiki/Metropolis%E2%80%93Hastings_algorithm）。

GAN 重抽样

GAN 的训练过程通常被理解为两种条件之间的博弈，生成器需要尽可能让判别器产生误判的概率最大化，而判别器则需要尽可能的对真 1z 实数据和生成数据进行良好的区分。图 1 展示了这个过程，生成器使得函数值向极小值方向移动（橙色线条），而判别器则向极大值方向移动（紫色线条）。训练结束后，向生成器输入不同的随机噪声可以得到很方便得到生成样本。如果可以训练一个完美的生成器，那么生成器最终的概率密度函数 pG 应与真实数据的概率密度函数相同。然而，许多现有的 GAN无法很好地收敛到真实数据的分布（https://arxiv.org/abs/1706.08224），因此从这种不完美的生成器中抽样会产生看起来不像原始训练数据的样本。

这种 pG 的不完美让我们想到另一种分布情况：判别器对生成器隐含的概率密度。这种分布被称为 pD，并且它往往都很接近真实的数据分布 pG。这是因为训练判别器是一种比训练生成器更简单的任务，因此判别器很有可能包含可以用于校正生成器的信息。如果我们有一个完美的判别器 D 和一个不完美的生成器 G，使用 pD 而不是 pG 作为生成的概率密度函数等价于使用一个新的生成器 G'，并且这个 G'是可以完美地模拟真实数据分布的，如图一所示：

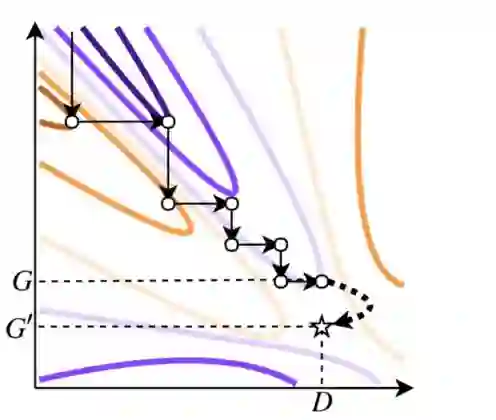
图 1：等高线图展示了 GAN 训练中的对抗过程，联合函数的值在极小化和极大化之间交替进行。橙色线条表示生成器 G 的优化过程，紫色线条表示判别器 D 的优化。假设 GAN 的训练过程结束于图中（D,G）这一点，此时的 G 未处于最优点，但对于这个 G 来说 D 是最优的。此时，通过从 pD 的分布中抽样，可以得到一个能够完美对数据分布建模的新的生成器 G'。

即使 pD 的分布可能与数据更匹配，但若想利用其得到样本数据并不像直接使用生成器那样直接。幸运的是，我们可以使用抽样算法从分布中产生样本，一种是舍选抽样法（Rejection Sampling，也被称为 Acceptance-Rejection Sampling），一种是马尔科夫链蒙特卡洛法（Markov Chain Monte Carlo，MCMC）。这两种方法都可以作为一种后处理方法来提高生成器的输出；之前的判别器舍选抽样法（Discrimitor Rejection Sampling，DRS）借鉴了舍选抽样法的思路，而 MH-GAN 则采用了 Metropolis-Hastings MCMC 方法。

舍选抽样

很多实际问题中，真实分布 p(x) 是很难直接抽样的的，因此，我们需要求助其他的手段来抽样。既然 p(x) 太复杂在程序中没法直接抽样，那么我们可以设定一个程序可抽样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，达到接近 p(x) 分布的目的，其中 q(x) 叫做候选分布（Proposal Distribution）。

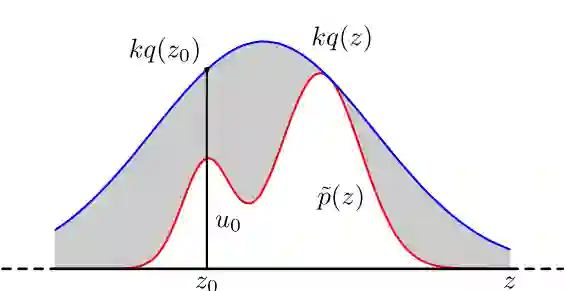
图 2: 舍选抽样

具体操作如下，设定一个方便抽样的函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。（参考上图）

x 轴方向：从 q(x) 分布抽样得到 a。
y 轴方向：从均匀分布（0, kq(a)) 中抽样得到 u。
如果刚好落到灰色区域即 u > p(a)，则拒绝，否则接受这次抽样。

重复以上过程便可得到 p(x) 的近似分布。该方法两大挑战分别是：

k 的值通常是人为经验设置的，无法确定一个准确的值。若 k 值设置的过大可能导致拒绝率很高，增加无用计算；若 k 值过小则有可能找不到正确的 p(x) 分布。
合适的 q(x) 分布通常很难找到。

在 GAN 中，pD 即为目标分布对应上述 p(x），pG 为现有的分布对应上述 q(x)。所以在 GAN 中使用该方法的难点主要来源于 k 值的确定，或因 k 值太小而无法正确抽样，或因 k 值过大而在高维空间中产生大量的计算。为了解决样本浪费问题，DRS 启发式地增加了一个γ调整判别器分数，使得判别器 D 即使是完美的情况下，从分布中产生的样本仍能够与真实样本存在差异。

更好的途径：Metropolis-Hastings

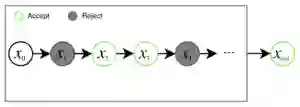
Uber 的这篇工作使用了 Metropolis-Hastings（MH）方法，这是马尔科夫链蒙特卡洛法一类方法中的一种。这一类方法被最初是作为舍选抽样法在高维空间中的代替而发明的，它们通过从候选分布中多点抽样得到一个尽可能复杂的概率分布，然后再对这个概率分布进行抽样。MH 包含两步，第一步是从候选分布中（例如，生成器）选择 K 个样本，然后从 K 中依次选择一个样本，决定是接受当前样本还是根据接受规则保留先前选择的样本，如图 3 所示：

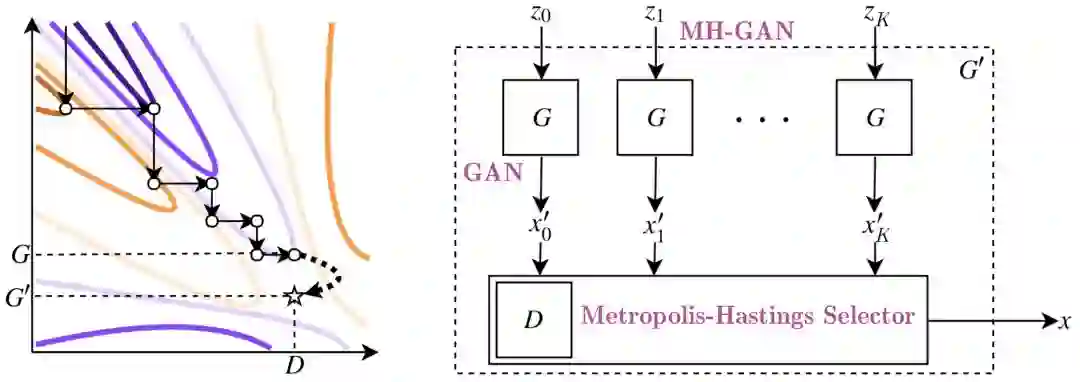
图 3：MH 在马尔科夫链中选择 K 个样本，然后根据接受规则对每个样本作出选择。这个马尔科夫链最终会输出最终接受的样本。对于 MH-GAN 而言，K 个样本由 G 生成，马尔科夫链的输出由改进后的 MH-GAN'的 G'产生

MH-GAN 最大的特点是接受概率可以仅由概率密度比值 pD/pG 计算得到，而 GAN'的判别器的输出恰巧可以计算这个比值！假设 xk 为初始样本，新的样本 x'可以通过与当前样本 xk 的概率 d 计算而被接受。

其中，D 是判别器分数，由以下公式得到

K 是一个超参数，对其调整可以在速度和置信度之间做出权衡。对于一个完美的判别器 K 趋近于无穷，即 D 的分布完美的接近了真实数据分布。

MH-GAN 更多细节

1. 独立抽样

噪声样本被独立地输入生成器，经过 K 次生成得到可以符合 MH 选择器条件的状态链。独立的链被用于从 MH-GAN 的生成器 G'中获取多样本。

2. 初始化

对于 MH 算法，由于初始点的不确定性，大部分情况下算法会经过一段长时的预烧期（http://people.csail.mit.edu/dsontag/courses/pgm13/slides/lecture9.pdf）才能开始有效的优化过程，即在开始接受第一个数据点之前会拒绝很大一部分数量的数据点。为了避免这种情况，本文对如何初始化状态链的方法进行了详细的介绍。在清理和初始化每一条状态链时，可以使用真实数据的采样结果对状态链进行优化。在遍历了整个状态链之后，如果没有一个数据被接受，MH-GAN 会从生成样本中重新开始抽样，从而确保真实数据中的样本不被输出。值得注意的是，MH-GAN 不需要真实的样本进行初始化，只需要它所对应的判别器分数即可。

3. 校准

实际上，得到完美的 D 是不可能的，但是通过校准步骤可以达到相对完美的程度。另外，完美判别器的假设也不一定就真如它看起来那么好用。因为判别器仅对生成器和最初的真实数据进行评价，它只需要对来自生成器和真实数据分布的达到精确判别就可以。在一般的 GAN 训练中，一般不需要严格的要求判别器 D 的值达到一个确定的边界。但是 MH 算法需要从概率密度比方面对这个值进行良好的校准，从而得到正确的接受比。MH-GAN 使用 10% 的训练数据作为随机测试集，使用保序回归的方法对判别器 D 进行调整。

1D 和 2D 高斯结果

Uber 在论文中使用了一些小例子对 MH-GAN 和 DRS 方法进行了比较，其中真实数据来源于四个单变量的高斯模型的混合结果。通过 pG 的概率密度图可以看出普通的 GAN 存在的通病，它们的生成结果都缺失了一种模式（如图 4 所示）。但是，不使用γ校正 DRS 和 MH-GAN 则能良好的还原混合模型，而使用γ进行调整的 DRS 不能还原原始分布。然而，与使用γ进行调整的 DRS 方法相比，不使用γ的 DRS 方法在第一次接受之前抽样的数量增加了一个数量级。

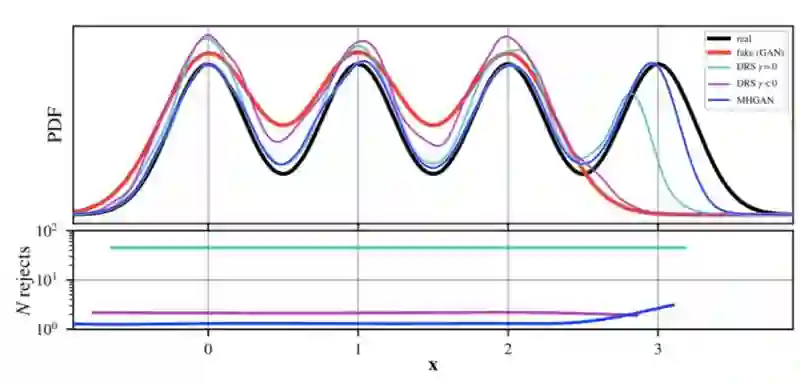
图 4：图中真实数据来自于四个高斯模型组成的 GMM，可以看出生成器的概率密度分布确实了一个模式。MH-GAN 和不使用γ的 DRS 能够产生该模式，尽管在第一次接受之前后者需要大量的抽样数据。

大部分文献（https://arxiv.org/abs/1606.00704）都喜欢用 5*5 的 2D 高斯模型作为一个简单的例子进行简单演示，Uber 也使用了这样的 2D 模型对基础 GAN、DRS、MH-GAN 在不同训练阶段下的情况进行了比较，如图 5 所示。所有的方法都采用了一个 4 层全连接卷积神经网络，使用线性整流函数（ReLU）作为激活函数，以及一个 100 维的隐层和一个维度为 2 的噪声向量。从视觉效果上来讲，相较于基础 GAN 的 DRS 取得了明显的提升，但是它的结果还是更接近基础 GAN 而不是真实数据。MH-GAN 可以模拟出所有 25 种模式并且从视觉效果上来讲更接近于真实数据。定量角度讲，MH-GAN 相较于其他方法具有更小的 JS 散度。

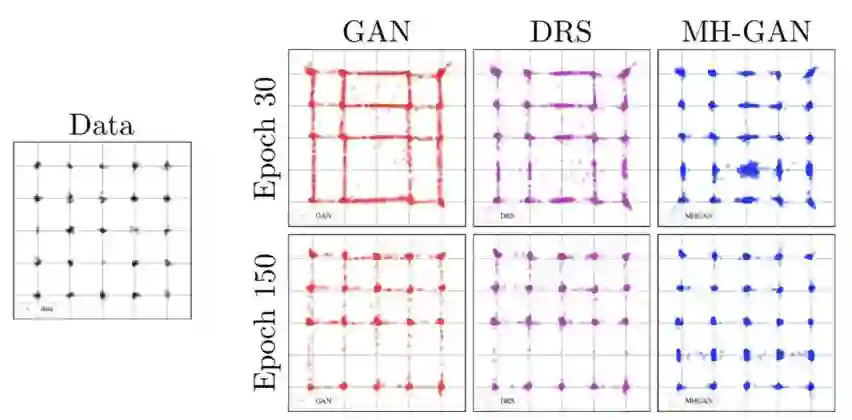
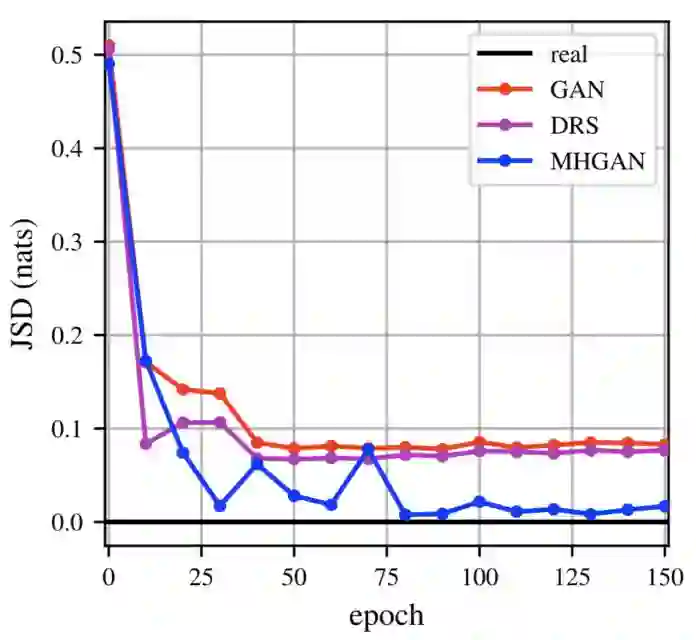
图 5：上图是 25 种高斯模型的 2D 分布情况。相较于基础 GAN，尽管 DRS 的样本点更集中于模式周围，但它缺失的一些模式上看起来与前者很相似，而 MH-GAN 则与真实数据更为相似。下图展示 MH-GAN 具有更小的 JS 散度。

在 CIFAR-10 和 CelebA 上的结果

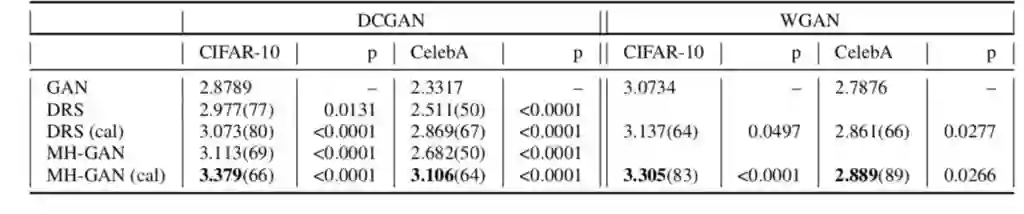
这部分内容主要展示了 MH-GAN 在真实数据上的效果，分别测试了选取使用了梯度惩罚的 DCGAN 和 WGAN 作为基础 GAN 的结果。在图 6 的表格中展示了校准后的 MH-GAN 的感知分数（Inception Socre）。

感知分数会完全忽略真实数据而只是用生成的图像进行评价，它需要将生成图像传入在 ImageNet 上预训练好的感知分类器中，感知分数会对输入图像属于某个详细类的置信度和预测类别的多样性进行测量。尽管感知分数存在缺陷，但它仍被广泛用于与其他工作进行比较。

基本上校准后的 MH-GAN 比其他方法都可以取得更好的效果，但是在整个训练过程中这种优势并不是一直存在的。对于这种情况的一个解释是，对于某一轮的迭代，判别器的分数与理想的判别器分数存在巨大差异，从而导致了接受概率缺乏准确性。

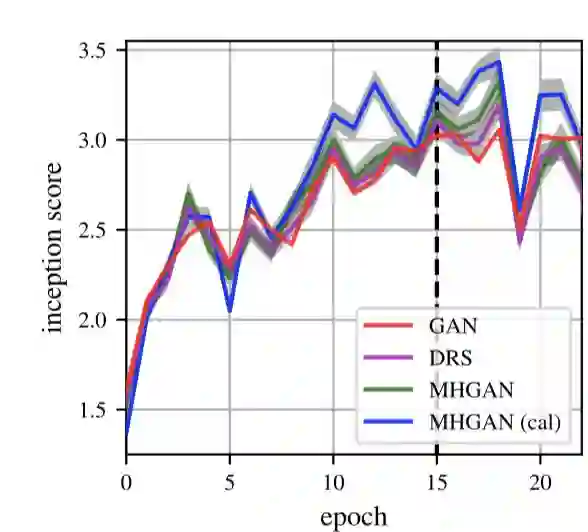
图 6：在 CIFAR-10 和 CelebA 上的感知分数，值越高表示效果越好。表格中的数据是第六十次迭代后的结果。

未来工作

MH-GAN 是一种提升 GAN 生成器的简单方法，该方法使用 Metropolis-Hastings 算法作为一个后处理步骤。在模拟数据和真实数据上 MH-GAN 都表现除了超越基础 GAN 的效果，与最近提出的 DRS 方法相比 MH-GAN 也更具有优势。目前该方法仅在较小的数据库和网络上进行了验证，下一步 Uber 计划将该方法用于更大的数据库和更先进的网络。将 MH-GAN 方法扩展到大规模数据库和 GAN 的途径是非常简单粗暴的，因为仅需要额外提供判别器分数和生成器产生的样本就可以！

此外，使用 MCMC 算法提升 GAN 的思想也可以扩展到其他更高效的算法上，例如汉密尔顿蒙特卡洛方法。如果想获取关于 MH-GAN 的更多细节和图表可以阅读论文：Metropolis-Hastings Generative Adversarial Network（https://arxiv.org/abs/1811.11357），如果想复现该工作，Uber 提供了该方法基于 Pytorch 的开源代码（https://github.com/uber-research/metropolis-hastings-gans）。

阅读原文：https://eng.uber.com/mh-gan/