【机器学习】Adaboost
本文介绍了集成学习中Boosting的代表算法Adaboost。首先介绍了Adaboost的Boosting思想:1)学习器的投票权重,2)更新样本权重,巧妙之处在于这两个权重的设计使得Adaboost如此优美。然后介绍了Adaboost的前向加法思想,即不断拟合上一次分类器的损失。最后以前向加法模型中的特例(二分类)导出Adaboost的指数损失理解,再次回归到Adaboost的学习器权重和样本更新权重为何如此设计。
作者 | 文杰
编辑 | yuquanle
Adaboost
Adaboost的Boosting理解
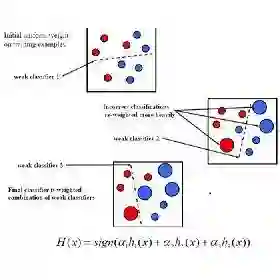
Adaboost是集成学习中Boosting方式的代表。多个基学习器其串行执行,下一个学习器基于上一个学习器的经验,通过调整样本的权重,使得上一个错分的样本在下一个分类器更受重视而达到不断提升的效果。
Adaboost集成多个学习器的关键在两点:
-
设置基学习器的权重:
-
调整样本的权重:
相对随机森林的Bootstrap Sampling重采样技术,可以看出Adaboost的权重调整是有目的性,基于上一个学习器的经验,这也导致Adaboost在基学习器层是串行的。值得探讨的是权重为何如此设置?
Adaboost算法采用的基学习器是二值函数(二叉树)模型,当然Adaboost的核心是采用Boosting的思想。
下面先来看Adaboost算法的整个流程,后面分析Adaboost在设计上巧妙之处。
-
输入:训练集:
-
输出:强学习器
-
初始化权值 :
,
-
训练M个基学习器 :
2.1 使用权值分布 与相应的基学习器算法得到第 个基学习器:
2.2 计算基学习器 的训练误差:
2.3 计算基学习器的权重:
如果 : ,舍弃基学习器,样本权重更新与不更新一致;
否则: ;
2.4 更新样本的权重:
其中:
这里 是归一化因子:
使得 满足一个概率分布;
-
得到 个基学习器之后,将基学习器线性组合:
-
得到最终的分类器:
Adaboost算法流程基本与Boosting思想一致,特别之处在于权重的设计,下面分析一下:
-
基学习器的权重 ,当 , ,且 随 的减小而增大,也就是说当基学习器的误差越小,权重越大。
-
样本权重更新公式可以表示如下:
也就是说正确分类 ,那么 ,正确分类的样本权重在上一次的基础上乘上一个小于1的因子而减小,反之,错分的样本的权重增大。
-
个基学习器在线性组合时,需要注意的是 ,最终的 是一个 区间的值,符号决定分类,绝对值表示分类一个确信度。
Adaboost的指数损失理解
Adaboost算法是前向分步加法算法的特例,以模型为加法模型,损失函数为指数函数的二类分类学习方法。考虑加法模型(additive model)
其中, 为基函数, 为基函数的参数, 为基函数的权重,显然这是一个加法模型。
在给定训练集和损失函数 的条件下,学习加法模型 就是最小化损失函数的问题:
当然,我们可以将加法模型看作一个复合函数,直接优化各个系数和基函数参数,但这样问题就变复杂了。
考虑前向分步算法,逐个优化每一个基函数和系数来逼近复合函数,这样问题就简化了。
具体的,每一步需要优化如下目标函数:
按照这种分步策略,每步优化一个基函数和系数,我们有前向分步算法如下:
-
输入:训练集:
-
输出:加法模型
-
初始化
-
学习 基函数和系数,从
2.1 极小化损失函数:
2.2 更新:
-
得到最终的加法模型:
前向分步算法通过逐个优化基函数,逐渐弥补残差的思想完成 个基函数的学习。
回到Adaboost算法,Adaboost是前向分步加法模型的特例。特例在于Adaboost是二分类,且损失函数定义为指数损失和基函数定义为二分类函数。
-
指数损失函数:
-
基函数:
在Adaboost算法中,我们最终的强学习器为:
以第 步前向分步算法为例,第 个基函数为:
其中 为:
根据前向分步算法得到 和 使得 在训练集 上的指数损失最小,即:
其中
由
这也就是样本权重更新的表达式(未归一化)。
现在分析目标函数,首先看 ,因为 , ,要使目标函数取到最小值,那么必然有:
也就是说 是第 步使得样本加权训练误差最小的基分类器。将 带入目标函数有:
上式对 求导即可,使得倒数为 ,即可得到 :
其中 是第 个基分类器 的分类错误率:
最后来看Adaboost的权重调整,都是前向分步算法基于一个目标:
可见一切设计都不是偶然,都是必然。Adaboost只是前向分步加法模型的特例,是GBDT的二分类特例,采用牛顿法求解版。
代码实战
vector<int> Classify(const Data data, int axis, double threshVal, string threshIneq){vector<int> label;for(size_t i=0; i<data.size(); i++){label.push_back(1);if(threshIneq=="lt"){if(data[i][axis]<=threshVal)label[i]=-1;}else{if(data[i][axis]>threshVal)label[i]=-1;}}return label;}Stump buildStump(const Data &data,vector<double> weight){Stump stump;int i,j,k,l;double *errArr=(double *)malloc(sizeof(double)*data.size());double minErr=MAX;double weightError=0;double *range=(double *)malloc(sizeof(double)*2);double rangemin,rangemax;double stepSize;int numSteps=data.size()/10;double threshVal;int label_index=data[0].size()-1;vector<int> label;string threshIneq[2]= {"lt","gt"};for(i=0; i<data[0].size()-1; i++) //属性{range=rangeSize(data,i);rangemin=range[0];rangemax=range[1];stepSize=(rangemax-rangemin)/numSteps;for(j=0; j<=numSteps; j++) //其实是numstep+1步{threshVal=rangemin+stepSize*j;for(k=0; k<2; k++) //大于小于{label=Classify(data,i,threshVal,threshIneq[k]);weightError=0;for(l=0; l<data.size(); l++){errArr[l]=label[l]-data[l][label_index]>0?(label[l]-data[l][label_index])/2:-(label[l]-data[l][label_index])/2;weightError+=errArr[l]*weight[l];}if(weightError<minErr){minErr=weightError;for(l=0; l<data.size(); l++){if(label[l]>0)stump.twosubdata.left.push_back(data[l]);elsestump.twosubdata.right.push_back(data[l]);}stump.label=label;stump.bestIndex=i;stump.minErr=minErr;stump.threshVal=threshVal;stump.ltOrgt=threshIneq[k];cout<<"minErr="<<minErr<<endl;stump.alpha=0.5*log((1-minErr)/minErr);}}}}return stump;}
完整代码见阅读原文
The End
推荐阅读
数学之美中盛赞的 Michael Collins 教授,他的NLP课程要不要收藏?
From Word Embeddings To Document Distances 阅读笔记
模型压缩实践系列之——bert-of-theseus,一个非常亲民的bert压缩方法
可解释性论文阅读笔记1-Tree Regularization
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLPer(id:ainlper),备注工作/研究方向+加群目的。