模型汇总19 强化学习(Reinforcement Learning)算法基础及分类
前一期介绍了强化学习基础知识,今天,主要介绍强化学习各种算法理论基础。处于一个state空间下,Agent一系列动作决策问题,类似于一个马尔科夫决策过程(Markov Decision Process, MDP),即当前的状态只与前一个状态有关,因此,Agent面临的其实是在某个状态State(环境下),一个最优动作(Action)序列的决策问题。动态规划和强化学习都是基于马尔科夫链,求解一个最优动作序列的方法。动态规划的方法主要解决当MDP环境下,Agent的状态转移概率和回报函数模型已知的决策问题;强化学习主要处理二者未知情况下,最优动作序列的决策问题。
1、马尔科夫决策过程(Markov Decision Process,MDP)概念
强化学习随机过程定义:
假设存在一个由{S,A,D,P,r,J}六元组描述的,与Agent决策有关的,离散时间随机决策过程,其中,S表示有限的环境状态空间,A表示有限的动作空间,D表示S的初始状态概率分布。P表示Agent的状态转移概率,属于[0,1],是P(s,a,s’)的简写,表示在状态s下,执行动作s,转移到状态s’的概率函数。R表示回报函数,是r(s,a,s’):S X A X S’的简写,表示Agent根据转移概率P(s,a,s’)动作后,Agent得到的立即回报(奖赏)函数。J表示动作序列决策的目标函数,因此,R是一种“短视”评价信号,J是一种“远视”评价信号。
马尔科夫性质:未来状态只与当前状态有关,与历史状态无关,即P(St+1|St)= P(St+1|S1,S2....St)。
马尔科夫性质的意义:当前状态S包含了历史Step的所有相关信息,且当前状态足够用于预测未来的状态,因此,只要当前状态,历史状态就可以抛掉。
马尔科夫过程或马尔科夫链定义:具有马尔科夫性质的随机过程,可以采用一个二元组<S,P>表示,其中S是一个有限的状态集合,P表示状态的转移概率(从一个状态s,转移到另一个状态s’的概率),Pss’=P(St+1=S’|St=S)。
Markov Reward Process(MRP)与Markov Decision Process(MDP)的联系与区别:
MRP是MDP的基础,MRP由<S,P,R,r>四元组构成,S、P、R与上面定义已知,分别表示随机过程的状态空间,转移概率矩阵和之间奖励函数,r表示折扣因子(后面会仔细讲)。
MDP是一个与决策相关的MRP过程,随机过程中所有状态都具有马尔科夫性质。MDP由<S,A,P,R,r>构成,比MRP多了一个A,表示随机过程中,有限的动作集合。
在基于马尔科夫过程的强化学习序列决策过程中,Agent从目前状态s调到下一个状态s’的转移概率P和立即回报R,只与当前的状态s有关,与历史的状态和动作无关,这样可以简化决策过程目标函数J的求解问题,也是Bellman方程的基础。比如,在马尔科夫决策过程环境下,状态转移概率求解可以大大简化:
P(S=St,A=At,S’=S(t+1))=Pr{S(t+1)|(St,At,St-1,At-1,.....S0,A0)}=Pr{St+1|St,At}
马尔科夫决策环境下,动作序列决策过程的目标函数J有三种表示形式,即有限序列总回报目标函数、无限序列折扣总回报目标函数和有限序列平均回报目标函数。
有限总回报目标函数为:
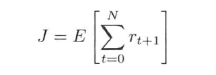
(1)
其中,rt表示t时刻的立即回报,N表示序列长度,即马尔科夫链长度。
无限折扣总回报目标函数:
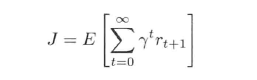
(2)
其中,tao属于(0,1]表示折扣因子。
有限序列平均回报目标函数:
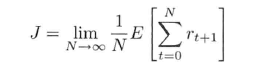
(3)
在MDP决策过程中,一般都采用无限折扣回报目标函数和有限平均回报目标函数求解J。为什么?因为实际情况下,大多数的马尔科夫Reward和决策过程都是包含折扣的,这样做具有以下优点:
(1)、方便计算打折后的Reward,与实际情况相符。
(2)、避免出现无限循环的马尔科夫决策过程。
(3)、把直接回报(immediate reward)R与未来回报(delayed reward)区分开来,直接回报影响更大,符合人或动物倾向于选择直接回报实际情况。
(4)、描述了我来回报对于总回报影响的不确定性。
此外,可以发现,平均回报是折扣回报一个特例,当折扣回报目标函数中的折扣因子取值为1时,两个目标函数等价。
2、策略、值函数和Bellman方程
策略(policy)pi:S -> A -> [0,1],确定了Agent在状态S下,选择动作A的概率。在MDP环境下,当策略确定后,MDP对应的值函数(value function)可以分为:只与状态有关的状态值函数Vpi(s),与状态->动作相关的动作值函数Qpi(s,a)。与直接回报R不同,值函数(状态值函数V或动作值函数Q)是对未来回报函数的一种预测,目的是为了获得更多的回报。因此,Agent进行动作选择时,不是根据直接回报R进行选择,而是根据值函数回报进行选择。
状态值函数Vpi(s)对应的是一个马尔科夫奖直接奖励过程(Markov Reward Process, MRP),描述值函数的值,仅有当前和未来的直接Reward相关,与动作无关。状态值函数表达式如公式(4)所示:
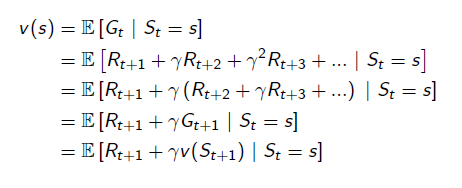
(4)
状态值函数表示Agent从状态s开始,根据策略pi选择动作所获得的期望总回报。P(.)和R(.)分别表示对应的转移概率和回报函数。
公式(4)也是著名的Bellman方程。值函数Vpi(St)的值可以被分成两个部分:直接回报r(t+1)和折扣的未来回报rV(St+1),因此,可以按照状态序列对值函数进行拆解,通过迭代求和方式得到值函数V(s)的值。
基于Bellman方程求解状态值函数V(s)的值:
把值函数的表达式简化,可以得到简化的Bellman方程表达式:
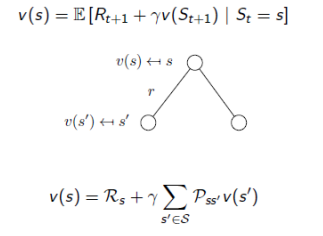
图中,V(s)对应公式(4)中Vpi(s),表示当前状态的值函数,V(s’)对应公式V(St+1)。状态值函数可以看做与转移概率矩阵Pss’和直接回报Rs相关的线性防长,在状态转移矩阵和直接回报已知条件下,很容易求解状态值函数的值。对于比较短的MRP过程的状态值函数,可以直接计算V(s)的值。但对于比较长的MRP过程状态值函数求解,一般还是通过迭代方法求解,如:动态规划方法(Dynamic Programming)、蒙特卡洛方法(Monte-Carlo Evaluation)、时间差分学习(TD Learning)方法。
动作值函数Qpi(s,a)对应的是一个MDP过程。类似于状态值函数,动作值函数Qpi(s,a)表示agent从状态s、动作a出发,根据策略pi进行动作选择,所获得的期望回报,表达式如(5)所示:
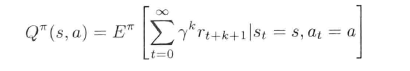
(5)
动作值函数同样也满足Bellman方程,其Bellman方程公式(6)所示:
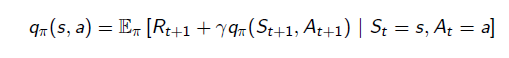
状态值函数V(s)与动作值函数Q(s,a)之间关系:
根据Bellman方程,
对于一个确定性策略pi,V(s)=Q(s,pi(s))。
对于随机性的策略pi,V(s)=E(pi(s,a) * Q(s,a)),其中E(.)表示累加求和,如下图所示。
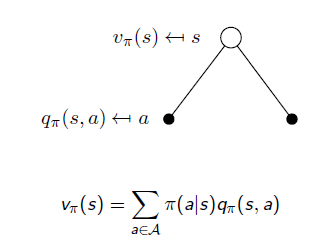
因此,对于一个策略,无论是否随机,动作值函数和状态值函数之间存在公式(7)所示关系:
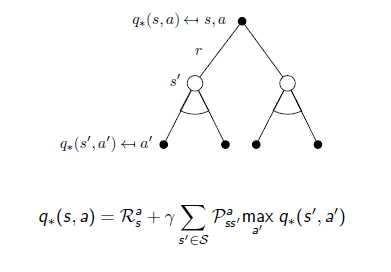
(7)
3、最优值函数、最优策略的定义和求解:
最优值函数定义:对于所有的状态值函数V(s)和动作值函数Q(s,a)都存在一个最优的值函数V*和Q*,使得两个值函数的值达到最大,即:V(s)*=MAXpi(V(s)),Q(s,a)=MAXpi(Q(s,a))。MDP的求解过程,就是在寻找最优的值函数,因为,最优的值函数表示MDP过程最优状态。
最优策略定义:最优值函数对应的策略为最优策略pi*,对于任意策略pi,pi* >= pi,此时,V(s)* = Vpi*(s),Q(s,a)* = Qpi*(s,a)。
根据Bellman方程求解最优值函数:
Bellman最优值状态值函数:
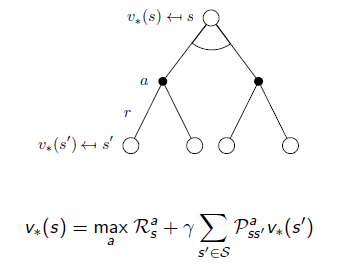
(8)
Bellman最优最优动作值函数:
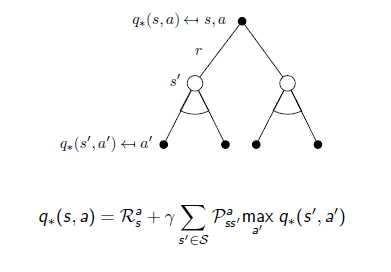
(9)
可见,可以通过迭代的方法求解MDP过程的最优值函数,迭代的方法有:值迭代(Value iteration),策略迭代(Policy Iteration),Q-学习,Sarsa算法。
4、强化学习常用算法分类
1)、模型已知(Model Based)的动态规划方法
在模型已知的MDP情况下,MDP的状态转移概率和回报函数已知,此时,可以采用动态规划的方法来寻找最优的策略。常用的动态规划方法有四种:
(1)、线性规划方法。根据Bellman方程,将值函数的求取转换为一个线性规划问题求解。
(2)、策略迭代方法。根据Bellman方程,通过策略迭代和策略评估交替进行,求取最优策略。
(3)、值函数迭代方法。通过一种逐次逼近方式,将有限时段的动态规划算法推广到无限时段上。
(4)、广义策略迭代方法。结合策略迭代和值迭代的一种强化学习方法。
2)、模型未知(Model Free)的强化学习方法包括:蒙特卡洛学习、TD学习、Q学习、SARSA学习、Dyna框架、直接策略学习和Actor-Critic方法,并给出了相应的流程图。
3)、近似强化学习的基本方法,包括带值函数的TD学习、近似值迭代、近似策略迭代和最小二乘策略迭代。
往期精彩内容推荐:
模型汇总-12 深度学习中的表示学习_Representation Learning



DeepLearning_NLP


深度学习与NLP

欢迎访问个人CSDN账号:lqfarmer