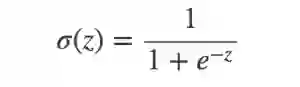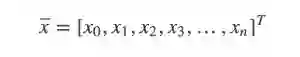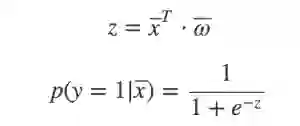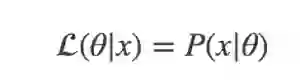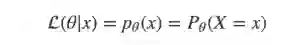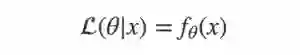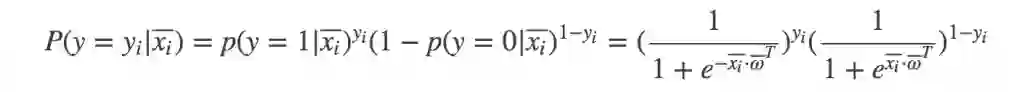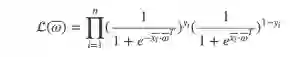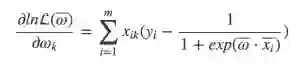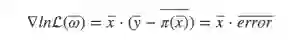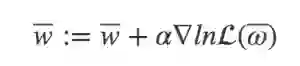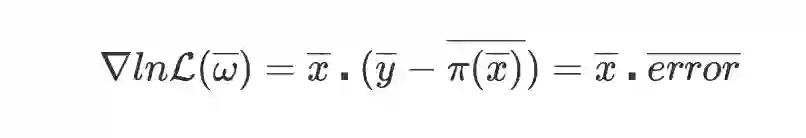机器学习算法实践：Logistic 回归与梯度上升算法

2017 年 7 月 30 日 Python开发者

（点击上方蓝字，快速关注我们）

来源：伯乐在线专栏作者 - iPytLab

如有好文章投稿，请点击 → 这里了解详情

前言

关于Logistic回归分类器主要分两部分进行总结，第一部分主要介绍Logistic回归的理论相关的部分，涉及到通过似然函数建立Logistic回归模型以及使用梯度上升算法优化参数。第二部分主要使用Python一步步实现一个Logistic回归分类器，并分别使用梯度上升和随机梯度上升算法实现，对二维数据点分类进行可视化，最后使用之前使用过的SMS垃圾短信语料库中的短信数据进行模型训练并对短信数据进行分类。

Logistic回归

Logistic回归为概率型非线性回归模型, 是研究二值型输出分类的一种多变量分析方法。通过logistic回归我们可以将二分类的观察结果y与一些影响因素[x1,x2,x3,…]建立起关系从而对某些因素条件下某个结果发生的概率进行估计并分类。

Sigmoid函数

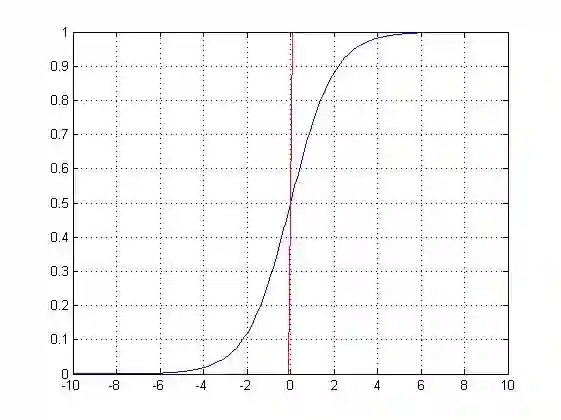
对于二分类问题，我们想要一个函数能够接受所有输入然后预测出两种类别，可以通过输出0或者1。这个函数就是sigmoid函数，它是一种阶跃函数具体的计算公式如下:

Sigmoid函数的性质: 当x为0时，Sigmoid函数值为0.5，随着x的增大对应的Sigmoid值将逼近于1; 而随着x的减小, Sigmoid函数会趋近于0。

Logistic回归分类器(Logistic Regression Classifier)

Logistic回归分类器是这样一种分类器:

在分类情形下，经过学习后的LR分类器是一组权值

样本也可以用一组向量 x 表示:

其中x0=1

将 x 根据 w 线性叠加带入到Sigmoid函数中便可以得到范围在 (0,1), 之间的数值，大于0.5被分入1类，小于0.5的被归入0类:

其中p(y=1|x)就是指在特征为x属于类1的条件概率, 当然也可以容易得到属于类0的概率为:

所以Logistic回归最关键的问题就是研究如何求得 ω 。这个问题就需要用似然函数进行极大似然估计来处理了。

似然函数(Likelihood function)

In statistics, a likelihood function (often simply the likelihood) is a function of the parameters of a statistical model given data.

从似然函数的英文定义中可以看到，似然函数是与统计模型中的参数的函数。虽然似然性和概率的意思差不多，但是在统计学中却有着明确的区分:

概率(Probability)使我们平时用的最多的，用于在一直某些参数的值的情况下预测某个事件被观测到的可能性。

似然性(Likelihood)则是在一直观测到的结果时，对有关参数进行估计。
可见这两个是个概念是个可逆的过程，即似然函数是条件概率的逆反.

对于某个已发生的事件 x, 某个参数或者某个参数向量 θ 的似然函数的值与已知参数 θ 前提下相同事件 x 放生的条件概率(概率密度)的值相等, 即:

似然函数对于离散和连续随机分布的表示形式是不同的:

离散型

对于具有与参数 θ 相关离散概率分布 p 的变量 X, 对于某个变量 X=x θ 的似然函数表示成:

连续型

连续性的分布我们则用概率密度 f 来表示:

注意似然函数并不是一个条件概率，虽然表达式与条件概率的形式相同。因为 θ 并不是一个随机变量而是一个参数。

关于对似然性的理解，个人认为，似然性并不是一个概率，而是表示在一些列事件发生时，关于事件相关的参数的可能性信息，一个参数就对应一个似然函数的值，当参数发生变化的时候，似然函数也会随之变化，似然函数的重要性并不在于他的具体值是多少，而在于他随参数变化的变化趋势，是变大还是变小。当我们在取得某个参数的时候，似然函数的值到达了极大值，则说明这个参数具有**最合理性**。

极大似然估计

极大似然估计是似然函数最初也是最然的应用，我们优化Logistic模型就行极大似然估计的过程(求似然函数的极大值)，通过极大似然估计，我们可以得到最合理的参数。

Logistic回归中的极大似然估计

上一部分总结了什么似然函数和极大似然估计，这里就总结下Logistic模型的极大似然估计。

在LR分类器部分我们推导了Sigmoid函数计算两类问题的概率表达式，由于是二分类，分类结果是0和1，我们可以将两种类别的概率用一个式子表达, 对于一个样本 xi 得到一个观测值为 yi 的概率为:

若各个样本之间是相互独立的，则联合概率为各个样本概率的乘积。于是根据这系列的样本，我们就能得到关于参数向量 ω 的似然函数 L(ω) :

我们的目的就是要对这个似然函数的极大值进行参数估计，这便是我们训练Logistic回归模型的过程。通过极大似然估计我们便可以通过所有样本得到满足训练数据集的最合理的参数 ω

通过梯度上升算法进行极大似然估计

有了似然函数，我们便可以通过优化算法来进行优化了。使用梯度上升需要计算目标函数的梯度，下面我简单对梯度的计算进行一下推导:

为了方便，我们将似然函数取自然对数先,

然后我们对去过对数的函数的梯度进行计算:

通过矩阵乘法直接表示成梯度:

设步长为α, 则迭代得到的新的权重参数为:

这样我们通过梯度上升法做极大似然估计来做Logistic回归的过程就很清楚了，剩下的我们就需要通过代码来实现Logistic回归吧.

Python实现

前面主要总结了Logistic回归模型建立的理论基础，主要包含模型似然函数的建立以及梯度上升算法的优化推导。下面我们在上文的基础上使用Python一步步实现一个Logistic回归分类器。

加载数据

从文件中读取特征以及类别标签用于优化模型参数

def load_data(filename):

    dataset, labels = [], []

    with open(filename, 'r') as f:

        for line in f:

            splited_line = [float(i) for i in line.strip().split('\t')]

            data, label = [1.0] + splited_line[: -1], splited_line[-1]

            dataset.append(data)

            labels.append(label)

    dataset = np.array(dataset)

    labels = np.array(labels)

    return dataset, labels

使用梯度上升算法

上文对Logistic回归模型使用梯度上升算法优化参数进行了理论介绍，这里就最先使用梯度上升算法来构建一个分类器.

首先我们是Sigmoid函数:

def sigmoid(x):

    ''' Sigmoid 阶跃函数

    '''

    return 1.0/(1 + np.exp(-x))

然后是梯度上升算法的实现:

def gradient_ascent(self, dataset, labels, max_iter=10000):

    ''' 使用梯度上升优化Logistic回归模型参数

    :param dataset: 数据特征矩阵

    :type dataset: MxN numpy matrix

    :param labels: 数据集对应的类型向量

    :type labels: Nx1 numpy matrix

    '''

    dataset = np.matrix(dataset)

    vlabels = np.matrix(labels).reshape(-1, 1)

    m, n = dataset.shape

    w = np.ones((n, 1))

    alpha = 0.001

    ws = []

    for i in range(max_iter):

        error = vlabels - self.sigmoid(dataset*w)

        w += alpha*dataset.T*error

        ws.append(w.reshape(1, -1).tolist()[0])

    self.w = w

    return w, np.array(ws)

在这里的数据操作都转换成Numpy矩阵的操作，主要是方便处理避免Python循环处理。同时每次梯度上升迭代过程中都把自变量，也就是Logistic模型参数进行收集，方便最后查看参数收敛情况。

关于梯度上升算法中，我们每次沿着梯度方向移动的步长 αα 都设的固定距离为0.001，并没有做一维搜索。

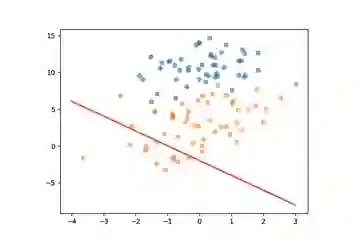
可视化决策边界

Sigmoid函数的特点就是通过0点来进行分类，xT⋅ω 的值小于0为一类，大于0位另外一类，因此我们可以通过 xT⋅ω=0 来获取分界线或者超平面。在二维平面里，我们可以通过求解 w0x0+w1x1+w2x2(其中 x0=1) 并绘制直线来可视化决策边界。

def snapshot(w, dataset, labels, pic_name):

    ''' 绘制类型分割线图

    '''

    if not os.path.exists('./snapshots'):

        os.mkdir('./snapshots')

    fig = plt.figure()

    ax = fig.add_subplot(111)

    pts = {}

    for data, label in zip(dataset.tolist(), labels.tolist()):

        pts.setdefault(label, [data]).append(data)

    for label, data in pts.items():

        data = np.array(data)

        plt.scatter(data[:, 1], data[:, 2], label=label, alpha=0.5)

    # 分割线绘制

    def get_y(x, w):

        w0, w1, w2 = w

        return (-w0 - w1*x)/w2

    x = [-4.0, 3.0]

    y = [get_y(i, w) for i in x]

    plt.plot(x, y, linewidth=2, color='#FB4A42')

    pic_name = './snapshots/{}'.format(pic_name)

    fig.savefig(pic_name)

    plt.close(fig)

好了，优化算法和可视化代码都具备了，我们便可以拟合我们的数据了，这里使用两种类型的二维数据点来训练模型, 数据见https://github.com/PytLab/MLBox/blob/master/logistic_regression/testSet.txt

if '__main__' == __name__:

    clf = LogisticRegressionClassifier()

    dataset, labels = load_data('testSet.txt')

    w, ws = clf.gradient_ascent(dataset, labels, max_iter=50000)

    m, n = ws.shape

    # 绘制分割线

    for i in range(300):

        if i % (30) == 0:

            print('{}.png saved'.format(i))

            snapshot(ws[i].tolist(), dataset, labels, '{}.png'.format(i))

    fig = plt.figure()

    for i in range(n):

        label = 'w{}'.format(i)

        ax = fig.add_subplot(n, 1, i+1)

        ax.plot(ws[:, i], label=label)

        ax.legend()

    fig.savefig('w_traj.png')

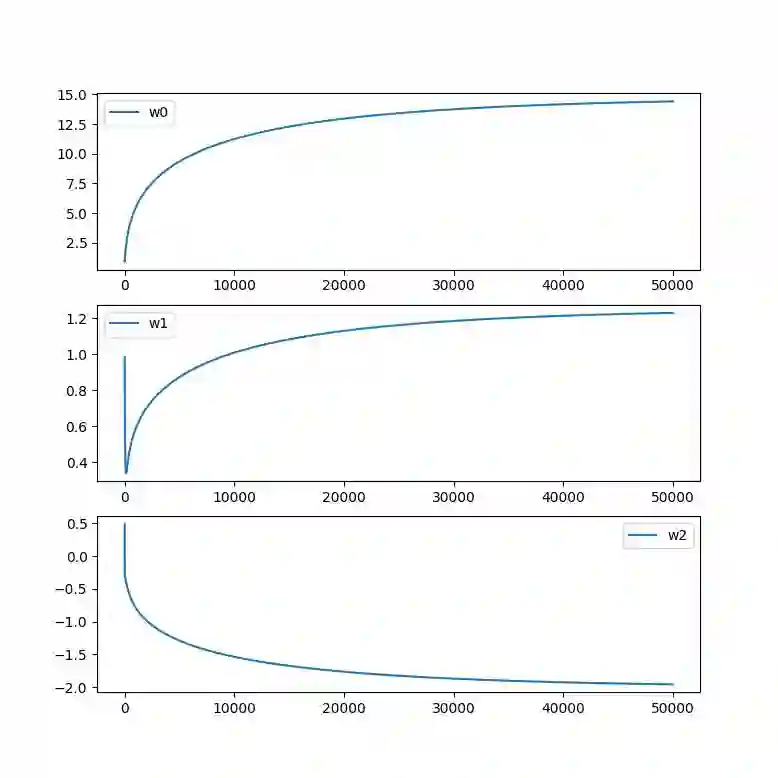
通过将迭代过程中的权重参数输出，我们可以绘制决策边界的变化，看到参数的优化过程:

下面我们可视化一下模型参数在梯度上升过程中的收敛情况，我们总共迭代了50000步：

使用随机随机梯度上升算法

从求目标函数梯度的公式

和实现代码

error = vlabels - self.sigmoid(dataset*w)

w += alpha*dataset.T*error

中我们可以看到，在使用梯度上升算法优化的时候每次迭代都需要使用所有的训练数据乘上误差向量，如果样本只有几百个那还好，如果有数十亿样本，那这个矩阵乘法将会非常的大，于是我们可以考虑使用随机梯度上升来更新 ω , 所谓随机梯度就是指更新 ω 的时候不需要用所有的数据矩阵和误差矩阵乘积来更新，而是使用样本中随机选出的一个数据点来计算梯度并更新。这样可以在新的样本到来时对分类器进行增量式更新，因而随机梯度算法是一个在线学习算法, 之前的梯度上升算法是一次性处理所有样本数据被称作是批处理。

下面我们就重新写一个通过随机梯度上升算法优化的Logistic回归分类器

from logreg_grad_ascent import LogisticRegressionClassifier as BaseClassifer

from logreg_grad_ascent import load_data, snapshot

class LogisticRegressionClassifier(BaseClassifer):

    def stoch_gradient_ascent(self, dataset, labels, max_iter=150):

        ''' 使用随机梯度上升算法优化Logistic回归模型参数

        '''

        dataset = np.matrix(dataset)

        m, n = dataset.shape

        w = np.matrix(np.ones((n, 1)))

        ws = []

        for i in range(max_iter):

            data_indices = list(range(m))

            random.shuffle(data_indices)

            for j, idx in enumerate(data_indices):

                data, label = dataset[idx], labels[idx]

                error = label - self.sigmoid((data*w).tolist()[0][0])

                alpha = 4/(1 + j + i) + 0.01

                w += alpha*data.T*error

                ws.append(w.T.tolist()[0])

        self.w = w

        return w, np.array(ws)

我们写一个继承与刚才实现的分类器的派生类，并实现随机梯度算法，这里沿着梯度方向的步长随着迭代会逐渐减小来减弱参数的博定。

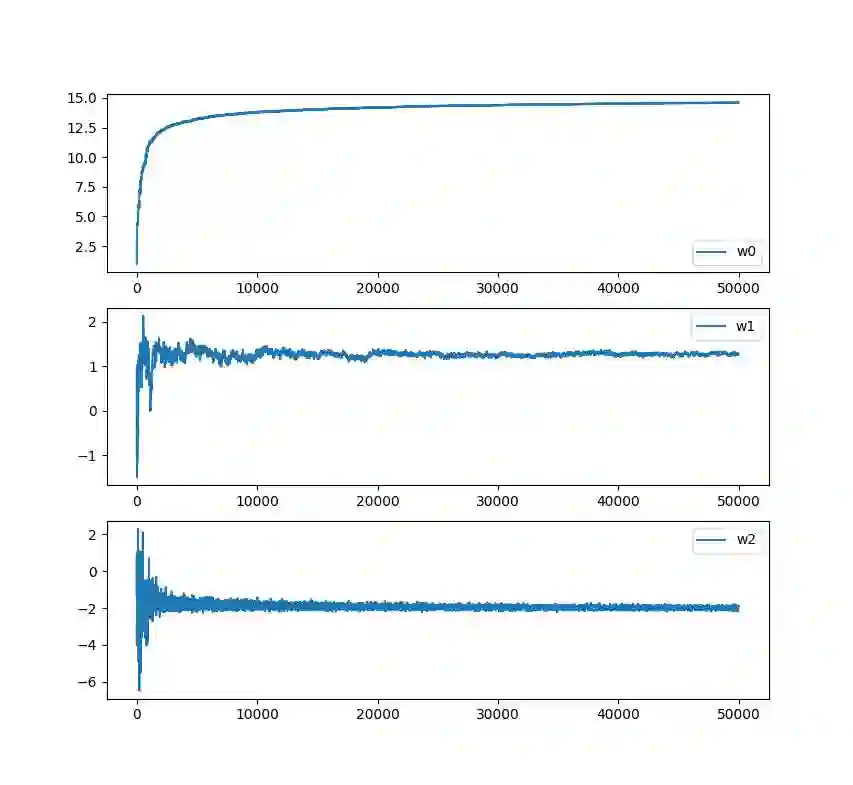
我们同样来可视化决策边界和参数的收敛曲线来看看随机梯度下降法对模型的优化过程:

if '__main__' == __name__:

    clf = LogisticRegressionClassifier()

    dataset, labels = load_data('testSet.txt')

    w, ws = clf.stoch_gradient_ascent(dataset, labels, max_iter=500)

    m, n = ws.shape

    # 绘制分割线

    for i, w in enumerate(ws):

        if i % (m//10) == 0:

            print('{}.png saved'.format(i))

            snapshot(w.tolist(), dataset, labels, '{}.png'.format(i))

    fig = plt.figure()

    for i in range(n):

        label = 'w{}'.format(i)

        ax = fig.add_subplot(n, 1, i+1)

        ax.plot(ws[:, i], label=label)

        ax.legend()

    fig.savefig('stoch_grad_ascent_params.png')

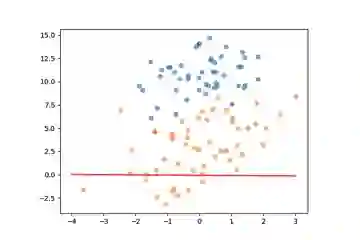
决策线变化:

参数收敛曲线:

使用Logistic回归分类器分类短信

这里我还是使用了前两篇决策树和贝叶斯分类器使用的垃圾短信数据集来训练Logistic回归分类器，这时候对于Logistic分类器的参数可能会比较多，我们使用随机梯度上升算法来优化参数，相对于贝叶斯分类器，基于随机梯度上升算法的Logistic回归分类器对于维数较高的的数据向量和数量较大的数据集的训练速度还是有待改善的，我们同样使用留存交叉验证的方式来训练和测试模型，测试了三次Logistic回归模型对于垃圾短信的识别错误率分别为: 0.0833, 0.038, 0.038.