一文解读Tensor到底是个啥玩意儿？（附代码）

会员服务 ·

一文解读Tensor到底是个啥玩意儿？（附代码）

2018 年 6 月 13 日 数据派THU

作者：Matthew Mayo, KDnuggets.

翻译：和中华

校对：丁楠雅

本文约1000字，建议阅读5分钟。

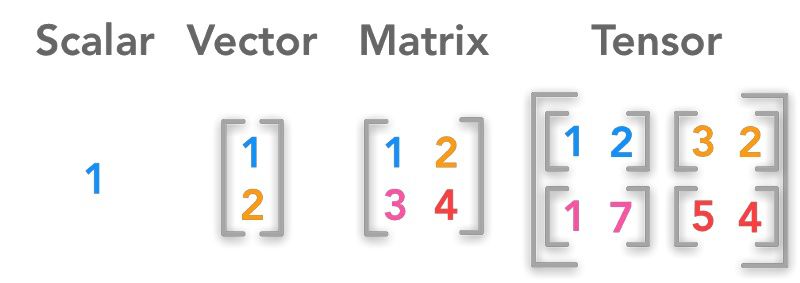
本文介绍了各种数值型数据的容器（标量、向量、矩阵、张量）之间的关系，在实践中，张量特指3维及更高维度的数据容器。

尽管理论上和实践中的张量（tensors）有一些细微差别，我们仍然能给出这样的定义：一个张量就是一个可以容纳N维数据及其线性操作的容器。

机器学习中的数据通常需要处理为数值型的。特别地，当我们特指神经网络中的数据表示时，通常会提到所谓的张量。一个张量就是一个可以容纳N维数据的容器。很多时候，人们会把它和matrix错误地混用（matrix特指2维的张量），张量是matrix在N维空间的一般形式。

数学上讲，张量不仅仅是一个数据容器，除了保存数值型数据，它也包括张量之间合法的线性变换。这种变换的例子如：叉积（cross product）和点积（dot product）。从计算机科学的角度看，把张量理解成面向对象中的对象而不是简单的一个数据结构会更有帮助。

（译者注：因为作者提到张量不仅包含数据，而且包含相应的操作，这与我们在面向对象编程中的约定是一致的，所以作者更建议理解成是对象。）

虽然上面的描述都是正确的，但理论上和机器学习实践中所指的张量还是会有细微差别。我们暂时简单地将他们视为数据结构，下图概括了张量和标量、向量跟矩阵的关系，以及如何用Numpy创建各种数据类型的代码。在随后的帖子中我们还会看看张量的变换。

标量

单个数字就是一个标量。标量是一个0维的张量。因此，它具有0个轴，并且秩为0。

这就是细微差别出现的地方，尽管单个数字可以表示为张量，但并不是说它就应该是张量或者通常是张量。我们有足够的理由把数字视为张量（讨论张量的操作时会看到），但作为一种存储机制，这种表示会让人困惑。

下面的代码中，Numpy的多维数组ndarray被用来创建刚才讨论的示例结构。回忆一下，多维数组的ndim属性返回数组的维数。

import numpy as np

x = np.array(42)

print(x)

print('A scalar is of rank %d' %(x.ndim))

42

A scalar is of rank 0

向量

向量是1维的张量，在计算机科学中经常把它叫做数组。向量由一串数字组成，具有1个轴，并且秩为1。

x = np.array([1, 1, 2, 3, 5, 8])

print(x)

print('A vector is of rank %d' %(x.ndim))

[1 1 2 3 5 8]

A vector is of rank 1

矩阵

矩阵是秩为2的张量，即它有两个轴。在各种场景你都能熟悉这个概念，尤其是把数据喂给你的scikit-learn机器学习模型时。矩阵就是把数字放入网格内（想象行和列），是一个2维的张量。

x = np.array([[1, 4, 7],

[2, 5, 8],

[3, 6, 9]])

print(x)

print('A matrix is of rank %d' %(x.ndim))

[[1 4 7]

[2 5 8]

[3 6 9]]

A matrix is of rank 2

三维张量(及更高的维度)

严格来说，上述结构都是合法的张量。通常谈到张量时，都是将矩阵的概念推广到N>=3维。为了避免混淆，我们通常只把3维或更高维度的张量称为张量（通常而言，把标量‘42’称为张量没什么好处，只会让人困惑）。

x = np.array([[[1, 4, 7],

               [2, 5, 8],

               [3, 6, 9]],

              [[10, 40, 70],

               [20, 50, 80],

               [30, 60, 90]],

              [[100, 400, 700],

               [200, 500, 800],

               [300, 600, 900]]])

print(x)

print('This tensor is of rank %d' %(x.ndim))

[[[ 1   4   7]

  [ 2   5   8]

  [ 3   6   9]]

[[ 10 40 70]

  [ 20 50 80]

  [ 30 60 90]]

[[100 400 700]

  [200 500 800]

  [300 600 900]]]

This tensor is of rank 3