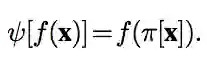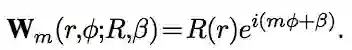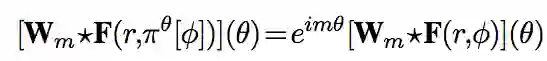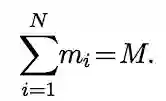H-Nets:让CNN的旋转等变性更加稳定
编者按:近日国外网友扒出了去年CVPR中的优秀论文Harmonic Networks: Deep Translation and Rotation Equivariance,这篇来自UCL的研究成果介绍了一种改良过的神经网络,它可以清晰地辨认平移过旋转360°的图形以及边界,等变性结果比传统CNN要好得多。以下为论智对该成果的编译。
在计算机视觉任务中,图像的平移或旋转不应该影响结果。卷积神经网络具有平移等变性:输入平移过的图像,结果会生成相对应的特征映射。但是对于旋转的图像就不是这么容易了,如果一个人向CNN中输入一个旋转后的图像,那么特征向量可能不会以有意义或容易预测的方式旋转。能直接将输入变换与特征向量变换联系起来的性质称为等变性(equivariance)。想实现全局旋转等变,通常选用data augmentation的方法,但是想分批进行等变处理就更加困难了。
在这篇论文中,我们提出了Harmonic Networks(H-Nets),可以批量处理平移和360°旋转的图像。我们用圆形谐波替换原来的CNN滤波器,然后在每个接受域返回最大的response。圆形谐波是可控滤波器,这意味着我们可以用有限的线性组合来表示所有旋转后的滤波器。这就解决了CNN中需要学习多个滤波器副本的问题,并且保证了旋转等变性,并能生成旋转图片可预测的特征映射。具体效果可戳视频感受一下。
问题分析
许多计算机视觉系统都在追求不受到其他因素的影响,例如目标物体识别或边界检测,它们都针对仿射变换有着不可变性。通过将CNN的卷积滤波器固定在圆形谐波族中,H-Nets将360°旋转的图像转换成它们的特征表示。接下来我们将大致解释三个概念:
等变性(Equivariance)
圆形谐波是如何做到旋转等变的
圆形谐波的特点,如何将其结合到CNN框架中
等变性
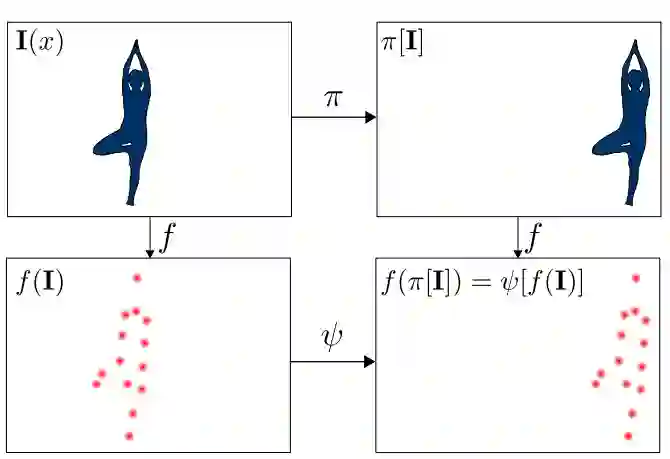
等变性是非常有用的属性,因为输入图像的变换π可以生成可预测的特征变换ψ,这些特征是可解释的,并且能让学习变得容易。用公式来表示,即如果我们可以将输入x∈X的每个变换π∈Π与ψ∈Ψ相关联,那么f:X→Y就等价于一组变换。即:
这意味着我们进行特征映射和变换的顺序就不重要了。
如上图所示,在CNN中,像素平移和特征映射的应用顺序是可以互换的。
复杂的圆形谐波
利用数据增强,CNN可能会学到一些旋转等变性,但是这很难量化。而H-Nets的方法更简单。如果f是一个标准的卷积层的特征映射,那么将滤波器固定在圆形谐波群中可以很好地解决360°旋转的问题。
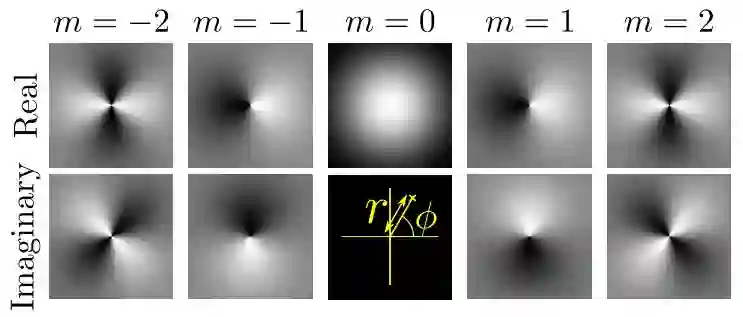
这里,r、φ是图像/特征映射的空间坐标,以极坐标的形式表示。m∈Z是旋转顺序,R:R+→R是一个方程,成为radial profile,控制滤波器的总体形状。β∈[0,2π)是一个相位偏移项,可以让滤波器选择方向。下图是一个示例:
复杂的高斯滤波器,不同的旋转顺序
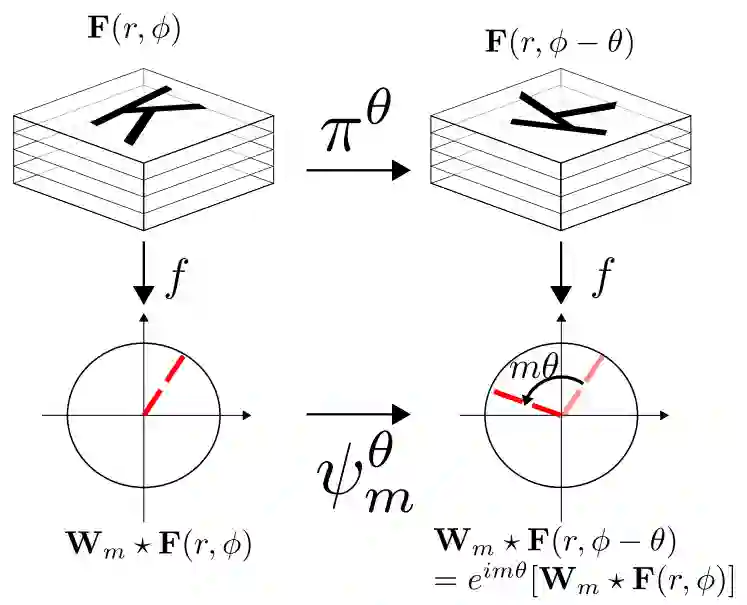
圆形谐波的旋转等变
假设将一个顺序为m的圆形谐波与旋转后的图像补丁相关联,补丁在原始滤波器处只能做局部旋转。这意味着互相关联的响应仅仅是输入图片补丁旋转θ的标量函数,并且这种响应很复杂。利用文中第一个公式,结合极坐标系,图像F(r,φ)对于原始滤波器旋转θ角度后得到的是F(r,φ−θ),所以旋转变换过程可以被写成F(r,πθ[φ])=F(r,φ−θ)。结果可以表示为:
这里Wm是Wm(r,φ;R,β)的缩写。
数学过程以及等变条件
圆形谐波的重要特征有三个:
旋转顺序m1和m2的相关性会生成新的旋转顺序m1+m2
点状非线性h:C→C,只控制旋转的尺度,所以我们可以将相关性加入适应了复杂域的CNN非线性。
顺序m下的两个响应也保持m的顺序。所以要创建一个CNN,其中的输出与输入的旋转是M对等的,我们需要:
实验方法
我们已经考虑了特征映射经过360°旋转后的图像,并且确定了旋转顺序。接下来我们将用这些结果构建一个深层次结构,它可以利用圆形谐波的等变特性。
特征映射和滤波器的旋转顺序之和具有相关性,所以为了在输出时得到一个既定的旋转顺序,我们必须遵守等变条件。网络中的每个特征映射都必须满足等变条件,否则就会生成带有两个通道的特征映射,最终的旋转顺序就不一样。针对这一问题,我们需要结合复杂的特征,以不同频率旋转图像,让每个特征映射都符合等变条件。
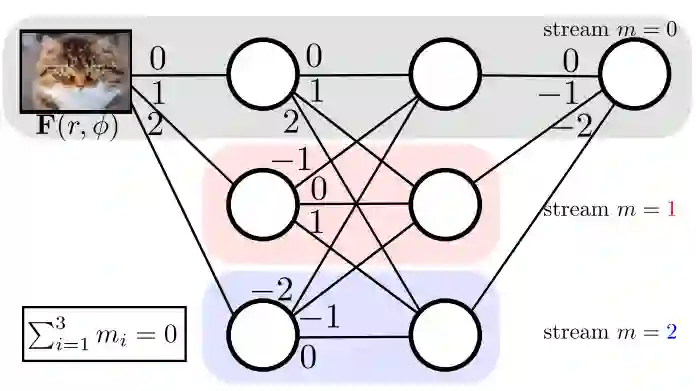
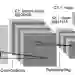
这就是一个有两个隐藏层的H-Net示例,其中输出的m=0。每个横条代表一系列的特征映射,线条表示它们之间的关系,并且表明了对应滤波器的旋转顺序。
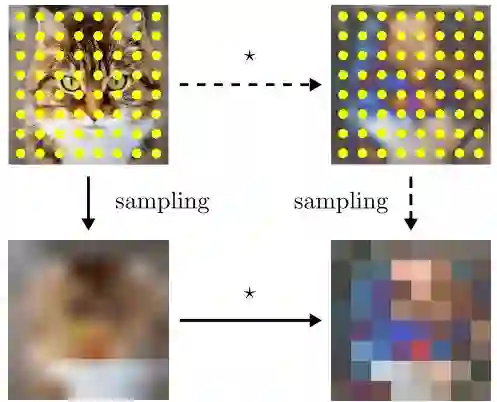
下图是H-Nets在连续的空间域中的采样过程:
实线剪头的流程表示安装过程,虚线表示可能的替代过程,这种方式更容易分析,但是计算起来比较困难。
实验过程
为了评估我们的旋转等变模型,我们在MNIST数据集上进行了基础的分类任务测试,在Berkeley分割数据集上进行了边界检测的测试。我们将我们的标准方法作为当前最新技术的代表,并证明了H-Nets可用于不同架构、不同任务中。
MNITS
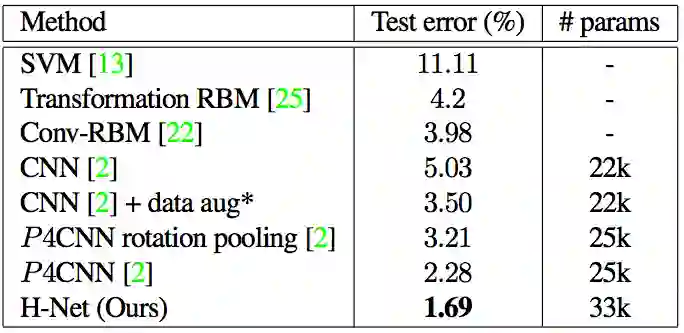
在这一数据集中有10000张训练图片,2000张验证图片和50000张测试图片。将图片进行260°旋转对传统CNN来说是个不小的挑战,但在H-Nets上情况完全不同。以下是实验结果:
可以看到,我们的H-Nets的错误率仅仅为1.69%,是目前最低的。
Berkeley分割数据集
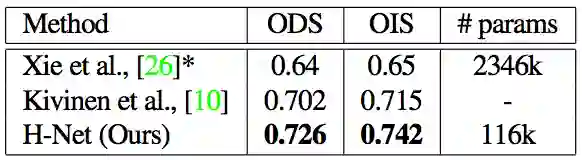
边界检测实际上是非实质性变换,但是边界相对于它的方向是不变的。我们选用了Berkeley的分割数据集(BSD500)来做测试,结果如下:
可以看到我们的方法打败了目前最先进的方法,并且模型均未受过预训练。
结语
UCL本次成果的让H-Nets可以更好地识别旋转360°的图像,精确度得到了大大的提升。研究人员表示,希望未来这一技术可以用在3D应用中,这会让神经网络有更多的可表达性,也会将平移、旋转等对象应用到更大的范围。
原文地址:visual.cs.ucl.ac.uk/pubs/harmonicNets/
GitHub地址:github.com/deworrall92/harmonicConvolutions