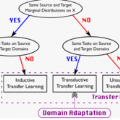
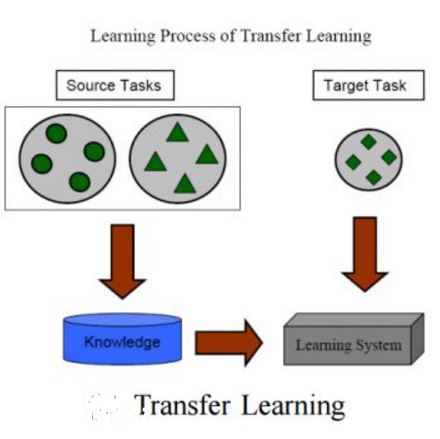
迁移学习:领域自适应的理论分析

极市导读
领域自适应是迁移学习中的重要内容,本文整理了相关的理论文章,与大家分享。>>加入极市CV技术交流群,走在计算机视觉的最前沿
领域自适应即Domain Adaptation,是迁移学习中很重要的一部分内容。目的是把分布不同的源域和目标域的数据,映射到一个特征空间中,使其在该空间中的距离尽可能近。于是在特征空间中对source domain训练的目标函数,就可以迁移到target domain上,提高target domain上的准确率。我最近看了一些理论方面的文章,大致整理了一下,交流分享。
背景
想必大家对GAN都不陌生,GAN是基于对抗的生成网络,主要目标是生成与训练集分布一致的数据。而在迁移学习领域,对抗也是一种常用的方式,如Ganin[1]的论文,使用的网络结构如下图,由三部分组成:特征映射网络 ,标签分类网络 和域判别网络 。
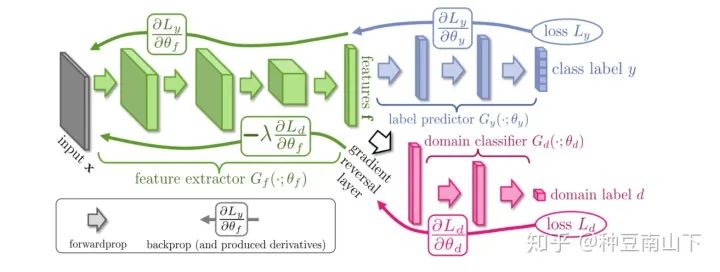
其中,source domain的数据是有标签的,target domain的数据是无标签的。 将source和target domain的数据都映射到一个特征空间 上, 预测标签y, 预测数据来自于target还是source domain。所以流入 的是带标签的source数据,流入 的是不带标签的source和target的数据。
:将数据映射到feature space,使 能分辨出source domain数据的label, 分辨不出数据来自source domain还是target domain。
: 对feature space的source domain数据进行分类,尽可能分出正确的label。
:对feature space的数据进行领域分类,尽量分辨出数据来自于哪一个domain。
最终,希望 与 博弈的结果是source和target domain的数据在feature space上分布已经很一致, 无法区分。于是,可以愉快的用 来分类target domain的数据啦。
理论分析
首先Domain Adaptation基本思想是既然源域和目标域数据分布不一样,那么就把数据都映射到一个特征空间中,在特征空间中找一个度量准则,使得源域和目标域数据的特征分布尽量接近,于是基于源域数据特征训练的判别器,就可以用到目标域数据上。
-
问题建立
假设 是一个实例集(instance set)。
是一个特征空间(feature space)。
是定义在 上的源域数据分布, 是定义在 上的源域特征分布。
、 一样定义目标域数据分布和特征分布。
: 是表示函数(representation function)将实例 映射到 上,即上图的 。
: 是真实的标签函数,是二值函数。我们并不知道 是什么,希望通过训练得到它。
: 是我们自己设计的预测函数,,给定一个特征 ,得到一个其对应的标签,即上图的 。
: 二值函数的集合, 。
接下来需要定义特征到标签的真实映射函数:
注:这边 是随机的是因为,即使 是确定的映射,给定特征 的情况下, 也有可能以不同的概率来自于不同的 。
那么我们自己设计的预测函数 在源域上的错误率:
-
度量准则
接着就需要设计一个度量准则,度量通过 映射到特征空间的特征分布 、 之间的距离。这个距离必须满足的条件是:能通过有限个样本数据计算。
这边找到距离叫 距离,如下:
其中花体 是波莱尔集, 是其一个子集。意思就是取遍所有 的子集,找出在 、 上的概率差的最大值。
给 一个具体的取值,
则此时的 距离可记作 距离:
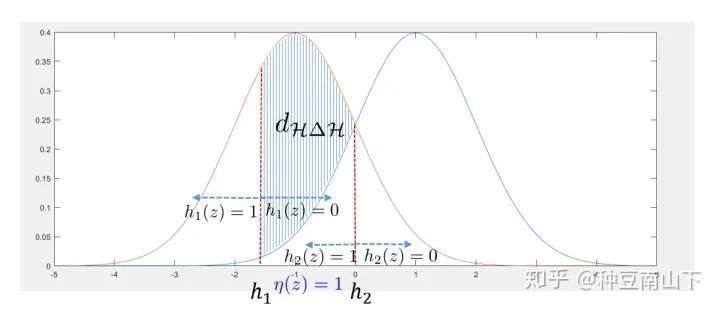
给一个简单的例子,如下:
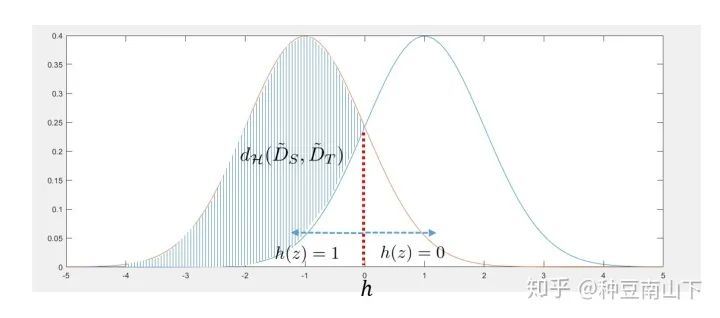
两个高斯分布分别代表源域和目标域的特征分布。由于要取上确界,所以找到的集合 为 。
在 距离的基础上,再定义 距离:
, , XOR operator
简单例子如下:
于是, 可以用下面的界限定:
其中,函数集合
只要取的比 集合
复杂即可,这个很容易达到,我们只需把神经网络设计的复杂一些就行。
从最后的式子来看,如果我们能一个在复杂度足够(能够实现比异或更复杂的操作)的函数类 中,找到一个函数 ,使得 将来自于 的特征 都判为1,将来自于 的特征 都判为0的概率最大,那么我们就能得到 的上界。
其实这边的 就是最开始图中红色的那部分网络 啦!
-
误差界
好了,有了度量准则,那么下面就要介绍最重要的一个定理了。
Theorem: Let R be a fixed representation function from to , is a binary function class, for every :
where,
这个定理说的是,我们训练得到的分类函数 在目标域数据上的错误率,被三个项所限定。第一项是 在源域上的错误率。第二项是通过 将源域、目标域数据都映射到特征空间后,两者特征分布的距离, 即 距离。第三项是一个常数项可以不管。
如果把这些字母都加到开始的图上:
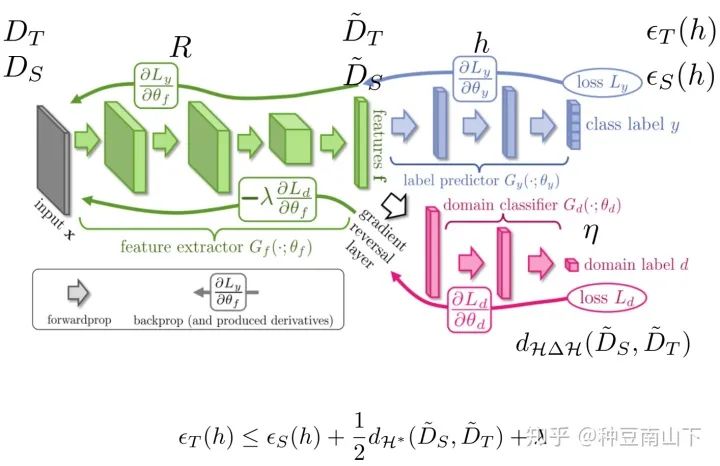
可以看出,要降低 ,表示函数 (即 )承担两项任务,需要降低 在源域上的错误率,还需要减小 距离。而 (即 )承担一项任务目标,就是降低在源域上的错误率。
对于 (即 ),要做的就是尽量能取到 中的上确界,让自己尽量能代表这个距离。其实,我个人想法,这边严格来说并不存在对抗, 并不是一个坏蛋想要增大我们的错误率,它只是在默默的做自己本职的工作,想取到上确界,让自己能代表这个 距离。而 也不是去妨碍 去取上确界,而且想减小上确界本身。
到此,三个网络为什么这么设计应该就很清楚了叭!(至少我觉得讲清楚了233333,当然,最重要的定理的证明我省略了,有兴趣看下面参考的论文。)
-
实际计算
如果引入VC维那一套关于泛化误差的理论,可以得到如下结论:
以 概率成立
是经验损失,可以通过有限数据计算。
是源域数据个数, 是VC维的维数, 是自然底数。
以 概率成立。
可以通过给定数据计算。 表示源域和目标域数据个数。
最终,我们的误差界由下式界定:
-
定理证明
Theorem: Let R be a fixed representation function from to , is a binary function class, for every :
where,
proof:
令 表示特征空间 中被 判为类别1的那些特征的集合。
则有:
这里的 是亦或,也就是 意见不一致的特征组成的集合,即:
所以为什么不等式(1)成立?因为第一项 是 的错误率,包含 意见一致时的判断错误的情况,第二项是意见不一致时的概率,包含 意见不一致时 判断错误的概率。所以 所有判断错误的概率,都包含在后面两项中!
继续往下推:
这一步就没什么好说的了,就是一个数的绝对值大于等于其本身。
不等式(2)的第二项 是在源域上, 意见不一致的概率。一旦意见不一致,那么必然有一方是错的,所以这项必然小于 和 的错误率之和:
根据上文
所以不等式(2)的第三项
所以综合不等式(1-4),有:
定理得证。
参考论文
-
Ben-David, Shai, Blitzer, John, Crammer, Koby, and Pereira, Fernando. Analysis of representations for domain adaptation. In NIPS, pp. 137–144, 2006. -
Ben-David, Shai, Blitzer, John, Crammer, Koby, Kulesza, Alex, Pereira, Fernando, and Vaughan, Jennifer Wort-man. A theory of learning from different domains. JMLR, 79, 2010. -
Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain, Hugo Larochelle, Fran¸cois Laviolette, Mario Marchand, Victor Lempitsky. Domain-Adversarial Training of Neural Networks. Journal of Machine Learning Research 17 (2016) 1-35 -
Ganin, Y., Lempitsky, V.: Unsupervised domain adaptation by backpropagation. arXiv preprint arXiv:1409.7495 (2014)
推荐阅读