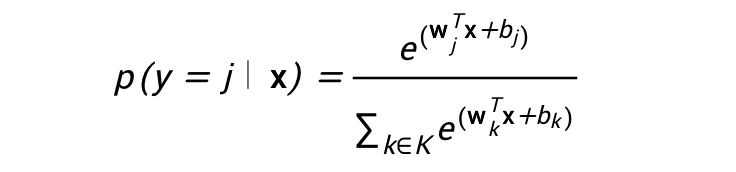神经网络知识专题总结！

 Datawhale干货 

译者：张峰，Datawhale成员

结构总览

一、神经网络简介

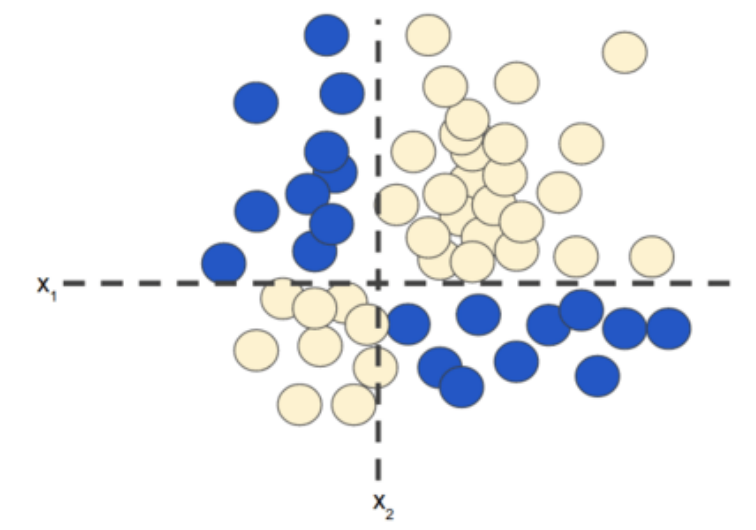
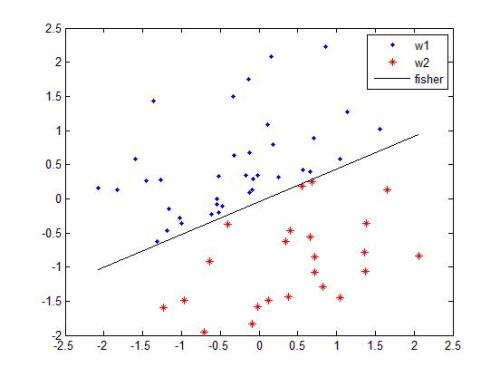
对于非线性分类问题（如图1所示），“非线性”意味着你无法使用形式为：

的模型准确预测标签。也就是说，“决策面”不是直线。之前，我们了解了对非线性问题进行建模的一种可行方法 - 特征组合。

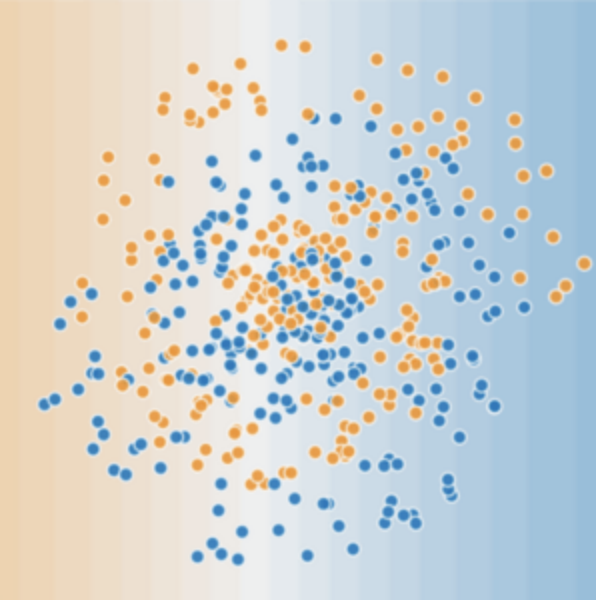
现在，请考虑以下数据集：

图 2. 更难的非线性分类问题

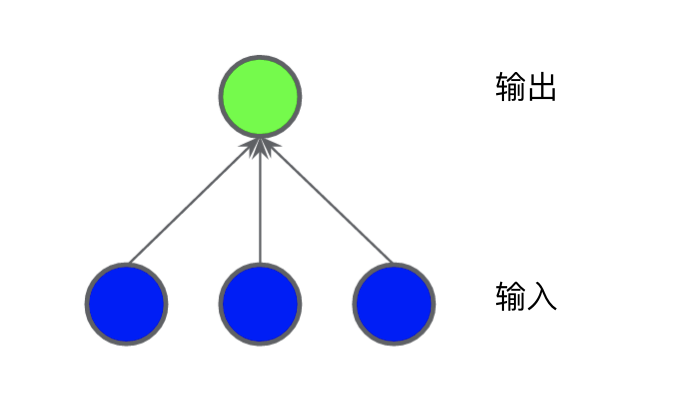
图 2 所示的数据集问题无法用线性模型解决。为了了解神经网络可以如何帮助解决非线性问题，我们首先用图表呈现一个线性模型：

图 3. 用图表呈现的线性模型

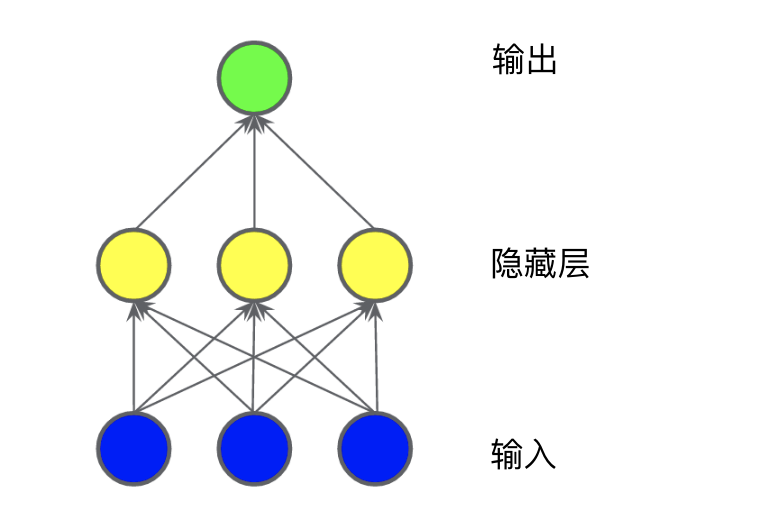
每个蓝色圆圈均表示一个输入特征，绿色圆圈表示各个输入的加权和。要提高此模型处理非线性问题的能力，我们可以如何更改它？

1.1 隐藏层

在下图所示的模型中，我们添加了一个表示中间值的“隐藏层”。隐藏层中的每个黄色节点均是蓝色输入节点值的加权和。输出是黄色节点的加权和。

图 4. 两层模型的图表

此模型是线性的吗？是的，其输出仍是其输入的线性组合。

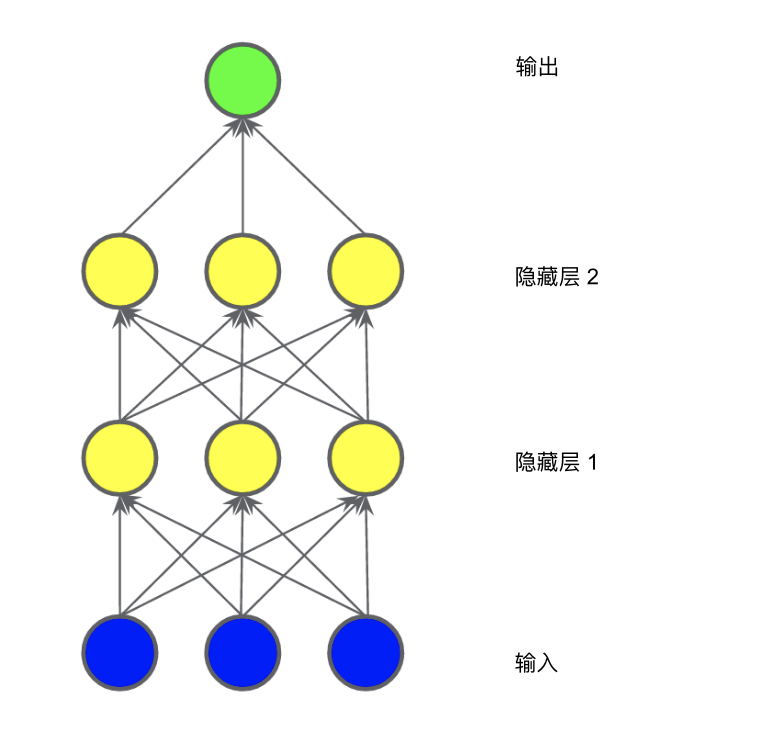
在下图所示的模型中，我们又添加了一个表示加权和的“隐藏层”。

图 5. 三层模型的图表

此模型仍是线性的吗？是的，没错。当你将输出表示为输入的函数并进行简化时，你只是获得输入的另一个加权和而已。该加权和无法对图 2 中的非线性问题进行有效建模。

1.2 激活函数

要对非线性问题进行建模，我们可以直接引入非线性函数。我们可以用非线性函数将每个隐藏层节点像管道一样连接起来。

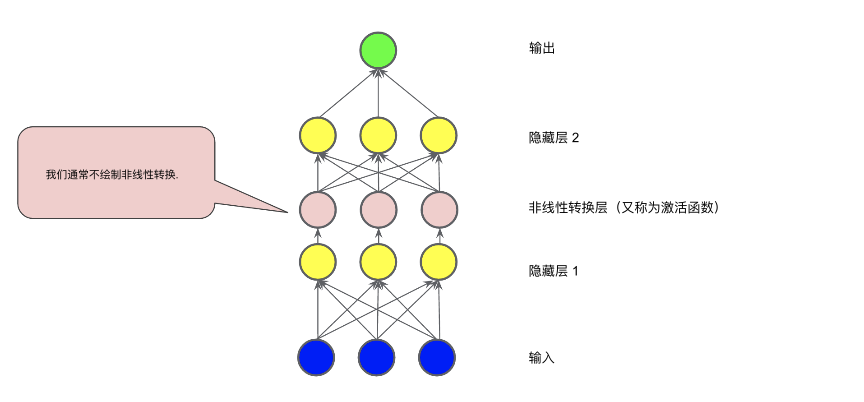
在下图所示的模型中，在隐藏层 1 中的各个节点的值传递到下一层进行加权求和之前，我们采用一个非线性函数对其进行了转换。这种非线性函数称为激活函数。

图 6. 包含激活函数的三层模型的图表

现在，我们已经添加了激活函数，如果添加层，将会产生更多影响。通过在非线性上堆叠非线性，我们能够对输入和预测输出之间极其复杂的关系进行建模。简而言之，每一层均可通过原始输入有效学习更复杂、更高级别的函数。如果你想更直观地了解这一过程的工作原理，请参阅 Chris Olah 的精彩博文。

常见激活函数

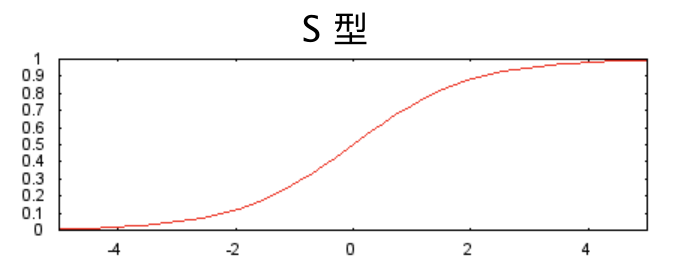
以下 S 型激活函数将加权和转换为介于 0 和 1 之间的值。

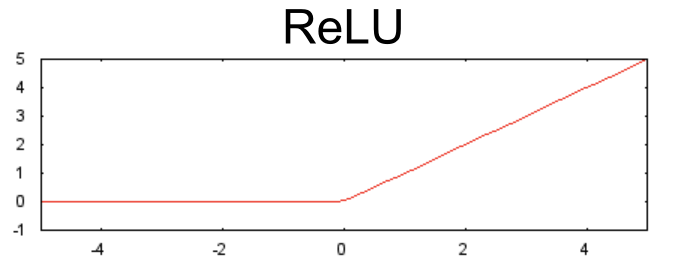
曲线图如下：

图 7. S 型激活函数

相较于 S 型函数等平滑函数，以下修正线性单元激活函数（简称为 ReLU）的效果通常要好一点，同时还非常易于计算。

ReLU 的优势在于它基于实证发现（可能由 ReLU 驱动），拥有更实用的响应范围。S 型函数的响应性在两端相对较快地减少。

图 8. ReLU 激活函数

实际上，所有数学函数均可作为激活函数。假设 σσ 表示我们的激活函数（ReLU、S 型函数等等）。因此，网络中节点的值由以下公式指定：

TensorFlow 为各种激活函数提供开箱即用型支持。但是，我们仍建议从 ReLU 着手。

1.3 小结

现在，我们的模型拥有了人们通常所说的“神经网络”的所有标准组件：

• 一组节点，类似于神经元，位于层中。
• 一组权重，表示每个神经网络层与其下方的层之间的关系。下方的层可能是另一个神经网络层，也可能是其他类型的层。
• 一组偏差，每个节点一个偏差。
• 一个激活函数，对层中每个节点的输出进行转换。不同的层可能拥有不同的激活函数。

警告：神经网络不一定始终比特征组合好，但它确实可以提供适用于很多情形的灵活替代方案。

二、训练神经网络

本部分介绍了反向传播算法的失败案例，以及正则化神经网络的常见方法。

2.1 失败案例

很多常见情况都会导致反向传播算法出错。

梯度消失

较低层（更接近输入）的梯度可能会变得非常小。在深度网络中，计算这些梯度时，可能涉及许多小项的乘积。

当较低层的梯度逐渐消失到 0 时，这些层的训练速度会非常缓慢，甚至不再训练。

ReLU 激活函数有助于防止梯度消失。

梯度爆炸

如果网络中的权重过大，则较低层的梯度会涉及许多大项的乘积。在这种情况下，梯度就会爆炸：梯度过大导致难以收敛。批标准化可以降低学习速率，因而有助于防止梯度爆炸。

ReLU 单元消失

一旦 ReLU 单元的加权和低于 0，ReLU 单元就可能会停滞。它会输出对网络输出没有任何贡献的 0 激活，而梯度在反向传播算法期间将无法再从中流过。由于梯度的来源被切断，ReLU 的输入可能无法作出足够的改变来使加权和恢复到 0 以上。

降低学习速率有助于防止 ReLU 单元消失。

2.2 丢弃正则化

这是称为丢弃的另一种形式的正则化，可用于神经网络。其工作原理是，在梯度下降法的每一步中随机丢弃一些网络单元。丢弃得越多，正则化效果就越强：

• 0.0 = 无丢弃正则化。
• 1.0 = 丢弃所有内容。模型学不到任何规律。

0.0 和 1.0 之间的值更有用。

三、多类别神经网络

3.1 一对多（OnevsAll）

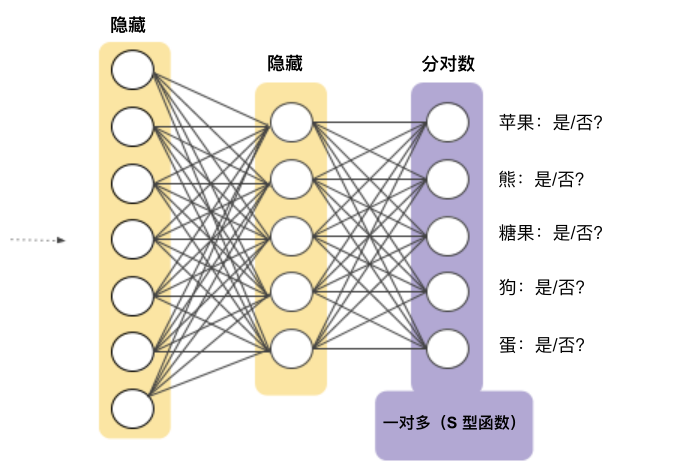
一对多提供了一种利用二元分类的方法。鉴于一个分类问题会有 N 个可行的解决方案，一对多解决方案包括 N 个单独的二元分类器，每个可能的结果对应一个二元分类器。在训练期间，模型会训练一系列二元分类器，使每个分类器都能回答单独的分类问题。以一张狗狗的照片为例，可能需要训练五个不同的识别器，其中四个将图片看作负样本（不是狗狗），一个将图片看作正样本（是狗狗）。即：

1. 这是一张苹果的图片吗？不是。
2. 这是一张熊的图片吗？不是。
3. 这是一张糖果的图片吗？不是。
4. 这是一张狗狗的图片吗？是。
5. 这是一张鸡蛋的图片吗？不是。

当类别总数较少时，这种方法比较合理，但随着类别数量的增加，其效率会变得越来越低下。

我们可以借助深度神经网络（在该网络中，每个输出节点表示一个不同的类别）创建明显更加高效的一对多模型。图9展示了这种方法：

图 9. 一对多神经网络

四、Softmax

我们已经知道，逻辑回归可生成介于 0 和 1.0 之间的小数。例如，某电子邮件分类器的逻辑回归输出值为 0.8，表明电子邮件是垃圾邮件的概率为 80%，不是垃圾邮件的概率为 20%。很明显，一封电子邮件是垃圾邮件或非垃圾邮件的概率之和为 1.0。

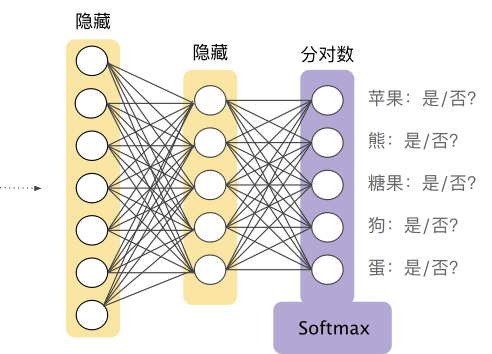
Softmax 将这一想法延伸到多类别领域。也就是说，在多类别问题中，Softmax 会为每个类别分配一个用小数表示的概率。这些用小数表示的概率相加之和必须是 1.0。与其他方式相比，这种附加限制有助于让训练过程更快速地收敛。

例如，回到我们在图 9 中看到的图片分析示例，Softmax 可能会得出图片属于某一特定类别的以下概率：

Softmax 层是紧挨着输出层之前的神经网络层。Softmax 层必须和输出层拥有一样的节点数。

图 10. 神经网络中的 Softmax 层

Softmax 方程式如下所示：

请注意，此公式本质上是将逻辑回归公式延伸到了多类别。

4.1 Softmax 选项

请查看以下 Softmax 变体：

• 完整 Softmax 是我们一直以来讨论的 Softmax；也就是说，Softmax 针对每个可能的类别计算概率。
• 候选采样指 Softmax 针对所有正类别标签计算概率，但仅针对负类别标签的随机样本计算概率。例如，如果我们想要确定某个输入图片是小猎犬还是寻血猎犬图片，则不必针对每个非狗狗样本提供概率。

类别数量较少时，完整 Softmax 代价很小，但随着类别数量的增加，它的代价会变得极其高昂。候选采样可以提高处理具有大量类别的问题的效率。

五、一个标签与多个标签

Softmax 假设每个样本只是一个类别的成员。但是，一些样本可以同时是多个类别的成员。对于此类示例：

• 你不能使用 Softmax。
• 你必须依赖多个逻辑回归。

例如，假设你的样本是只包含一项内容（一块水果）的图片。Softmax 可以确定该内容是梨、橙子、苹果等的概率。如果你的样本是包含各种各样内容（几份不同种类的水果）的图片，你必须改用多个逻辑回归。

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方"AINLP"，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。

阅读至此了，分享、点赞、在看三选一吧🙏