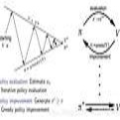
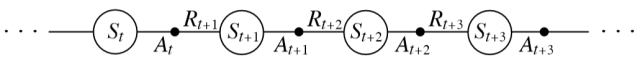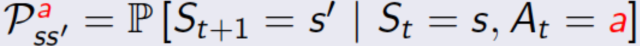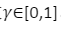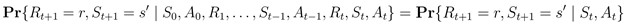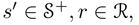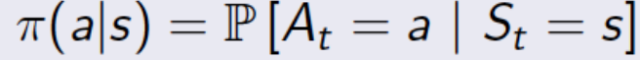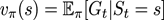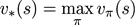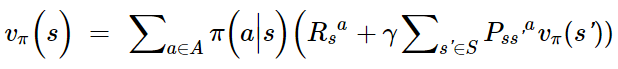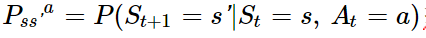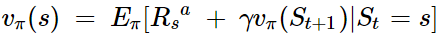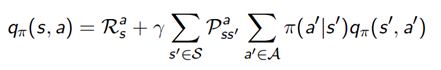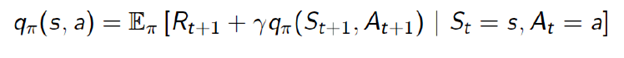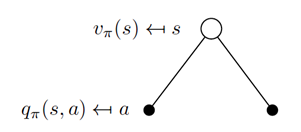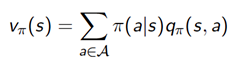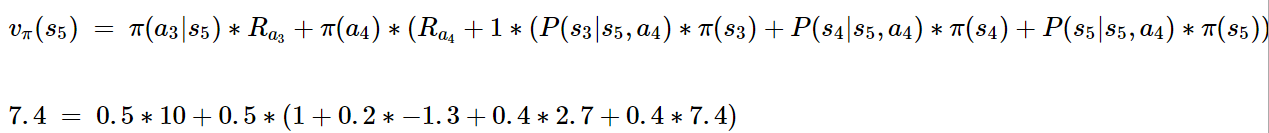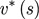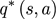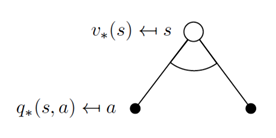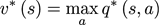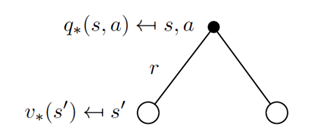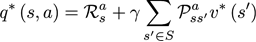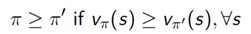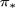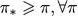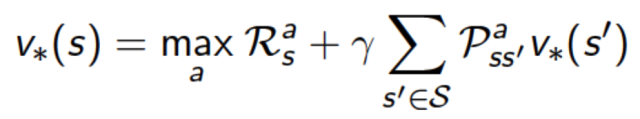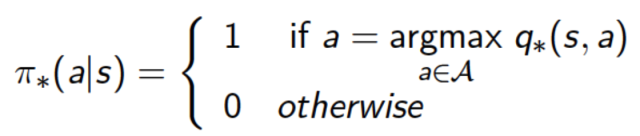马尔科夫决策过程及其性质-CMU深度强化学习第二讲

产业 学术 趣玩

每周推送原创潮流机器人资讯

我们获得授权翻译CMU课程 10703 Deep Reinforcement Learning & Control，这是第二讲。

感谢Katerina Fragkiadaki教授的支持。

翻译贡献者：

刘越江，Segway Robotics  (1-12) 

张浩，蓝胖子机器人Dorabot，(13-21) 

李亚楠，北京理工大学，机器人(22-28) 

罗瑞琨，Umich, Robotics (29-34) 

邱迪聪, CMU, Robotics (35-41) 

Shin, NUS, CS (42-48) 

组长&校对：罗瑞琨

「机器人学家」授权翻译

/********** 刘越江 (1-12)  **********/

马尔科夫

决策过程(MDP)

本讲主要介绍强化学习（Reinforcement Learning，RL）处理的问题模型：马尔科夫决策过程（Markov Decision Processes）。

本讲大纲

• 智能体(Agent)、动作(Action)、奖励(Reward)

• 马尔科夫决策过程(MDP)

• 价值函数(Value function)

• 最优价值函数(Optimal value function)

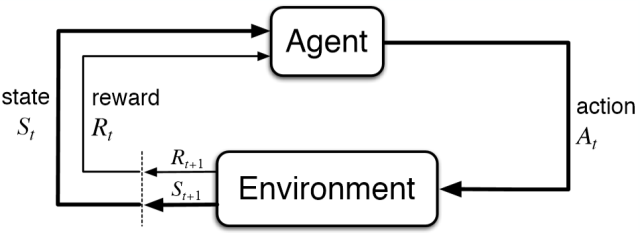
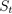
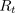
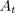
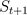
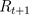
MDP是一个智能体（Agent）与环境（Environment）之间通过动作(Action)、状态(State)和奖励(Reward）相互作用的循环过程。在t时刻，智能体根据从环境中得到的状态和奖励，做出决策动作，在t+1时刻环境反馈给智能体新的状态和奖励 

MDP问题的空间结构 

MDP的时间结构

注意：

• 奖励仅描述了智能体需要实现的目标，而不是如何实现该目标。 

• 在智能体与环境之间设置奖励是一种最简单和廉价的监督形式。 

• 强化学习可以视为开发利用已知策略(exploitation)和探索新策略(exploration)之间的权衡（Sutton 2017)。开发即采用已知的最优策略去得到最好的收益；探索是去尝试未必最优的新策略。

例子：十五子棋

• 状态（state）：棋局的局势（数目大约有1020） 

• 行动（action）：按规则移动棋子。 

• 奖励（reward）：在一局结束后： 

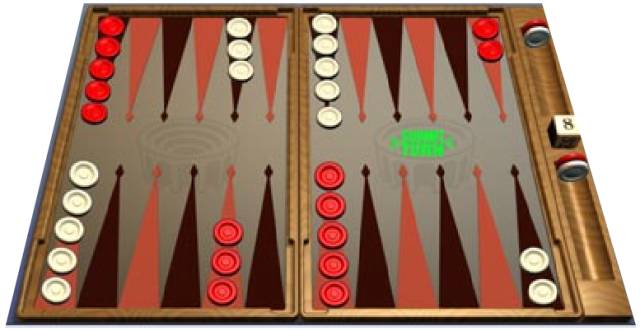
例子：司机的视觉注意力

• 状态（state）：路况、天气、时间 

• 行动（action）：视觉方向（反光镜、摄像头、前方） 

• 奖励（reward）：  

            +1 安全驾驶，非过度疲劳 

            -1 其他驾驶员鸣笛 

• 这个例子中，大量的探索会非常危险，所以需要一个保守的探索策略。这也是很多机器人控制问题的特点。

例子：花样滑冰

滑冰是另一个难以大量探索的例子，需要保守的探索策略

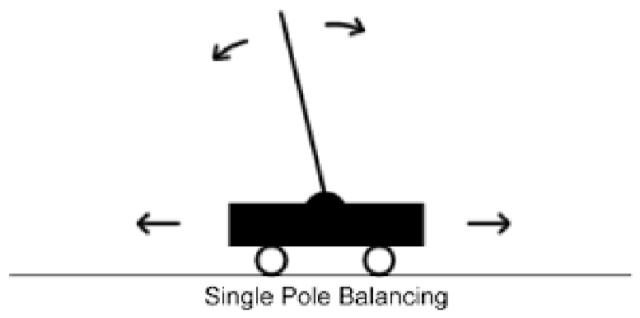
例子：倒立摆问题（低维控制问题）

• 倒立摆问题（Inverted Pendulum,也常叫做cart pole问题，是一个常见的研究基础问题） 

• 状态（state）：杆的角度和角速度 

• 行动（action）：左右移动 

• 奖励（reward）：  

            0 平衡态 

            -1 不平衡

例子：插轴入孔任务（peg in hole）

• 状态（state）：机械臂关节角度状态（7自由度） 

• 行动（action）：关节力矩 

• 奖励（reward）：惩罚抖动的动作（jerky motions），惩罚背离目标姿态的动作 

• peg in hole问题是一类常见的机器人操作的任务。当状态空间（state space）是高维的时候， 只通过奖励来学习是非常困难的。任意的探索会在得到有用的策略前消耗大量的时间。 一些方法，如“构造奖励函数形式（reward shaping）” 通常被用在这样的问题中。比如在LQR问题中使用二阶（quadratic）的代价函数（cost function）。 

MDP

的特征

特征（1） —— 能够检测成功

智能体需要能够明确测量成功的状态。上下图的例子里这个检测都很容易：Peg in hole只需要检测轴是不是已经插到孔中，倒水只需要检查杯子中有没有水。 然而我们经常会遇到不能自动检测任务是否完成的情况。 

特征（2） —— 允许多次尝试、失败

智能体需要有机会尝试（并失败）足够多的次数 。有些问题，因为周期过长，导致不可能有机会尝试足够多的次数。例如“读博士”这样的问题，显然没法为了获取最优策略而读几百遍博士。。 

此外，当安全问题成为顾虑时，试错也变得不可能。例如我们不能通过在真实环境运用强化学习的方法学习自动驾驶，因为交通事故是不被允许的 

/********** 张浩 (13-21)  **********/

MDP

详解 

定义：

• 马尔可夫决策过程（Markov Decision Process， MDP）是一个五元组<S，A，P，R，𝛾> 

• S是状态的有限集合，也叫状态空间 

• A是动作的有限集合，也叫动作空间 

• P是状态转移概率矩阵 

R是奖励函数

γ是折扣系数：

动作

(Actions)

• 目前我们假设动作都是离散的。（之后会讲如何处理连续动作） 

• 对于连续动作，目前我们暂时将其离散化。根据需要，离散化时可以有很多种不同的时间粒度。

状态

(States)

• 状态捕捉了智能体在某一时刻可以获得的所有环境信息。状态可以包括原始的传感器数据，处理过后的传感器数据，以及由一系列数据建立起来的结构化信息，比如记忆等等。 

• 状态应该总结过去的感受，保留足以预测未来的必要的信息。也就是说，状态需要具备马尔可夫性质： 

• 对于所有以及所有历史 

• 当状态已知时，我们就不再需要历史信息了 

• 思考： 

• 扫地机器人的状态应该是什么？

• 自动驾驶汽车的状态信息应该是什么？ 

• 如果一个智能体因为未知的信息而出错，这不能怪罪于智能体；但如果它忽略了能探测到的状态，则不可原谅。（编者注：比如特斯拉自驾车车祸的原因是摄像头无法识别白色背景下的白色卡车，那这个车祸就不是其控制器逻辑的错，而要怪设计系统的人没有让这样一个重要状态变得可观测。但是如果车辆装有激光雷达之类能检测到白色卡车，那控制器逻辑就不可原谅了）

动态模型

(Dynamics)

• 描述一个MDP如何演化。模型描述了智能体在当前的状态和一定动作下，状态会如何变化。 

• 根据是否依赖模型，强化学习的方法可以分为两类： 

• 基于模型的方法：MDP的动态模型必须是已知或者可以估计的。 

• 无模型的方法：策略不依赖于系统的动态模型。 

奖励

(Rewards)

Reward是每次采取action后获得的即时奖励。强化学习的学习目标是最大化未来的奖励之和，通常用“回报（return）”来描述： 

• 定义： 

        回报Gt是从t时刻所能带来的所有打折后奖励的总和 

 

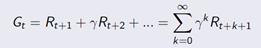
• 强化学习的目标是最大化长期未来奖励，即找到可以最大化Rt+1,Rt+2,Rt+3,...的At 。

• 有些任务中时间范围长度是有限的，比如有终止状态的任务。在这些任务中我们可以使用不打折的奖励。对于无限长度的问题，必须加上小于1的打折系数，才能让Gt是个有限值。 

 

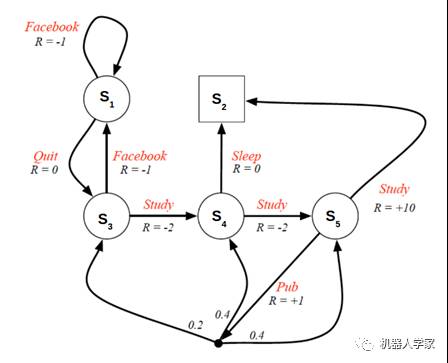
MDP示例：一个学生的生活

以上图学生活动为例。 

• 状态空间S={s1,s2,...,s5}。其中方块表示终止状态，圆圈表示其他状态。 

• 红字表示动作： 

• Facebook 脸书 

• Quit 退出脸书 

• Study 学习 

• Sleep 睡觉 

• Pub (publication)发论文 

• R表示即时奖励 

• 黑色圆点表示如果执行动作a4（发表论文），有0.2的概率下一时刻状态为s3, 0.4的概率为s4, 0.4的概率为s5本身 

策略

（Policy）

定义：智能体学到的策略

π是指已知状态下可能产生动作的概率分布。 

• 策略完整的定义了智能体的行为 

• MDP的策略完全取决于当前状态（而不是历史），也就是说状态是静态的（和当前所处的时刻无关） 

 

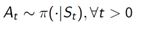
/********** 李亚楠 (22-28)  **********/

MDP

求解

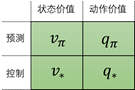
我们的目标找到最优策略，即MDP的最优解。这里把求最优解的过程分为两步： 

1. 预测：给定策略，评估相应的状态价值函数和 状态-动作价值函数 

2. 控制：状态值函数和状态-动作值函数求出后，就可以得到当前状态对应的最优动作 

价值函数

（Value Functions）

• 价值函数用来衡量某一状态或状态-动作对的优劣，即对智能体来说是否值得选择某一状态或在某一状态下执行某一动作。需要注意的是，这里价值函数是依赖于某一策略的。 

• 最优价值函数是在所有策略下的某一状态或状态-动作对的最优值，它不依赖于策略。（译者注：1.为什么会有价值函数这个概念呢？在MDP中我们最终目的是得到一个最优策略π，而策略的优劣取决于长期执行这一策略得到的累计奖励（Reward）。问：怎么算累计奖励？答：价值函数。2.有了价值函数，我们又怎样获取最优策略？单有价值函数还不够，找到了最优的价值函数，自然也就找到了最优策略。 ）

价值函数：累计奖励的期望

定义： 

• 一个MDP的状态价值函数(state-value function) vπ(s)是从状态s出发使用策略π所带来的期望回报。 

  
  

• 动作价值函数(action-value function)qπ(s,a)是从状态s出发，执行动作a后再使用策略π所带来的期望回报。 

  

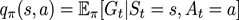
最优价值函数：所有策略下的最优累计奖励期望

最优状态价值函数(optimal state-value function)  v ∗ ( s ) 是所有策略下价值函数的最大值：                                                                             

Bellman

期望方程

• 从公式上看，当前状态的价值和下一步的价值及当前的奖励（Reward）有关。这个公式就是Bellman方程的基本形态，Bellman方程是MDP的基础。 

• 我们可以把上面的状态价值函数分解为当前的奖励和下一步的价值两部分： 

                                                         

• 同样，动作价值函数也能做类似的分解:  

                                         

译者注：此处的即上文所定义的。 

/**********罗瑞琨(29-34)**********/

深入

分析Bellman方程

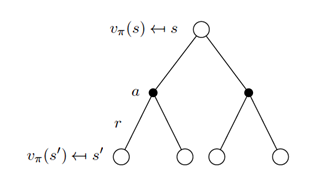
现在我们来看一下Bellman期望方程里的期望的具体形式。下图中，第一层的空心圆圈是当前的状态（state）；向下相连的实心圆圈是在当前状态s下，根据当前的策略，可能采取的动作；第三层的空心圈是采取某一动作后可能的下一时刻的状态s’。 

Bellman期望方程中的期望是在给定某个策略π上的期望，需要注意的是策略π是给定状态s的情况下，动作a的概率分布。所以可以根据上图来计算期望，得到如下的公式：

• 因为动作空间A，状态空间S均为有限集合，所以我们可以用求和来计算期望。公式中的π(a|s)=P(a|s)是状态s下，选择动作a的概率。

• 描述了系统的动态特性， 是在当前时刻，状态为s，动作为a的情况下，下一时刻的状态为s' 的概率。Rsa是状态s下选择动作a的情况下的即时期望奖励。这个公式等价于

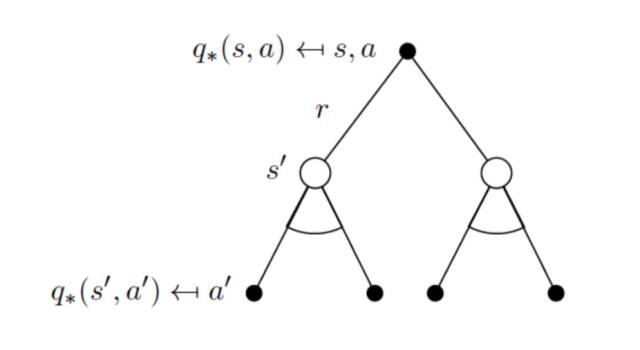
• 相似的，对于动作价值函数我们可以得到下图，第一层的实心圆圈代表当前的状态动作（s，a）；第二层的空心圆圈代表可能的下一时刻的状态s’；第三层的实心圆圈代表下一时刻可能的状态动作（s’，a’）。

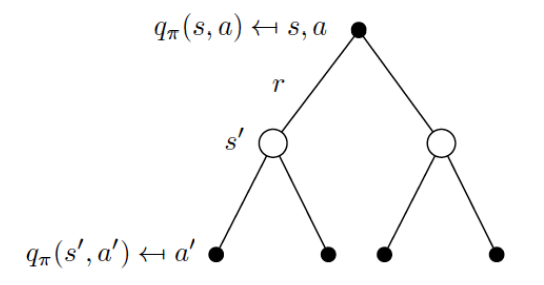
同样的，我们可以得到：

这个公式也等价于： 

状态价值函数和动作价值函数的关系

状态价值函数和动作价值函数的关系可以通过下图来表示。空心圆圈表示当前的状态s，实心圆圈表示当前状态s下可能选择的动作a。 

所以状态价值函数和动作价值函数有如下关系，状态价值函数为动作价值函数在动作a的概率分布下的期望。

相似的，我们可以得到动作价值函数和状态价值函数关系

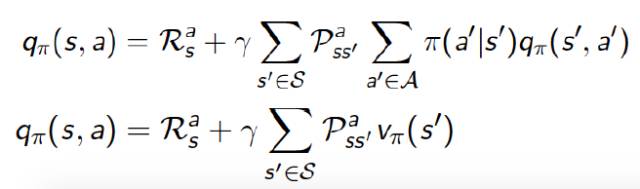
学生活动MDP例子的价值函数

• 以前面提到的学生活动MDP为例，采用均匀随机策略，γ=1。下图中圆圈和方框内的数字代表所在状态的价值。 

• 图中R表示即时奖励。 

• 红色圆圈代表的状态（s5）的价值函数有如下关系： 

/********** 邱迪聪 (35-41) **********/

最优价值函数

Optimal Value Functions

在某个状态（state）下最优价值函数的值，就是智能体（agent）在该状态下，所能获得的累积期望奖励值（cumulative expective rewards）的最大值。 

• 定义： 

• 最优状态－价值函数（optimal state-value function）是在所有策略（policy）中值最大的状态－价值函数，即 

 

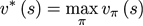
• 最优动作－价值函数（optimal action-value function）是在所有策略中值最大的动作－价值函数，即 

 

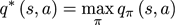
Bellman最优化方程（Bellman Optimality Equations）

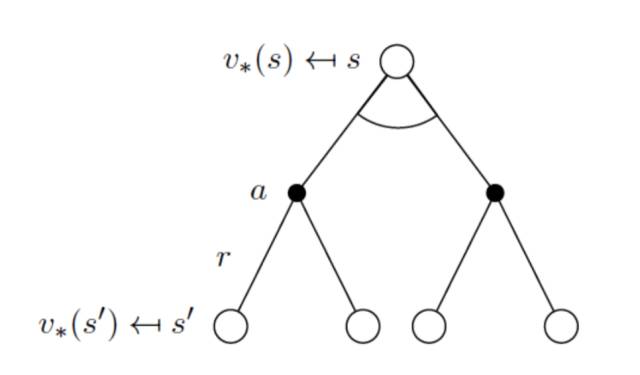
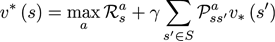
• 最优化原则：一个最优的策略有这样的一种属性，即无论初始状态和初始决策是什么，从某一时刻、某一状态往后看，其后续决策对于从该状态开始的后续问题而言，仍是最优的。（见：Bellamn, 1957, Chap. III.3） 

 

• 动作－价值函数的Bellman方程：

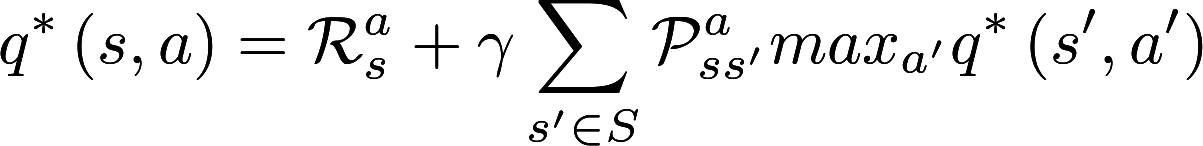
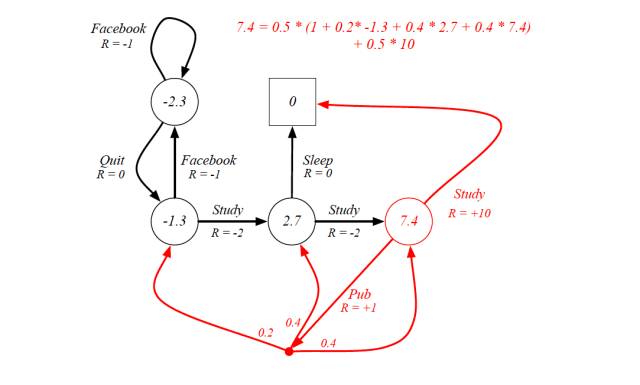
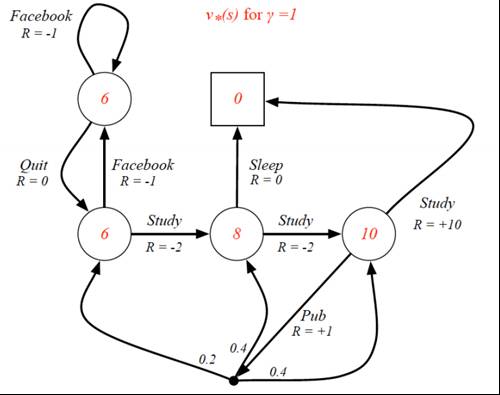
例子：学生活动的最优价值函数

• 以前面提到的学生活动MDP为例，可以得到下面的最优价值函数图 

其中： 

（1） γ=1

（2）R 为即时奖励，可以类比为学生的即时愉悦程度 

（3）红色部分为最优状态－价值函数的值，即学生预计这个状态的长期价值 

 

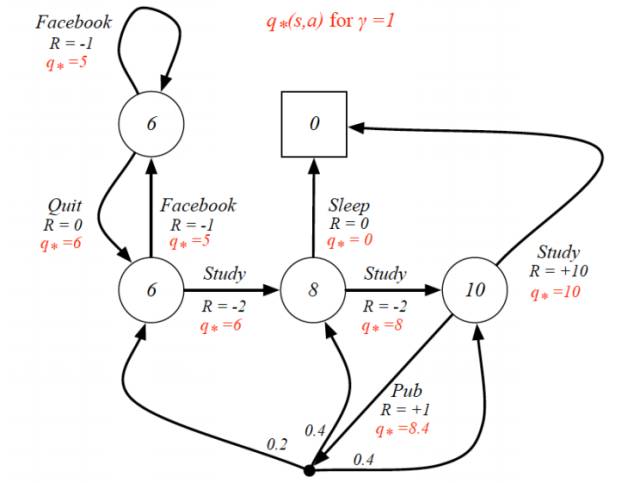
• 同样我们可以得到最优动作价值函数图： 

其中： 

（1） 

（2）R 为即时奖励，可以类比为学生的即时愉悦程度 

（3）红色的 q* 为最优动作－价值函数的值，即学生预计执行这个动作所带来的长期价值 

 

编者（邱迪聪）注：这两个图最重要的地方是，一开始好好学习（Study）获得的即时奖励是负面的，因为学习累呀，哥。可是学着学着却可能带来两个好处，即在最优状态－价值函数的值为 10 的那个时候，因为这两个地方有两个分叉。第一个分叉是 R＝＋10 的那个，这个分叉就是悟出了人生真理，并去睡觉（Sleep）补充精神。领外一个分叉是能够发论文（Pub），然后有一定的概率跳转到三个不同的状态，并且继续愉悦的学习（R > 0）或者不爽的学习（R < 0）。但不要把这个图和实际生活做太大的类比了，F 教授的目的只不过是说即使即时奖励是负面的，可能长期来说这个状态可能是能够带来更大的好处的，所以在 R < 0 的情况下，v* 或者 q* 却有可能是非常好的。（槽点：哪有人发篇论文获得的愉悦程度还不及睡觉呀，而且睡觉就跳进终止是什么一回事嘛，又不是与世长眠，而且怎么可能发完论文还能继续学习不用睡觉嘛。所以说这个只是一个挫例子而已，大家就不要较真了。）

两个最优价值函数的关系

最优状态－价值函数 与 最优动作－价值函数 之间的关系如下： 

1.  可以 用最优动作－价值函数来表达最优状态－价值函数：  

同样，可以用最优状态－价值函数来表达最优动作－价值函数： 

编者（邱迪聪）注：说白了，他们的关系就是一个描述状态的最优价值，另外一个描述在这个状态下执行一个特定动作的最优价值。最优状态－价值函数用来描述处于一个状态的长期最优化价值，即考虑到这个状态下，可能发生的所有后续动作，并且都挑最好的动作来执行的情况下，这个状态的价值。最优动作－价值函数用来描述处于一个状态下并执行某个特定的动作后所带来的长期最优价值，即在这个状态下执行了一个特定的动作，然后考虑到执行这个动作后所有可能处于的后续状态并且在这些状态下总是选取最好的动作来执行所打来的长期价值。

/********** Shin (42-48) **********/

最优策略

（Optimal Policy）

关于收敛性：

• 对策略定义一个偏序： 

定理： 

对于任意Markov决策过程： 

• 存在一个最优策略   , 它比其他任何策略都要好，或者至少都一样好：. 

• 所有最优决策都达到最优值函数， . 

• 所有最优决策都达得最优行动值函数， . 

从最优状态价值函数到最优策略

我们可以从最优状态价值函数 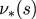 中得到最优策略。  根据Bellman方程，让Max达成的a就是该状态下最优策略的动作。注意，这步计算需要知道系统的动态模型P。 

如果已知最优动作价值函数，最优策略可以通过直接最大化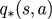来决定：

• 对任何Markov决策过程都有一个确定的最优策略。 

• 我们有了就有了最优策略，不需要动态模型。 

直接求解Bellman最优性方程

理论上直接求解Bellman最优性方程即可获得最优价值函数。但是我们需要考虑如下几方面： 

• 通过解Bellman最优性方程找一个最优策略需要以下条件： 

• 动态模型已知 

• 我们有足够的计算资源和时间 

• 系统满足Markov特性 

• 我们需要多少空间和时间？ 

• 求解方程的计算复杂度是多项式级（感觉还行是不是？） 

• 但是，状态的数量通常会很巨大。（随问题维度指数增加） 

• 所以迭代全空间来精确求解Bellman方程是不可行的。 

• 我们一般会采用近似的方法。 

• D.P.Bertsekas 和 J.N.Tsitsiklis已经借助能够近似Bellman函数的人工神经网络提出了近似动态规划（Dynamic Programming）。 

• 这是一种能够有效减轻维数影响的方法，它采用的是记忆单个神经网络参数而不是去记忆整个空间域完整的函数映射。

近似

强化学习

• 很多RL方法就是在研究如何近似Bellman方程的解。 

• 在未知动态模型中权衡奖励积累和系统认知（模型学习 

• 强化学习是一种在线学习，所以比较容易在那些频繁出现的状态上学到较好的策略（比较接近最优策略），而对于那些较少出现的状态，强化学习往往不能学到很好的策略。这是和传统控制问题的一大区别。（编者注：控制问题里模型已知，对策略的要求往往是在所关心的全部状态空间内都要保证收敛性。）

小结

本节课讨论了：

• Markov决策过程

• 价值函数和最优价值函数

• Bellman方程

• 目前为止我们只讨论了已知动态特性的有限Markov决策过程。

编者注：深度增强学习正处在一个快速发展、迈向应用的时期。它在许多问题上取得了巨大成功，在另一些问题（比如实物的控制问题）上仍面临挑战。不论如何，了解学习这一工具是对机器人专业朋友们很有价值的一件事。

我们的翻译志愿者团队已经超过80人，整个学期的课件每份都已经至少有三人次负责，我们会尽力保证翻译质量。第三四五讲课件已经在翻译中。

CMU 10703 课程网站：请点击阅读原文访问。

英文原版课件下载：请在后台回复“10703”获取下载链接。

本文由微信公众号 机器人学家 编译+整理成文。

转载请联系我们获得许可即可，不尊重作者劳动成果的行为会被举报。

手机长按下图二维码即可关注。