【NeurIPS100】谷歌、Facebook、斯坦福等十篇机器学习最新论文解读

NeurIPS 2019虽然刚刚落幕，但是学习的任务还远未结束。

今天我们整理了NeurIPS 2019上十篇机器学习领域的论文，这些论文来自谷歌、Facebook、普林斯顿大学、斯坦福大学等团队的最新研究成果，供大家参考学习。

1

Differentiable Ranks and Sorting using Optimal Transport

基于优化运输的可微排序

论文作者：

Marco Cuturi, Olivier Teboul, Jean-Philippe Vert（谷歌）

论文地址：

https://www.aminer.cn/pub/5de799899e795e7758069304/

技术领域：

机器学习理论

摘要

排序广泛用于机器学习中，以定义基本算法（例如k最近邻居（k-NN）规则），或定义测试时间指标（例如top-k分类准确性或排名损失）。但是，排序对于深度学习的端到端，可自动区分的管道来说是一种不太好的匹配。排序过程输出两个向量，这两个向量都不是可微的：排序值的向量是分段线性的，而排序置换本身（或它的倒数，即秩的向量）没有可微的性质，因为它是整数值。在本文中，我们提出使用可微分的代理替换常规的排序过程。我们的代理基于这样一个事实，即排序可以看作是一种最佳分配问题，其中要排序的n个值与任何增加的n个目标值族支持的辅助概率测度相匹配。根据此观察，我们通过考虑最佳运输（OT）问题（分配的自然松弛）提出扩展的排序和排序算子，其中辅助度量可以是m个增加值（其中m ≠ n）上支持的任何加权度量。我们通过用熵惩罚对这些OT问题进行正则化来恢复微分算子，并通过应用Sinkhorn迭代来解决它们。使用这些平滑的等级和排序运算符，我们为分类0/1损失以及分位数回归损失提出了可区分的代理。

2

A Simple Baseline for Bayesian Uncertainty in Deep Learning

深度学习中贝叶斯不确定性的简单基准

论文作者：

Wesley Maddox, Timur Garipov, Pavel Izmailov, Dmitry Vetrov, Andrew Gordon Wilson（纽约大学，莫斯科三星人工智能中心，俄罗斯高等经济研究大学）

论文地址：

https://www.aminer.cn/pub/5db92a0a47c8f766461feab6/

技术领域：

机器学习，计算机视觉，模式识别

摘要

本文提出了SWA-Gaussian（SWAG），一种可用于深度学习中不确定性表示和校准的简单、可扩展的通用方法。随机权重平均（SWA）可通过修改后的学习率计划来计算随机梯度下降（SGD）迭代的一阶矩，该方法可改善深度学习的通用性。我们使用SWA解作为一阶矩拟合高斯函数，并且从SGD迭代获得低秩加对角协方差，从而在神经网络权重上形成近似后验分布；然后，再从该高斯分布中采样以执行贝叶斯模型平均。实验结果表明，SWAG近似于真实后验的形状，与SGD迭代的平稳分布的结果一致。此外，与许多流行的替代方案（包括MC-dropout、KFAC Laplace和温度缩放）相比，SWAG在多种计算机视觉任务（包括异常点检测、校准和转移学习）中的性能都很好。

3

AGEM: Solving Linear Inverse Problems via Deep Priors and Sampling

AGEM：通过深度先验和采样解决线性逆问题

论文作者：

Bichuan Guo, Yuxing Han, Jiangtao Wen（清华大学，华南农业大学）

论文地址：

https://www.aminer.cn/pub/5db92a2547c8f766462013e5/

技术领域：

机器学习

摘要

在本文中，我们提出在解决线性逆问题并估计其噪声参数之前，先使用降噪自动编码器（DAE）。现有的基于DAE的方法根据经验估算噪声参数，或将其视为可调超参数。相反，我们建议使用自动编码器指导的EM，这是一种概率性的框架，可以执行具有难解的深层先验的贝叶斯推理。实验证明，可以通过Metropolis-Hastings从DAE获得高效的后验采样，从而可以使用Monte Carlo EM算法。实验结果展示了该方法在信号降噪、图像去模糊和图像去暗角方面的竞争结果。本文的方法是将深度学习的表示能力与贝叶斯统计数据的不确定性量化相结合的示例。

4

Can you trust your model‘s uncertainty？Evaluating predictive uncertainty under dataset shift

可以相信模型的不确定性吗？在数据集偏移下评估预测不确定性

论文作者：

Jasper Snoek, Yaniv Ovadia, Emily Fertig, Balaji Lakshminarayanan, Sebastian Nowozin, D. Sculley, Joshua Dillon, Jie Ren, Zachary Nado（谷歌）

论文地址：

https://www.aminer.cn/pub/5db929c047c8f766461fad18/

技术领域：

机器学习

摘要

深度学习等现代机器学习方法已在监督学习任务的预测准确性上取得了巨大成功，但仍无法对它们的预测不确定性给出有用的估计。量化不确定性在现实环境中尤为关键，由于各种因素（包括样本偏差和不平稳性），不确定性在实际环境中通常涉及输入分布，这些分布由训练分布转换而来。在这种情况下，经过良好校准的不确定性估计可以传达有关何时应该（或不应该）信任模型输出的信息。各种文献中已经提出了许多概率深度学习方法，包括贝叶斯方法和非贝叶斯方法，用于量化预测不确定性。但是据我们所知，过去在数据集转换下没有对这些方法进行严格地大规模实证比较。我们提供了有关分类问题现有的最先进方法的大规模基准，并研究了数据集转化对准确性和校准的影响。我们发现，传统的事后校准以及其他几种方法，效果确实不如新方法效果好。但是，综合多模型的方法在广泛的任务中给出了令人惊讶的强大结果。

5

Implicit Regularization in Deep Matrix Factorization

深度矩阵分解中的隐式正则化

论文作者：

Sanjeev Arora, Nadav Cohen, Wei Hu, Yuping Luo（普林斯顿大学）

论文地址：

https://www.aminer.cn/pub/5d04e910da56295d08de0f0c/

技术领域：

机器学习，神经与演化计算

摘要

努力理解深度学习中的泛化奥秘，导致人们相信基于梯度的优化会带来某种形式的隐式正则化，即对低“复杂度”模型的偏差。我们研究了用于矩阵完成和感知的深度线性神经网络上梯度下降的隐式正则化，该模型称为深度矩阵分解。

在理论和实验的支持下，我们的首个发现是，增加矩阵分解的深度会增强向低秩求解的隐式趋势，通常会导致更准确的恢复。其次，我们提出理论和经验论据，质疑一个新的观点，即可以使用简单的数学范式捕获矩阵分解中的隐式正则化。结果表明，标准正则化的语言可能不够丰富，无法完全包含基于梯度的优化所带来的隐式正则化。

6

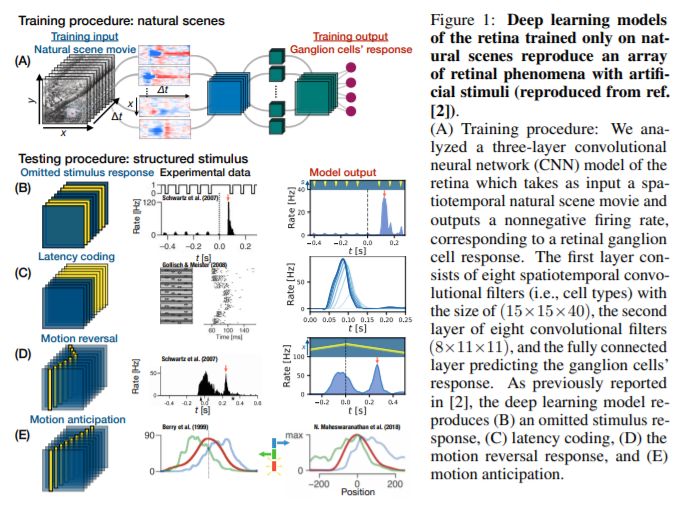
From deep learning to mechanistic understanding in neuroscience: the structure of retinal prediction

从深度学习到神经科学中的机械理解：视网膜预测的结构

论文作者：

Hidenori Tanaka, Aran Nayebi, Niru Maheswaranathan, Lane McIntosh, Stephen Baccus, Surya Ganguli（斯坦福大学）

论文地址：

https://www.aminer.cn/pub/5db92a0447c8f766461fe0dc/

技术领域：

机器学习

摘要

最近，就再现感觉神经元的输入-输出图而言，深度前馈神经网络在对生物感觉过程进行建模方面已经取得了相当大的成功。但是，这种模型对神经科学解释的本质提出了深刻的问题。我们是否只是在不理解的情况下简单地把一个复杂的系统（一个生物回路）替换成另一个系统（一个深层网络）？此外，除了神经表示之外，用于产生神经反应的深度网络的计算机制是否与大脑相同？如果没有一种系统的方法从深度神经网络模型中提取和理解计算机制，那么既难以评估深度学习方法在神经科学中的实用程度，又难以从深度网络中提取出实验可检验的假设。

我们通过将降维与现代归因相结合来开发这种系统的方法，以确定中间神经元对于特定视觉计算的相对重要性。我们将这种方法应用于视网膜的深层网络模型，揭示了对视网膜如何充当预测特征提取器（从不同时空刺激中发出偏离期望值）的概念性理解。对于每种刺激，我们提取的计算机制与先前的科学文献一致，并且在一种情况下产生了新的机制假设。因此，总体而言，这项工作不仅提供了对视网膜惊人预测能力的计算机制的深刻见解，而且还提供了一条新的路线图，超越了比较神经表示的范围，通过提取和理解计算机制，从而将深层网络的框架作为神经科学模型置于更牢固的理论基础上。

7

Practical Deep Learning with Bayesian Principles

贝叶斯原理的深度学习实践

论文作者：

Kazuki Osawa, Siddharth Swaroop, Anirudh Jain, Runa Eschenhagen, Richard E. Turner, Rio Yokota, Mohammad Emtiyaz Khan（东京工业大学，剑桥大学，印度理工学院，卡尔加里大学，瑞肯人工智能项目中心）

论文地址：

https://www.aminer.cn/pub/5db929c047c8f766461fad84/

技术领域：

机器学习

摘要

贝叶斯方法有望解决深度学习的许多缺点，但它们很少与标准方法的性能相匹配，更不用说对其进行改进了。在本文中，我们通过自然梯度变分推断演示了深度网络的实践训练。通过应用批处理归一化、数据增强和分布式训练等技术，即使在大型数据集（例如ImageNet）上，我们也可以在与Adam优化器大致相同的训练周期内获得类似的性能。

重要的是，这种方法保留了贝叶斯原理的优势：很好地校准了预测概率，改善了分布外数据的不确定性，并提高了持续学习的能力。这项工作可以实现实用的深度学习，同时保留贝叶斯原理的优点。其PyTorch实现可作为即插即用优化器使用。

8

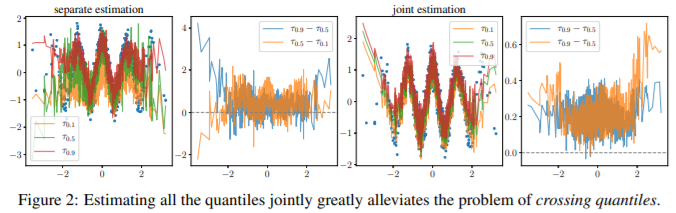
Single-Model Uncertainties for Deep Learning

深度学习的单一模型不确定性

论文作者：

Natasa Tagasovska, David Lopez-Paz（洛桑信息系统部，Facebook）

论文地址：

https://www.aminer.cn/pub/5db92a1247c8f766461ff9b9/

技术领域：

机器学习

摘要

本文为深度神经网络提供了随机不确定性和认知不确定性的单模型评估。为了评估随机性，我们提出了同步分位数回归（SQR），这是一种损失函数，用于学习给定目标变量的所有条件分位数。这些分位数可用于计算校准良好的预测区间。为了评估认知不确定性，我们提出了正交认证（OCs），这是各种非恒定函数的集合，这些函数将所有训练样本映射为零。这些认证将分布范围外的示例映射到非零值，表示认知上的不确定性。我们的不确定性评估器在计算上具有吸引力，因为它们不需被集合或重新训练深层模型即可实现竞争优势。

9

On Exact Computation with an Infinitely Wide Neural Net

关于无限宽神经网络的精确计算

论文作者：

Sanjeev Arora, Simon S. Du, Wei Hu, Zhiyuan Li, Ruslan Salakhutdinov, Ruosong Wang（普林斯顿大学，卡内基梅隆大学）

论文地址：

https://www.aminer.cn/pub/5ce3adb8ced107d4c65bf22a/

技术领域：

机器学习，计算机视觉及模式识别，神经及演化计算

摘要

当经典的深度网络结构（比如AlexNet或者VGG19）的宽度（即卷积层中的通道数和完全连接的内部层中的节点数）允许增无穷大时，它们在标准数据集（如CIFAR-10）上的分类效果如何？在理论上理解深度学习及其关于优化和泛化的奥秘方面，这些问题已成为最重要的问题。它们还将深度学习与高斯过程和核等概念联系起来。最近的一篇论文[Jacot 等，2018]引入了神经正切核（NTK），它捕获了由梯度下降训练的无限宽度中的全连接深度网络的行为；该对象在其他一些最近的论文中也有暗示。这些想法的吸引力在于，使用纯粹基于内核的方法来捕获经过充分训练的无限宽度的深度网络的功能。

本文提供了第一个高效的精确算法，用于计算NTK到卷积神经网络的扩展，我们称之为卷积NTK（CNTK），以及该算法的高效GPU实现。这为在CIFAR-10上纯粹基于内核方法的性能提供了重要的新基准，比[Novak等人2019]中报道的方法高出10％，仅比对应的有限深度网络结构（不用批归一化等）的性能低6％。从理论上讲，我们还给出了第一个非渐近证明，表明经过充分训练的足够宽的网络确实等同于使用NTK的核回归预测器。

参考文献：

Arthur Jacot, Franck Gabriel, and Clément Hongler. Neural tangent kernel: Convergence and generalization in neural networks. arXiv preprint arXiv:1806.07572, 2018.

10

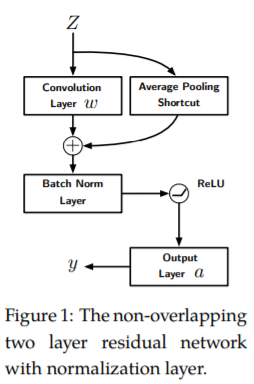
Towards Understanding the Importance of Shortcut Connections in Residual Networks

理解残差网络中快捷连接的重要性

论文作者：

Tianyi Liu, Minshuo Chen, Mo Zhou, Simon S. Du, Enlu Zhou, Tuo Zhao（佐治亚理工学院，杜克大学，北京大学，卡内基梅隆大学）

论文地址：

https://www.aminer.cn/pub/5db9298447c8f766461f893a/

技术领域：

机器学习，优化及控制

摘要

残差网络（ResNet）无疑是深度学习的一个里程碑。ResNet在层之间配备了快捷连接，并使用简单的一阶算法展示了高效的训练。尽管它取得了巨大的成功，但背后的原因远未得到很好的理解。在本文中，我们研究了两层不重叠的卷积ResNet。训练这样的网络需要解决带有虚假的局部最优的非凸优化问题。然而，我们表明，当第一层的权重初始化为0时，并且第二层的权重在一个球面上任意初始化时，梯度下降与适当的归一化相结合，可以避免被虚假局部最优所困，并在多项式时间内收敛到全局最优。数值实验为我们的理论提供了支持。

译者| 赵璇

排版| 学术菠菜

校对| 忆书、青青子衿

责编| 学术青、优学术

NeurIPS100计划是AMiner新推出的一个针对顶会人才和顶会论文的平台化的智能挖掘服务，其目的是对每个顶级会议的100位作者和讲者（人才）进行深度洞察，分析作者之间的关联关系，形成的研究派系、作者的成长路径以及未来的成长脉络预测、跳槽指数等；另外，我们还将针对会议高影响力的100篇重要论文进行深入解读。

往期精彩回顾

【NeurIPS100】NeurIPS2019 七篇获奖论文揭晓 入选论文深度分析！

NeurIPS十年高引学者TOP100榜单发布！这些大牛值得膜拜！

【NeuIPS 2019】Yoshua Bengio报告：如何用深度学习来实现System2？

点击“阅读原文”查看NeurIPS 2019报道及论文解读集合↓