关于不确定性原理，海森堡错了吗？| Science Advances

海森堡不确定性原理曾经面临争议。在一篇新发表于《科学进展》（Science Advances）的论文中，中国科学技术大学几位学者肖芽、许金时、李传峰以及郭光灿，与澳大利亚学者 Wiseman、瑞典学者 Kedem 一起，通过重建单光子在双缝实验中的轨迹，得到了动量传递的分布，再次证明了该理论是正确的。

本文转载自公众号“原理”

撰文 二宗主

1

在量子力学中，“不确定性”是一个高频出现的词汇。有观点认为，不确定性的意思是这个世界具有某种我们无法确定的东西。但多数物理学家认为，不确定性是自然本身的一种固有性质。

固有的不确定性是现代量子力学的创始人之一海森堡的一个核心思想。他提出的不确定性原理表明，我们不可能同时知道一个粒子的所有性质。例如，测量粒子的位置能让我们得知它的位置，但这种测量必然会干扰它的速度，且干扰的程度与位置测量的精度成反比。

海森堡利用不确定性原理解释了测量会如何破坏量子力学的经典特征，我们熟知的双缝干涉就是一个例子。

2

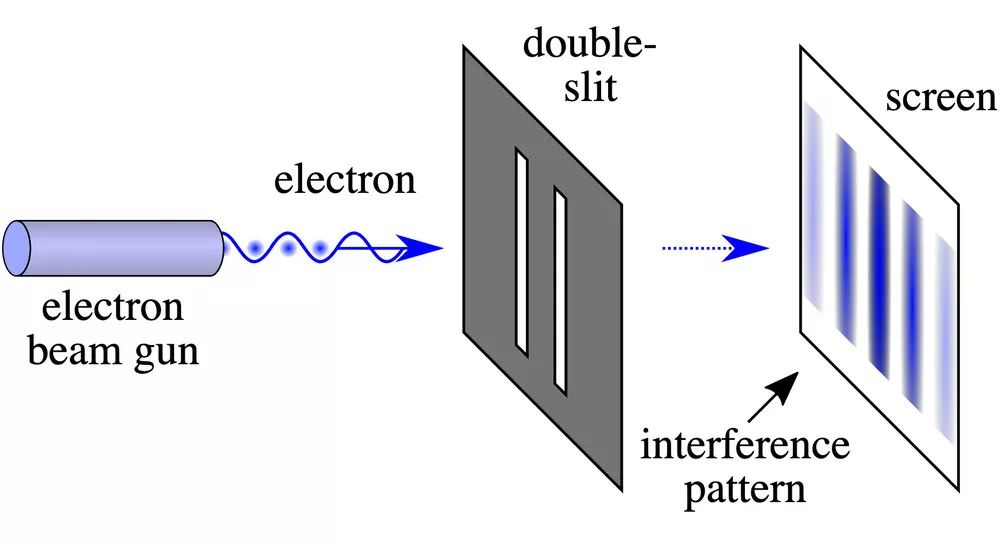
在量子力学里，双缝实验是一种演示量子粒子（如光子、电子等）的波粒二象性的典型实验。实验的设置中会有一个带有两个狭缝的屏障，量子粒子被发射到屏障上，穿过狭缝，在距离屏障的远处所放置的屏幕上生成干涉图样。我们不知道粒子通过的是哪一个狭缝，它的行为就好像它同时通过了两个狭缝，所以形成了干涉图样。

粒子同时通过两个狭缝，在远场的屏幕上形成干涉图样。| 图片来源：Wikimedia

但是如果我们在屏障附近放置一个可以进行位置测量的装置，用以识别粒子穿过的是这两个狭缝中的哪一个，那么我们还能看到干涉图样吗？

我们知道答案是否定的，一旦我们得知粒子穿过的是哪个缝隙（粒子属性），那么屏幕上的干涉图样（波属性）就会被破坏。海森堡的解释是，如果我们能通过位置测量来足够清楚地了解粒子是从哪个缝隙穿过的，就会给速度带来一个随机的干扰。我们对它穿过哪个缝隙的信息掌握得越清楚，干涉条纹的可见度就会越低。

然而长期以来，关于这种位置测量是否是通过干扰粒子的动量（速度）而使得干涉图样消失的，一直是物理学家争论的问题。量子物理学家认为，我们并不需要进行这样的位置测量来找出粒子穿过的是哪个狭缝。对任何依赖于粒子穿过了哪个狭缝才能给出测量结果的测量，都可以做到这一点。因此，有量子物理学家认为，能解释干涉图样消失的不是海森堡的不确定性原理，而是某些其他的机制。

3

早在上世纪 90 年代初，就有量子物理学家对这个问题进行过实验论证。1991 年，Scully、Englert 和 Walther（SEW）几位物理学家证明，他们可以在不明显干扰粒子动量的情况下，以相当精确的位置测量来识别一个粒子通过了双缝实验中的哪一个狭缝。难道海森堡错了吗？

到了 1994 年，Storey、Tan、Collett、和 Walls（STCW）提出了一种一般形式，得到了与 SEW 相反的结论。STCW 表明，探测到粒子穿过的是哪个狭缝这一信息，必然会涉及到粒子的一些动量传递。

随后，物理学家 Wiseman 和 Harrison 通过仔细分析后解决了这个矛盾，在一篇发表于 1995 年的论文中，他们指出 SEW 和 STCW 分别使用了不同的动量传递概念——一个是“经典”的，一个是“量子”的，也就是说，这两种结论实际上是互补的。

在一篇新发表于《科学进展》的论文中，中国科学技术大学几位学者肖芽、许金时、李传峰以及郭光灿，与 Wiseman 和 Kedem 一起，通过重建单光子在双缝实验中的轨迹，得到了动量传递的分布。简单来说，他们从两个狭缝中的许多不同起点来重建光子的运动，然后比较没有测量装置和有测量装置情况下速度随时间的变化，从而确定了由测量引起的速度变化。

他们发现，速度的变化不是在测量光子通过了哪个缝隙时出现的，而是被推迟到粒子穿过狭缝之后，在通往屏幕的传播过程中出现了累积的速度变化。这是为什么？答案是，因为光子不仅仅是粒子，它们也是波。他们进一步地确认了干涉图样的消失与后期的总动量干扰之间的关系，确定了粒子的速度所受到的干扰大小与海森堡的不确定性原理预测的一致。

实验表明，测量对粒子速度的影响会在粒子离开测量装置之后的很长一段时间内持续，最远可达 5 米。在远处的时候，累积的速度变化就已经足够大，足以破坏掉干涉图样中的波纹。

如此来看，海森堡的不确定性原理取得了胜利。

参考链接：

[1] https://advances.sciencemag.org/content/5/6/eaav9547 

[2] https://theconversation.com/quantum-physics-experiment-shows-heisenberg-was-right-about-uncertainty-in-a-certain-sense-118456

论文信息

【标题】Observing momentum disturbance in double-slit “which-way” measurements

【作者】Ya Xiao, Howard M. Wiseman, Jin-Shi Xu, Yaron Kedem, Chuan-Feng Li, and Guang-Can Guo

【期刊】Science Advances

【时间】14 Jun 2019

【DOI】10.1126/sciadv.aav9547

【链接】https://advances.sciencemag.org/content/5/6/eaav9547

【摘要】Making a “which-way” measurement (WWM) to identify which slit a particle goes through in a double-slit apparatus will reduce the visibility of interference fringes. There has been a long-standing controversy over whether this can be attributed to an uncontrollable momentum transfer. Here, by reconstructing the Bohmian trajectories of single photons, we experimentally obtain the distribution of momentum change. For our WWM, the change we see is not a momentum kick that occurs at the point of the WWM, but rather one that nonclassically accumulates during the propagation of the photons. We further confirm a quantitative relation between the loss of visibility consequent on a WWM and the total (late-time) momentum disturbance. Our results emphasize the role of the Bohmian momentum in giving an intuitive picture of wave-particle duality and complementarity.

本文转载自公众号“原理”（ID: principia1687）

---

▽ 精彩回顾 ▽