Python 机器学习算法实践:树回归
(点击上方蓝字,快速关注我们)
来源:伯乐在线 - iPytLab
前言
最近由于开始要把精力集中在课题的应用上面了,这篇总结之后算法原理的学习先告一段落。本文主要介绍决策树用于回归问题的相关算法实现,其中包括回归树(regression tree)和模型树(model tree)的实现,并介绍了预剪枝(preprune)和后剪枝(postprune)的防止树过拟合的技术以及实现。最后对回归树和标准线性回归进行了对比。
正文
在之前的文章中我总结了通过使用构建决策树来进行类型预测。直观来看树结构最容易对分类问题进行处理,通过递归我们在数据中选取最佳分割特征对训练数据进行分割并进行树分裂最终到达触底条件获得训练出来决策树,可以通过可视化的方式直观的查看训练模型并对数据进行分类。
通常决策树树分裂选择特征的方法有ID3, C4.5算法, C5.0算法和CART树。在《机器学习算法实践-决策树(Decision Tree)》中对ID3以及C4.5算法进行了介绍并使用ID3算法处理了分类问题。本文主要使用决策树解决回归问题,使用CART(Classification And Regression Trees)算法。
CART
CART是一种二分递归分割的技术,分割方法采用基于最小距离的基尼指数估计函数,将当前的样本集分为两个子样本集,使得生成的的每个非叶子节点都有两个分支。因此,CART算法生成的决策树是结构简洁的二叉树。
分类树是针对目标变量是离散型变量,通过二叉树将数据进行分割成离散类的方法。而回归树则是针对目标变量是连续性的变量,通过选取最优分割特征的某个值,然后数据根据大于或者小于这个值进行划分进行树分裂最终生成回归树。
特征和最佳分割点的选取
在使用决策树解决回归问题中我们需要不断的选取某一特征的一个值作为分割点来生成子树。选取的标准就是使得被分割的两部分数据能有最好的纯度。
对于离散型数据我们可以通过计算分割两部分数据的基尼不纯度的变化来判定最有分割点;
对于连续性变量我们通过计算最小平方残差,也就是选择使得分割后数据方差变得最小的特征和分割点。直观的理解就是使得分割的两部分数据能够有最相近的值。
树分裂的终止条件
有了选取分割特征和最佳分割点的方法,树便可以依此进行分裂,但是分裂的终止条件是什么呢?
节点中所有目标变量的值相同, 既然都已经是相同的值了自然没有必要在分裂了,直接返回这个值就好了.
树的深度达到了预先指定的最大值
不纯度的减小量小于预先定好的阈值,也就是之进一步的分割数据并不能更好的降低数据的不纯度的时候就可以停止树分裂了。
节点的数据量小于预先定好的阈值
回归树的Python实现
本部分使用Python实现简单的回归树,并对给定的数据进行回归并可视化回归曲线和树结构。完整代码详见: https://github.com/PytLab/MLBox/tree/master/classification_and_regression_trees
首先是加载数据的部分,这里的所有测试数据我均使用的《Machine Learning in Action》中的数据,格式比较规整加载方式也比较一致, 这里由于做树回归,自变量和因变量都放在同一个二维数组中:
def load_data(filename):
''' 加载文本文件中的数据.
'''
dataset = []
with open(filename, 'r') as f:
for line in f:
line_data = [float(data) for data in line.split()]
dataset.append(line_data)
return dataset
树回归中再找到分割特征和分割值之后需要将数据进行划分以便构建子树或者叶子节点:
def split_dataset(dataset, feat_idx, value):
''' 根据给定的特征编号和特征值对数据集进行分割
'''
ldata, rdata = [], []
for data in dataset:
if data[feat_idx] < value:
ldata.append(data)
else:
rdata.append(data)
return ldata, rdata
然后就是重要的选取最佳分割特征和分割值了,这里我们通过找到使得分割后的方差最小的分割点最为最佳分割点:
def choose_best_feature(dataset, fleaf, ferr, opt):
''' 选取最佳分割特征和特征值
dataset: 待划分的数据集
fleaf: 创建叶子节点的函数
ferr: 计算数据误差的函数
opt: 回归树参数.
err_tolerance: 最小误差下降值;
n_tolerance: 数据切分最小样本数
'''
dataset = np.array(dataset)
m, n = dataset.shape
err_tolerance, n_tolerance = opt['err_tolerance'], opt['n_tolerance']
err = ferr(dataset)
best_feat_idx, best_feat_val, best_err = 0, 0, float('inf')
# 遍历所有特征
for feat_idx in range(n-1):
values = dataset[:, feat_idx]
# 遍历所有特征值
for val in values:
# 按照当前特征和特征值分割数据
ldata, rdata = split_dataset(dataset.tolist(), feat_idx, val)
if len(ldata) < n_tolerance or len(rdata) < n_tolerance:
# 如果切分的样本量太小
continue
# 计算误差
new_err = ferr(ldata) + ferr(rdata)
if new_err < best_err:
best_feat_idx = feat_idx
best_feat_val = val
best_err = new_err
# 如果误差变化并不大归为一类
if abs(err - best_err) < err_tolerance:
return None, fleaf(dataset)
# 检查分割样本量是不是太小
ldata, rdata = split_dataset(dataset.tolist(), best_feat_idx, best_feat_val)
if len(ldata) < n_tolerance or len(rdata) < n_tolerance:
return None, fleaf(dataset)
return best_feat_idx, best_feat_val
其中,停止选取的条件有两个: 一个是当分割的子数据集的大小小于一定值;一个是当选取的最佳分割点分割的数据的方差减小量小于一定的值。
fleaf是创建叶子节点的函数引用,不同的树结构此函数也是不同的,例如本部分的回归树,创建叶子节点就是根据分割后的数据集平均值,而对于模型树来说,此函数返回值是根据数据集得到的回归系数。ferr是计算数据集不纯度的函数,不同的树模型该函数也会不同,对于回归树,此函数计算数据集的方差来判定数据集的纯度,而对于模型树来说我们需要计算线性模型拟合程度也就是线性模型的残差平方和。
然后就是最主要的回归树的生成函数了,树结构肯定需要通过递归创建的,选不出新的分割点的时候就触底:
def create_tree(dataset, fleaf, ferr, opt=None):
''' 递归创建树结构
dataset: 待划分的数据集
fleaf: 创建叶子节点的函数
ferr: 计算数据误差的函数
opt: 回归树参数.
err_tolerance: 最小误差下降值;
n_tolerance: 数据切分最小样本数
'''
if opt is None:
opt = {'err_tolerance': 1, 'n_tolerance': 4}
# 选择最优化分特征和特征值
feat_idx, value = choose_best_feature(dataset, fleaf, ferr, opt)
# 触底条件
if feat_idx is None:
return value
# 创建回归树
tree = {'feat_idx': feat_idx, 'feat_val': value}
# 递归创建左子树和右子树
ldata, rdata = split_dataset(dataset, feat_idx, value)
ltree = create_tree(ldata, fleaf, ferr, opt)
rtree = create_tree(rdata, fleaf, ferr, opt)
tree['left'] = ltree
tree['right'] = rtree
return tree
使用回归树对数据进行回归
这里使用了现成的分段数据作为训练数据生成回归树,本文所有使用的数据详见: https://github.com/PytLab/MLBox/tree/master/classification_and_regression_trees
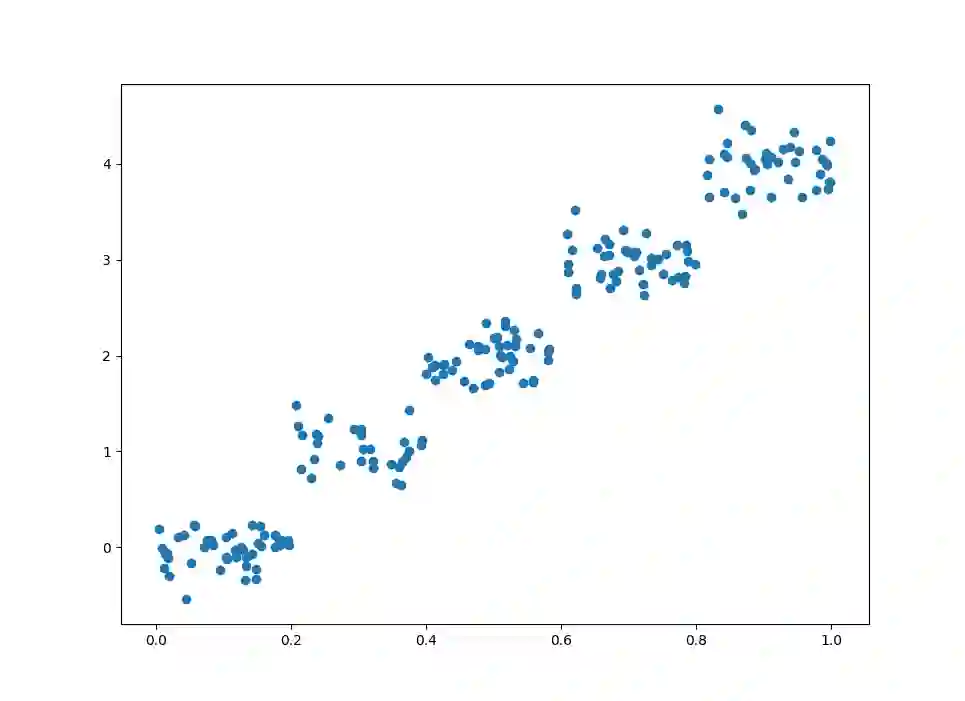
可视化数据点
dataset = load_data('ex0.txt')
dataset = np.array(dataset)
# 绘制散点
plt.scatter(dataset[:, 0], dataset[:, 1])
创建回归树并可视化
看到这种分段的数据,回归树拟合它可是最合适不过了,我们创建回归树:
tree = create_tree(dataset, fleaf, ferr, opt={'n_tolerance': 4,
'err_tolerance': 1})
通过Python字典表示的回归树结构:
{'feat_idx': 0,
'feat_val': 0.40015800000000001,
'left': {'feat_idx': 0,
'feat_val': 0.20819699999999999,
'left': -0.023838155555555553,
'right': 1.0289583666666666},
'right': {'feat_idx': 0,
'feat_val': 0.609483,
'left': 1.980035071428571,
'right': {'feat_idx': 0,
'feat_val': 0.81674199999999997,
'left': 2.9836209534883724,
'right': 3.9871631999999999}}}
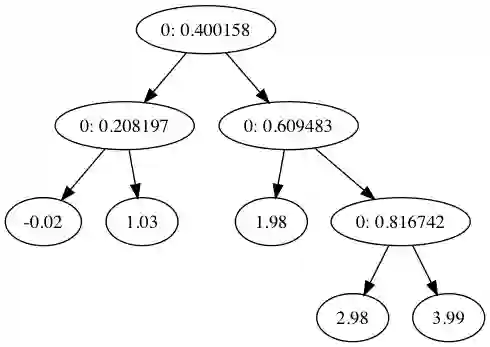
这里我还是使用Graphviz来可视化回归树,类似之前决策树做分类的文章中的dotify函数,这里稍微修改下叶子节点的label,我们便可以递归得到决策树对应的dot文件, dotify函数的实现见:https://github.com/PytLab/MLBox/blob/master/classification_and_regression_trees/regression_tree.py#L159
然后获取树结构图:
datafile = 'ex0.txt'
dotfile = '{}.dot'.format(datafile.split('.')[0])
with open(dotfile, 'w') as f:
content = dotify(tree)
f.write(content)
生成回归树图片:
dot -Tpng ex0.dot -o ex0_tree.png
其中节点上数字代表:特征编号: 特征分割值
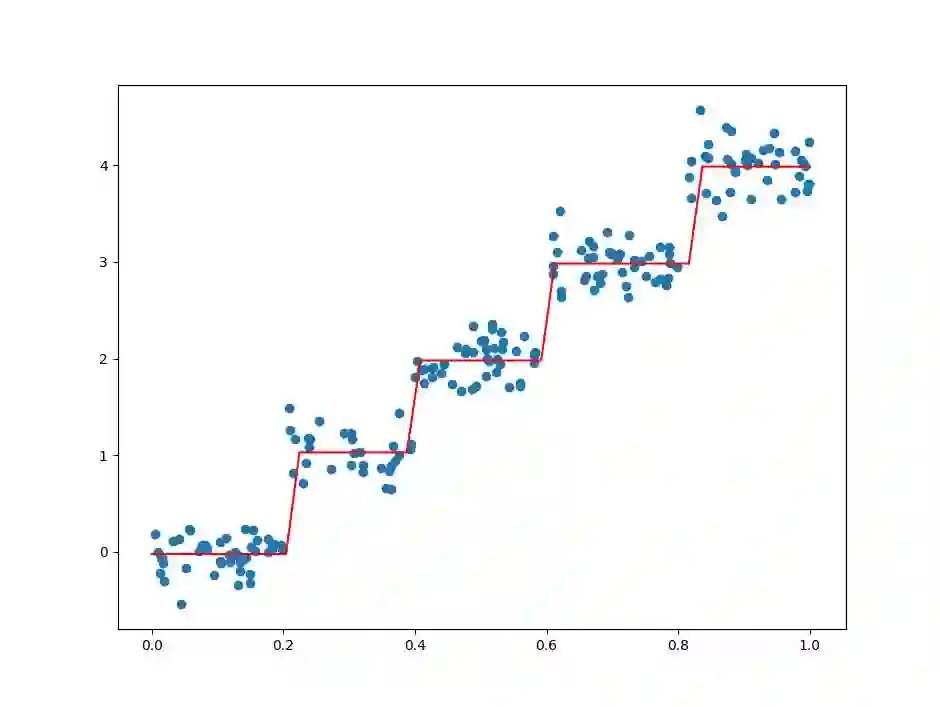
绘制回归树回归曲线
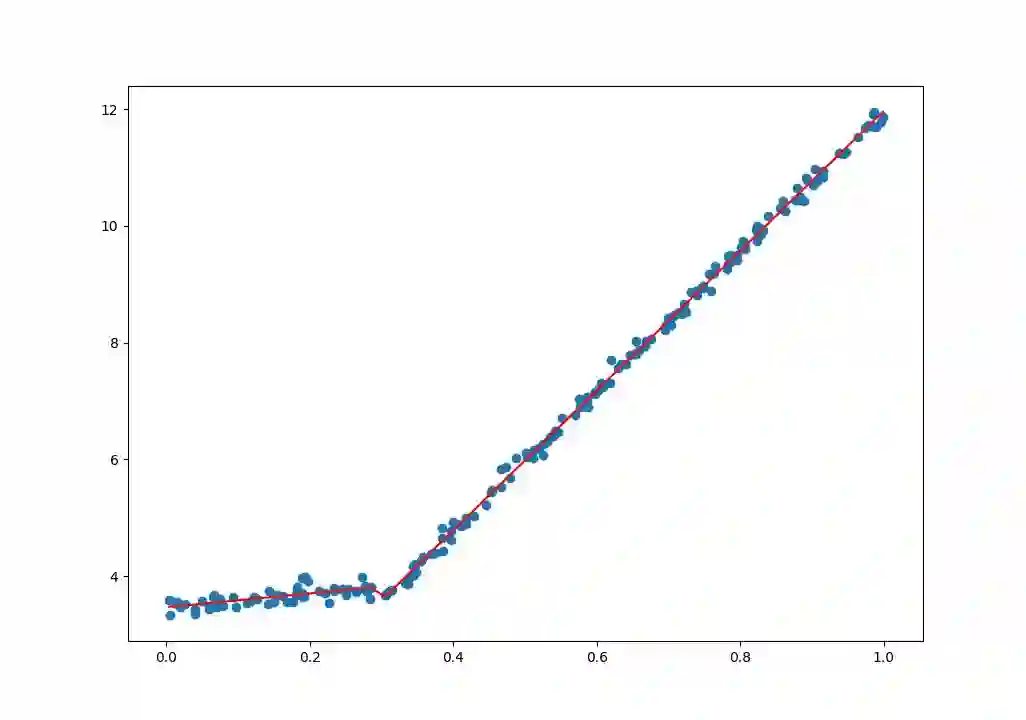
有了回归树,我们便可以绘制回归树回归曲线,看看它对于分段数据是否能有较好的回归效果:
# 绘制回归曲线
x = np.linspace(0, 1, 50)
y = [tree_predict([i], tree) for i in x]
plt.plot(x, y, c='r')
plt.show()
树剪枝
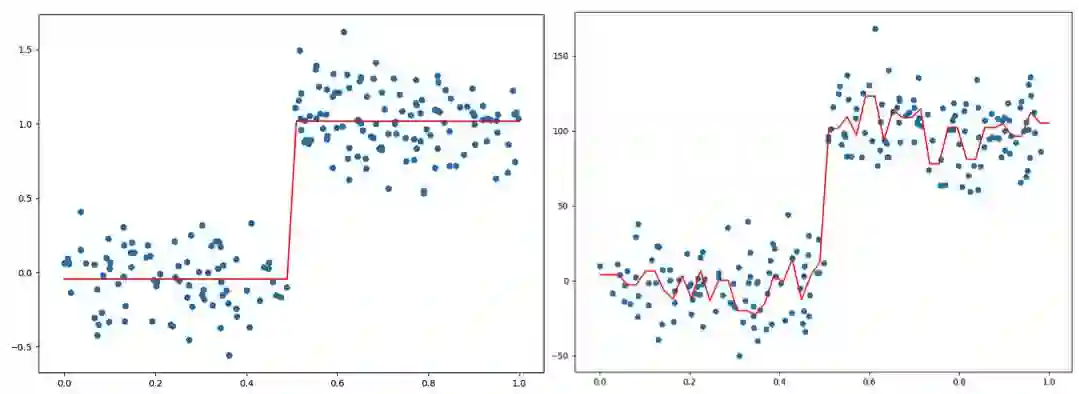
在介绍树剪枝之前先使用上一部分的代码对两组类似的数据进行回归,可视化后的数据以及回归曲线如下(数据文件左&数据文件右):
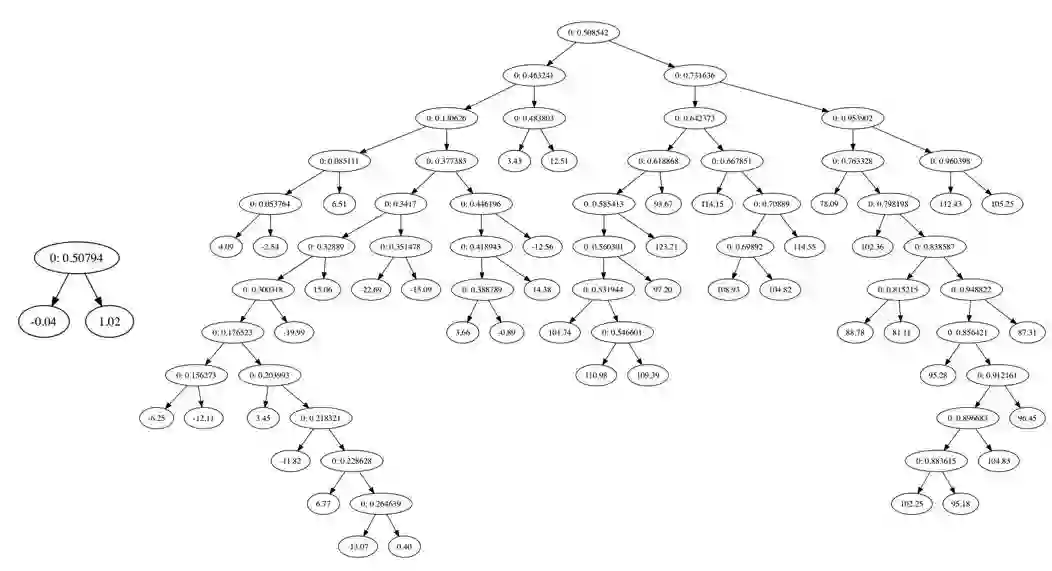
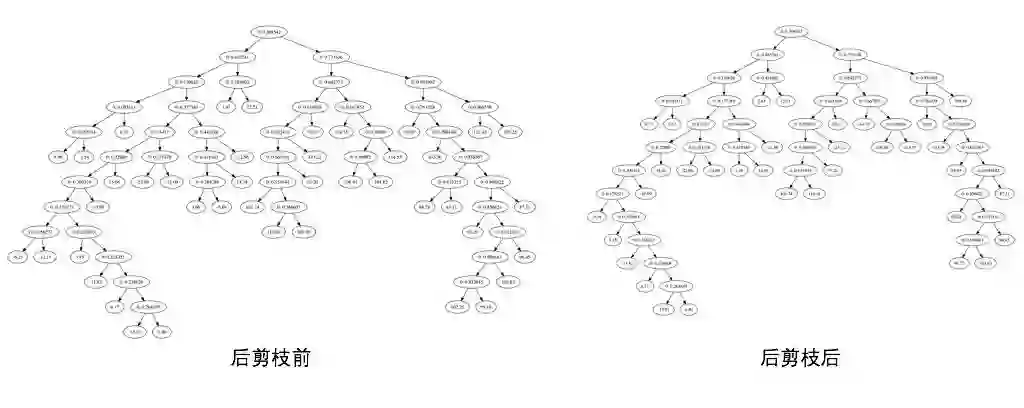
左右两边的数据的分布基本相同但是使用相同的参数得到的回归树却完全不同左边的回归树只有两个分支,而右边的分支则有很多,甚至有时候会为所有的数据点得到一个分支,这样回归树将会非常的庞大, 如下是可视化得到的两个回归树:
如果一棵树的节点过多则表明该模型可能对数据进行了“过拟合”。那么我们需要降低决策树的复杂度来避免过拟合,此过程就是剪枝。剪枝技术又分为预剪枝和后剪枝。
预剪枝
预剪枝是在生成决策树之前通过改变参数然后在树生成的过程中进行的。比如在上文中我们创建回归树的函数中有个opt参数,其中包含n_tolerance和err_tolerance,他们可以控制何时停止树的分裂,当增大叶子节点的最小数据量以及增大误差容忍度,树的分裂也会越提前的终止。当我们把误差变化容忍度增加到2000的时候得到的回归树以及回归曲线可视化如下:
后剪枝
预剪枝技术需要用于预先指定参数,但是后剪枝技术则是通过测试数据来自动进行剪枝不需要用户干预因此是一种更理想的剪枝技术,但是我们需要写剪枝函数来处理。
后剪枝的大致思想就是我们针对一颗子树,尝试将其左右子树(节点)合并,通过测试数据计算合并前后的方差,如果合并后的方差比合并前的小,这说明可以合并此子树。
对树进行塌陷处理: 我们对一棵树进行塌陷处理,就是递归将这棵树进行合并返回这棵树的平均值。
def collapse(tree):
''' 对一棵树进行塌陷处理, 得到给定树结构的平均值
'''
if not_tree(tree):
return tree
ltree, rtree = tree['left'], tree['right']
return (collapse(ltree) + collapse(rtree))/2
后剪枝的Python实现:
def postprune(tree, test_data):
''' 根据测试数据对树结构进行后剪枝
'''
if not_tree(tree):
return tree
# 若没有测试数据则直接返回树平均值
if not test_data:
return collapse(tree)
ltree, rtree = tree['left'], tree['right']
if not_tree(ltree) and not_tree(rtree):
# 分割数据用于测试
ldata, rdata = split_dataset(test_data, tree['feat_idx'], tree['feat_val'])
# 分别计算合并前和合并后的测试数据误差
err_no_merge = (np.sum((np.array(ldata) - ltree)**2) +
np.sum((np.array(rdata) - rtree)**2))
err_merge = np.sum((np.array(test_data) - (ltree + rtree)/2)**2)
if err_merge < err_no_merge:
print('merged')
return (ltree + rtree)/2
else:
return tree
tree['left'] = postprune(tree['left'], test_data)
tree['right'] = postprune(tree['right'], test_data)
return tree
我们看一下不对刚才的树进行预剪枝而是使用测试数据进行后剪枝的效果:
data_test = load_data('ex2test.txt')
pruned_tree = postprune(tree, data_test)
merged
merged
merged
merged
merged
merged
merged
merged
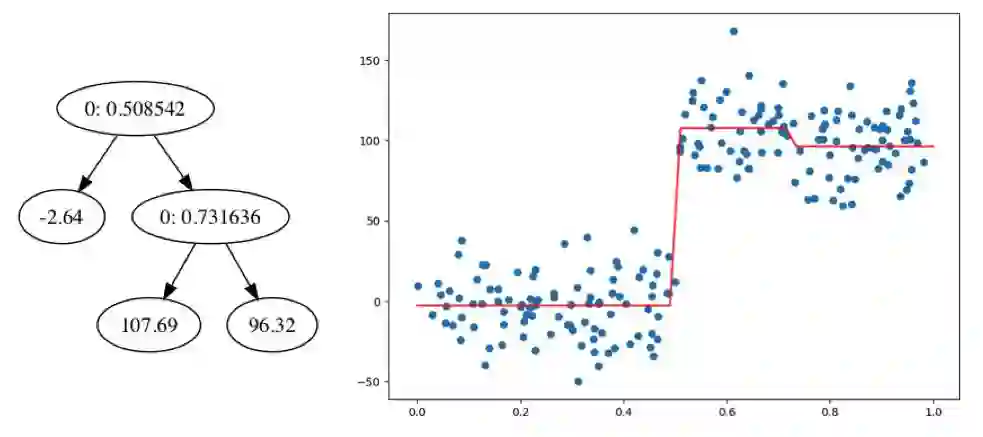
通过输出可以看到总共进行了8次剪枝操作,通过把剪枝前和剪枝后的树可视化对比下看看:
树的规模的确是减小了。
模型树
上一部分叶子节点上放的是分割后数据的平均值并以他作为满足条件的样本的预测值,本部分我们将在叶子节点上放一个线性模型来做预测。也就是指我们的树是由多个线性模型组成的,显然会比强行用平均值来建模更有优势。
模型树使用多个线性函数来做回归比用多个平均值组成一棵大树的模型更有可解释性
而且线性模型的使用可以使树的规模减小,毕竟平均值的覆盖范围只是局部的,而线性模型可以覆盖所有具有线性关系的数据。
模型树也具有更高的预测准确度
创建模型树
模型树和回归树的思想是完全一致的,只是在生成叶子节点的方法以及计算数据误差(不纯度)的方式不同。在模型树里针对一个叶子节点我们需要使用分割到的数据进行线性回归得到线性回归系数而不是简单的计算数据的平均值。不纯度的计算也不是简单的计算数据的方差,而是计算线性模型的残差平方和。
为了能为叶子节点计算线性模型,我们还需要实现一个标准线性回归函数linear_regression, 相应模型树的ferr和fleaf的Python实现
def linear_regression(dataset):
''' 获取标准线性回归系数
'''
dataset = np.matrix(dataset)
# 分割数据并添加常数列
X_ori, y = dataset[:, :-1], dataset[:, -1]
X_ori, y = np.matrix(X_ori), np.matrix(y)
m, n = X_ori.shape
X = np.matrix(np.ones((m, n+1)))
X[:, 1:] = X_ori
# 回归系数
w = (X.T*X).I*X.T*y
return w, X, y
def fleaf(dataset):
''' 计算给定数据集的线性回归系数
'''
w, _, _ = linear_regression(dataset)
return w
def ferr(dataset):
''' 对给定数据集进行回归并计算误差
'''
w, X, y = linear_regression(dataset)
y_prime = X*w
return np.var(y_prime - y)
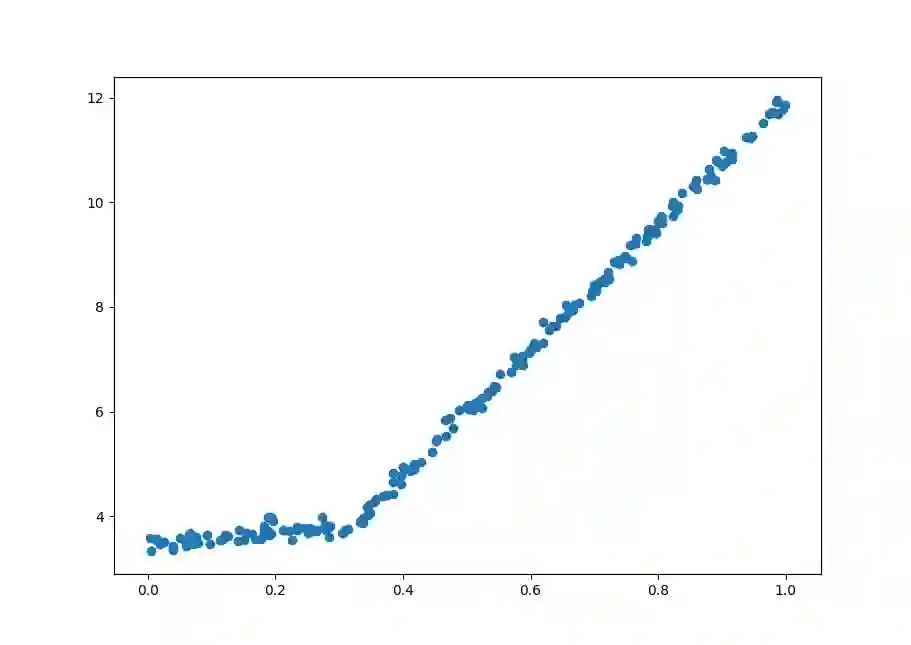
在分段线性数据上应用模型树
本部分使用了事先准备好的分段线性数据来构建模型树,数据点可视化如下:
现在我们使用这些数据构建一个模型树:
tree = create_tree(dataset, fleaf, ferr, opt={'err_tolerance': 0.1, 'n_tolerance': 4})
tree
得到的树结构:
{'feat_idx': 0,
'feat_val': 0.30440099999999998,
'left': matrix([[ 3.46877936],
[ 1.18521743]]),
'right': matrix([[ 1.69855694e-03],
[ 1.19647739e+01]])}
可视化:
绘制回归曲线:
可以通过模型树看到对于此数据只需要两个分支,数的深度也只有2层。
当x<0.304的时候,使用线性模型y=3.47+1.19x来回归
当x>0.304的时候,使用线性模型y=0.0017+1.20x来回归
回归树与线性回归的对比
本部分我们使用标准线性回归和回归树分别对同一组数据进行回归,并使用同一组测试数据计算相关系数(Correlation Coefficient)对两种模型的回归效果进行对比。
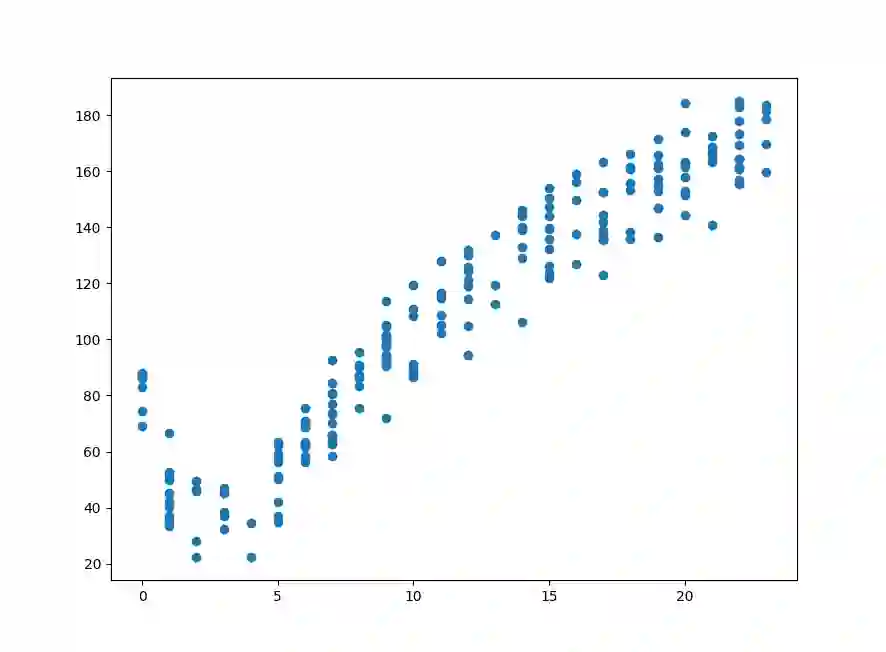
数据我还是使用《Machinie Learning in Action》中的现成数据,数据可视化如下:
现在我们分别使用标准线性回归和回归树对该数据进行回归,并计算模型预测值和测试样本的相关系数R2R2(完整代码见:https://github.com/PytLab/MLBox/blob/master/classification_and_regression_trees/compare.py)
相关系数计算:
def get_corrcoef(X, Y):
# X Y 的协方差
cov = np.mean(X*Y) - np.mean(X)*np.mean(Y)
return cov/(np.var(X)*np.var(Y))**0.5
获得的相关系数:
linear regression correlation coefficient: 0.9434684235674773
regression tree correlation coefficient: 0.9780307932704089
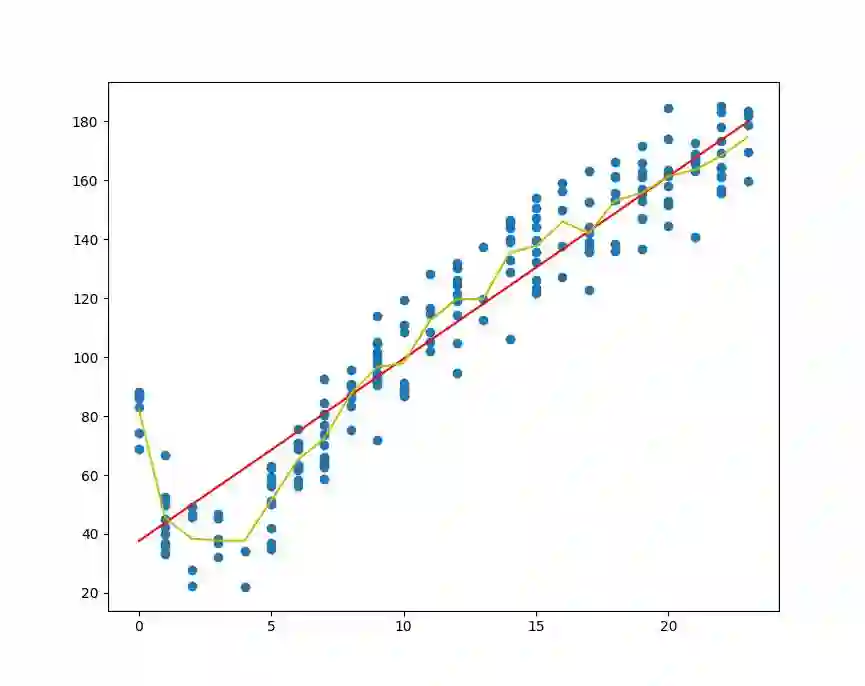
绘制线性回归和树回归的回归曲线(黄色会树回归曲线,红色会线性回归):
可见树回归方法在预测复杂数据的时候会比简单的线性模型更有效。
总结
本文对决策树用于连续数值的回归预测进行了介绍,并实现了回归树, 剪枝和模型树以及相应的树结构输出可视化等。对于模型树也给予了相应的Python实现并针对分段线性数据进行了回归测试。最后并对回归树模型和简单的标准线性回归模型进行了对比。
参考
《Machine Learning in Action》
CART分类与回归树的原理与实现
本系列
看完本文有收获?请转发分享给更多人
关注「大数据与机器学习文摘」,成为Top 1%