数学来了 | 逆矩阵、列空间和零空间怎么回事？我只说一次

“ 我打了几百个响指，也学不好线性代数 ” 

···

···

历史长河里，世世代代的教授和教科书撰写人，总是用荒谬复杂的矩阵计算，掩盖数学真实的简洁模样。

可怕的是，世界上没有什么学科，比线性代数更基础。

计算机科学、物理、电子工程、药物工程、数据科学……数学都是命根子。

我们深知数学带给你的痛苦与无助，从即日起为大家送上这份《线性代数的本质》.avi，试图让你从跟数学战斗的1400万次战斗中，找到胜利的那一种结局。

7

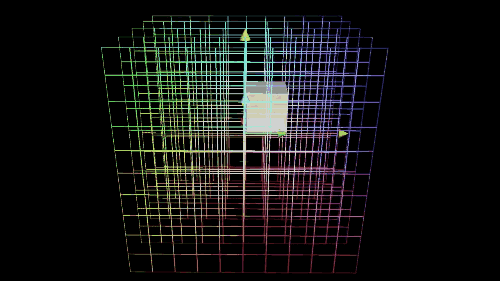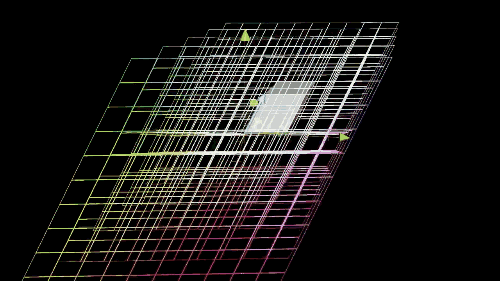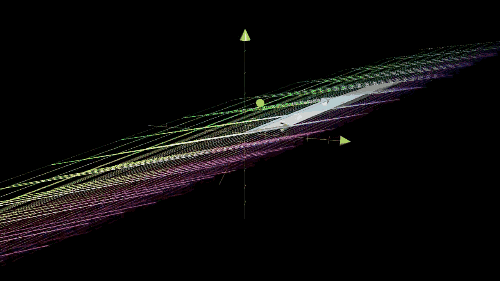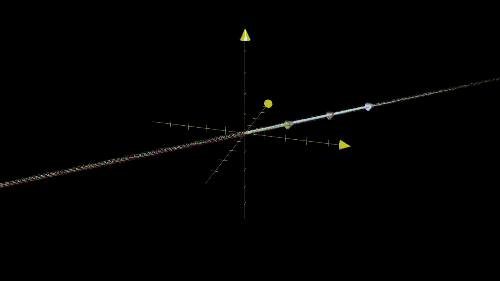
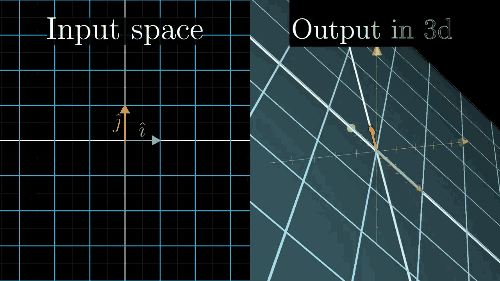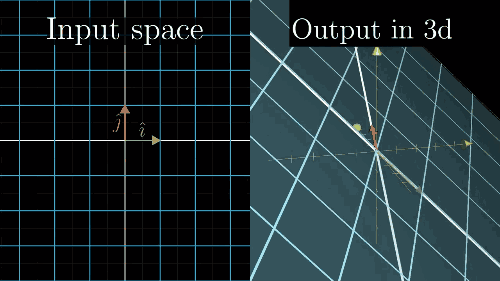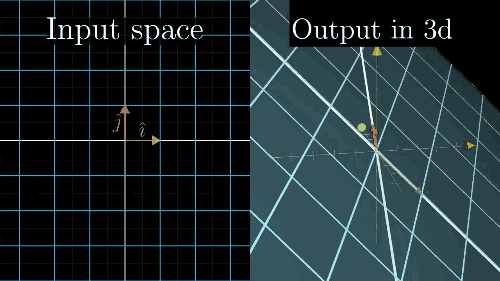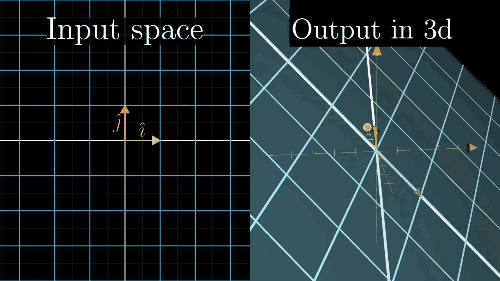
列空间和零空间 (核)

Inverse matrices, column space and null space | Essence of linear algebra, chapter 6

翻译 |  余杭   校对 |  MY

···

下期预告

非方阵矩阵在不同维度上的变换

Nonsquare matrices as transformations between dimensions

图文/视频 via 雷锋字幕组

视频来源 www.3blue1brown.com

斯坦福大学「CS224d：深度自然语言处理课程」中英字幕版

▼▼▼