RPI-IBM团队提出图结构&表征联合学习新范式IDGL：用于图神经网络的迭代式深度图学习

会员服务 ·

RPI-IBM团队提出图结构&表征联合学习新范式IDGL：用于图神经网络的迭代式深度图学习

2020 年 12 月 7 日 将门创投

作者：IBM美国沃森研究中心研究员吴凌飞

NeurIPS 2020 文章专题

第·9·期

本文是RPI-IBM研究团队发表于NeurIPS 2020的一项工作，旨在对数据的图结构和表征进行联合学习，以帮助图神经网络 (GNN) 使用者在图结构未知或存在噪声的情况下，在特定下游任务中取得最优的性能。

本文提出了一个端到端的、迭代式深度图学习框架IDGL，其核心思想是：基于更优的图表征，往往能学到更优的图结构；基于更优的图结构，往往也能学到更优的图表征。这种图结构和表征的联动学习，交替迭代进行，直到图结构 (或表征) 收敛到某种最优值。

基于IDGL框架，研究团队进而开发出一种基于锚定法 (anchor-based) 的扩展版本IDGL-Anch，将算法的时空复杂度从O(n^2)大大降低到O(n)，其中n代表图节点个数。与众多GNN模型和图学习模型相比，本文所提出的模型在9个数据集上取得了最佳或接近最佳的结果。

「NeurIPS 2020群星闪耀云际会·机构专场」已经过半，点击【这里】报名最后三场！

论文链接：

https://arxiv.org/abs/2006.13009

代码链接：

https://github.com/hugochan/IDGL

一、研究问题

图神经网络 (GNN) 可谓是当下机器学习领域 (ML) 最火热的前沿方向之一。自2016年图卷积神经网络 (GCN) 被推出以来，各类新式GNN模型层出不穷，成为各类AI顶级会议的常客。凭借其强大的图表征学习能力，GNN在自然语言处理 (NLP)、计算机视觉 (CV) 、药物发现、推荐系统等众多应用领域取得了一系列重大进展。

GNN虽好，却有一个所有GNN研究和应用人员都必须要面对的问题：使用GNN的一个必要前提是，数据必须被构建成图结构的形式。而在大部分GNN的应用领域中，由于种种原因 (比如存在噪声、图结构不完整等) ，已有的图结构数据对于下游任务而言并不一定是最优的，或者在如NLP等一些应用领域中，数据的图结构往往是未知的。这就带来一个问题，在图结构未知或存在噪声的情况下，如何能用GNN学到足够好的图表征，以期在下游任务中取得最优的结果呢？

这正是RPI-IBM研究团队推出图结构&表征联合学习范式IDGL的初衷。本文所研究的图学习问题可以被定义为如下形式：给定n个节点及描述其属性的特征矩阵，同时可选地给定 (可能存在噪声的) 初始图结构，求最优的图结构和表征，使得模型在特定下游任务中取得最优结果。这里有一点需要额外注意，初始图结构是可选的，在有些应用场景中可能并不可得；而在另一些应用场景中，图结构虽然可得，但对于下游任务而言，可能并非最优。

二、研究背景

这里先简要介绍一下图学习领域的一些已知工作。事实上，不同领域的学者对图结构学习问题都有过广泛研究。例如，在图信号处理和聚类分析领域，研究团队曾尝试过利用不同方式从数据点中直接学习图结构[1,2]。不过这些工作专注于无监督学习，并未考虑到下游任务的需求。另有一些工作专注于概率图模型的结构推理[3]或者图生成[4]问题，与本文所要探究的问题侧重点有所不同。

相较于传统的图结构学习研究，针对GNN的图学习相关研究起步较晚。在对抗机器学习 (Adversarial Machine Learning) 领域，有一系列工作专注于开发更具健壮性的GNN模型[5,6,7]，来对抗针对图结构的各类攻击行为。这类工作一般假设图结构已知，且存在被篡改的可能性，所以需要设法修正被篡改的图结构，从而提高模型在下游任务上的性能。

另外，在CV和NLP领域，也有一些工作尝试为视觉对象或者单词自动化地构建图结构，以期利用GNN模型在下游任务中取得更优结果[8,9]。这些工作主要基于简单的注意力机制学习一个稀疏图结构，但是未对图结构的质量进行过多干预。

近期，ICML 2019有一项工作创造性地提出利用双层优化 (Bilevel Optimization) 技术，针对下游任务，对图结构和表征进行联合学习[10]。它提出的LDS模型在众多数据集上表现优异。但LDS有一个重大缺陷，即无法进行归纳学习，模型必须在训练阶段看到所有的图节点。

最后，图学习问题与Transformer模型[11]亦有所关联。但是Transformer模型一般不考虑已知的图结构，而是利用多头注意力机制，从数据点中直接学习一个全连通的图。

什么！这里竟然有专为技术人设计的免费社交活动？

快点击报名~

本文认为在图学习问题上存在如下挑战：

如何更有效地从图节点特征学习到图结构；
如何针对学到的图结构的质量进行有效控制；
如何使得学到的图结构和表征有助于下游任务；
如何同时支持直推学习 (Transductive Learning) 和归纳学习 (Inductive Learning)；
图结构学习一般需要考虑任意两节点间的关联度，因而对于大图的可扩展性较低，所以，如何降低图结构学习的计算复杂度。

三、迭代式深度图学习框架：IDGL

3.1 核心思想

为了应对上述挑战，本文提出一个端到端的、迭代式深度图学习框架IDGL，旨在对数据的图结构和表征进行联合学习，以帮助图神经网络 (GNN) 使用者在图结构未知或存在噪声的情况下，在特定下游任务中取得最优的性能。

IDGL模型的核心思想如下图所示，即：基于更优的图表征，往往能学到更优的图结构；基于更优的图结构，往往也能学到更优的图表征。这种图结构和表征的联动学习，交替迭代进行，直到图结构 (或表征) 收敛到某种最优值。

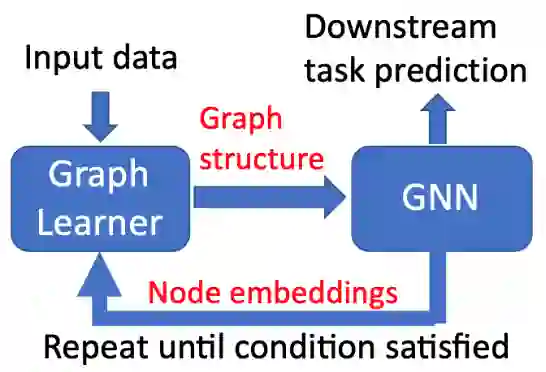
IDGL模型核心思想示意图

3.2 从图节点特征到隐含图结构

研究图节点特征之间的相似度往往能够帮助我们挖掘隐含图结构的秘密。本文借鉴了在Transformer等模型中被广泛使用的多头注意力机制，提出了一种多头加权余弦相似度机制 (权重参数需要学习)，来从图节点特征中学习节点间相似度，进而学习到隐含图结构。由于得到的隐含图是全连通图，本文使用了一种稀疏化方式，进一步从中提取出稀疏隐含图结构。

尽管初始图结构中可能存在噪声，但它往往依然包含着关于最优图结构的丰富信息，所以弃而不用可能并不明智。而对于初始图结构而言，隐含图结构可能会是一个有力的补充，最终帮助模型学到针对特定下游任务的最优图结构。在此基础上，研究团队进一步假设：最优图结构可能是初始图结构上的一个微小“偏移”，进而将初始图结构和学到的隐含图结构合并起来得到最终的图结构。

对于初始图结构不存在的应用场景，研究团队发现基于图节点特征，用简单的余弦相似度计算得到的k-最近邻图来作为初始图结构，在许多应用中都有不错的表现。

3.3 从图结构到图节点表征

一旦有了上面学到的图结构，以及任务给定的图节点特征，后续便可接上GNN模块，从而学到新的图节点表征，进而得到在下游任务上的预测结果。为方便区分，初始的图节点属性编码被称为特征，并经由后续GNN模块转化为表征。

3.4 图结构和表征迭代学习

既然从图节点特征 (或表征) 可以学到图结构，而基于图结构可以学到更好的图节点表征，那么是否可以迭代式地更新图结构和图节点表征，以获得最优的图结构和表征呢？这正是IDGL所采取的优化策略。

IDGL模型系统图

如上图所示，这种图结构和表征的联动学习，交替迭代进行，直到图结构 (或表征) 收敛到某种最优值。而这种联合学习的优化目标是：整体模型在特定下游任务中取得最优的性能。当然，这种迭代式学习过程，通常伴随着一个问题，如何判断何时停止迭代？本文提出了一个有效的动态收敛条件，即当相邻两次迭代中学到的图结构相似度达到一定阈值时，便停止迭代。在原论文中，作者给出了这种收敛存在的条件，并做了实证性分析证明其有效性。

3.5 控制隐含图结构的质量

自然状态下的图结构通常满足一些特性，基于这些特性进行约束往往能获得更高质量的图结构。研究团队通过对模型正则化的方式，进一步对学到的隐含图结构的一些特性进行约束，包括平滑性、连通性、稀疏性。

3.6 混合损失函数

对于隐含图结构的正则化罚项同下游任务上的预测损失一起，共同构成了模型的损失函数。最终模型得以通过反向传播，以端到端的方式进行训练。

四、高可扩展性的图学习模型：IDGL-Anch

由于需要计算任意两图节点间的相似度，IDGL模型的时间复杂度至少是O(n^2)，其中n是图节点个数。是否可以通过某种近似方式来求得隐含图结构，从而降低计算复杂度呢？针对IDGL模型，研究团队优化了隐含图结构学习模块的计算复杂度，开发出一种基于锚定法 (anchor-based) 的扩展版本IDGL-Anch，将算法的时空复杂度从O(n^2)大大降低到O(n)。其核心思想是：将n x n的隐含图邻接矩阵 (Adjacency Matrix) A近似成两个n x s的关联矩阵 (Affinity Matrix) R相乘，即

其中，

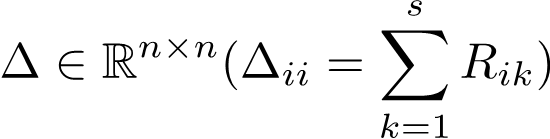
是两个归一化项。

在IDGL-Anch版本中，邻接矩阵A不再被显示地计算，而是通过计算关联矩阵R被隐式地表达。具体计算方式如下：

首先，随机从n个图节点中抽取s (一般远小于n) 个锚定节点，通过上文提到的多头加权余弦相似度机制计算图节点与锚定节点间的关联度，从而得到关联矩阵R。实质上，关联矩阵R代表的是图节点-锚定节点二分图。
在图节点-锚定节点二分图上运行GNN的消息传递机制，即先将节点信息从图节点传递至锚定节点，继而传递回图节点。这个过程被认为是进行了一跳消息传递。
通过对锚定节点图结构的特性进行约束，间接控制隐含图结构的质量。锚定节点图邻接矩阵B可由关联矩阵R计算得到：

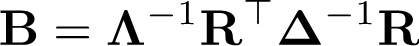
IDGL-Anch将IDGL的时间复杂度从O(Tn^2) 大幅降低到O(Tns^2)，空间复杂度从O(n^2) 大幅降低到O(ns)。其中T代表迭代学习次数。IDGL-Anch这种计算复杂度上的优势在大图上尤为明显。

五、实验结果

5.1 直推学习实验结果

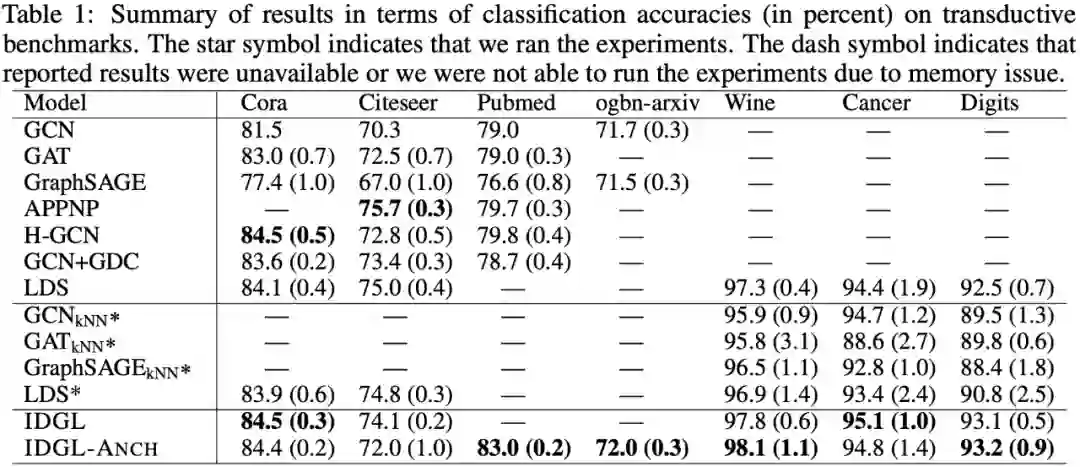
研究团队在7个标准数据集上进行了直推学习实验，即整个数据集只有一张图，在训练阶段即被模型所见。训练集中只包含一部分图节点的类别标签，模型需要在测试集上预测另一部分图节点的类别标签。基线模型包括众多最先进的GNN模型以及图学习模型。同时，研究团队也实现了一些基于k-最近邻图的GNN模型作为图学习基线模型。在7个数据集中，前4个数据集提供了初始图结构，后3个数据集未提供初始图结构。

如下表实验结果所示，IDGL在5个数据集中的4个数据集上，均超过所有基线模型。而相比于IDGL，IDGL-Anch拥有更高的可扩展性，在所有数据集上取得了相当、甚至是更优的结果。当初始图结构未知时，相比于其他图学习模型，IDGL取得了明显更优的结果。

5.2 归纳学习实验结果

尽管图学习基线模型LDS在直推学习实验中也取得了不错的结果，但是LDS无法进行归纳学习。所谓归纳学习，即测试集中包含训练集中所未见的新图。相比而言，如下表所示，IDGL及IDGL-Anch在归纳学习实验中也取得了优异的结果。

5.3 消融实验结果

下表是在几个数据集上进行的消融实验的结果。可以发现，迭代学习模块 (IL) 及图正则化模块 (graph reg.) 都对整体模型性能起到了重要作用。

5.4 健壮性分析结果

为了验证IDGL模型对于对抗性图攻击的健壮性，研究人员对于初始图结构进行了随机增删边篡改攻击。实验结果表明，相比于GCN和LDS，IDGL由于可以利用基于图节点信息学到的隐含图结构，因而拥有更优的健壮性。

在Cora测试集上进行健壮性分析 (增删边)

由于篇幅原因，关于收敛性、收敛停止条件、隐含图可视化等更多实验结果的分析，请参阅原论文。

六、总结及展望

本文提出了一个端到端的、迭代式深度图学习框架IDGL，来实现对图结构和表征的联合学习，以期在特定下游任务中取得最优的性能。为了降低IDGL的计算复杂度，本文进一步提出了一个基于锚定法 (anchor-based) 的扩展版本IDGL-Anch，将算法的时空复杂度从O(n^2)大大降低到O(n)。未来的工作包括探索更有效且高扩展性的隐含图学习机制，以及处理图结构和图节点同时存在噪声的情况。

滑动查看参考文献！

[1]X. Dong, D. Thanou, P. Frossard, and P. Vandergheynst. Learning laplacian matrix in smoothgraph signal representations.IEEE Transactions on Signal Processing, 64(23):6160–6173,2016.

[2]A. Bojchevski, Y. Matkovic, and S. Günnemann. Robust spectral clustering for noisy data:Modeling sparse corruptions improves latent embeddings. InProceedings of the 23rd ACMSIGKDD International Conference on Knowledge Discovery and Data Mining, pages 737–746,2017.

[3] J. Cussens. Bayesian network learning with cutting planes.arXiv preprint arXiv:1202.3713,2012.

[4]R. Liao, Y. Li, Y. Song, S. Wang, W. Hamilton, D. K. Duvenaud, R. Urtasun, and R. Zemel.Efficient graph generation with graph recurrent attention networks. InAdvances in NeuralInformation Processing Systems, pages 4257–4267, 2019.

[5]H. Chen, L. Wang, S. Wang, D. Luo, W. Huang, and Z. Li. Label aware graph convolutionalnetwork–not all edges deserve your attention.arXiv preprint arXiv:1907.04707, 2019.

[6] P. Elinas, E. V. Bonilla, and L. Tiao. Variational inference for graph convolutional networks inthe absence of graph data and adversarial settings.arXiv, pages arXiv–1906, 2019.

[7]J. Klicpera, S. Weißenberger, and S. Günnemann. Diffusion improves graph learning. InAdvances in Neural Information Processing Systems, pages 13333–13345, 2019.

[8]W. Norcliffe-Brown, S. Vafeias, and S. Parisot. Learning conditioned graph structures forinterpretable visual question answering. InAdvances in Neural Information Processing Systems,pages 8344–8353, 2018.

[9]Y. Chen, L. Wu, and M. J. Zaki. Reinforcement learning based graph-to-sequence model fornatural question generation.arXiv preprint arXiv:1908.04942, 2019.

[10] L. Franceschi, M. Niepert, M. Pontil, and X. He. Learning discrete structures for graph neuralnetworks.arXiv preprint arXiv:1903.11960, 2019.

[11] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, andI. Polosukhin. Attention is all you need. InAdvances in neural information processing systems,pages 5998–6008, 2017.

作者介绍：

吴凌飞博士 ，现任IBM T. J. Watson Research Center研究科学家和团队带头人，2016年在威廉玛丽大学取得计算机博士学位。他的研究内容主要包括机器学习、表征学习和自然语言处理。

吴凌飞博士带领的Graph4NLP (Deep Learning on Graphs for Natural Language Processing) 团队 (12+ 研究科学家) 致力于机器学习与文本数据挖掘领域的基础研究，并运用机器学习与文本数据挖掘方法解决实际问题。

其学术成果先后发表在NeurIPS、ICML、ICLR、ACL、EMNLP、KDD、AAAI、IJCAI等国际顶级会议及期刊上，发表论文超过80多篇，代表作包括IDGL、MGMN、Graph2Seq、GraphFlow，并有多项学术论文获得著名国际大会的最佳论文和最佳学术论文奖，包括IEEE ICC 2019。其研究成果被各大媒体报道，包括NatureNews、YahooNews、Venturebeat、TechTalks、SyncedReview、Leiphone、QbitAI、MIT News、IBM Research News和SIAM News.。因其突出的商业和学术贡献，吴凌飞博士带领的Graph4NLP团队获得了IBM Research Research Accomplishment Award (IBM全球1%的最佳团队)，其个人被授予IBM Outstanding Technical Achievement Award (IBM全球最好的1% 员工)。

此外，吴凌飞博士是37项美国专利的发明人，因其专利极为突出的商业价值，吴凌飞博士被IBM 评选为大师发明家 (2020)，全球仅有40名IBM研究科学家被授予此项荣誉。

目前，吴凌飞博士也担任IEEE影响因子最高期刊之一IEEE Transactions on Neural Networks and Learning Systems (TNNLS) 和 ACM SIGKDD 旗舰期刊 ACM Transactions on Knowledge Discovery from Data (TKDD) 的副主编，多次组织国际顶级会议大会并担任主席，如AAAI、IJCAI、KDD、NeurIPS、ICLR、ICML、ACL、EMNLP等。

更多信息请访问个人主页：

https://sites.google.com/a/email.wm.edu/teddy-lfwu/home

-END-

👇

AI人的年底聚会，就差你了！

好吃！好玩！免费！

扫码回复关键词或点击"阅读原文"报名~