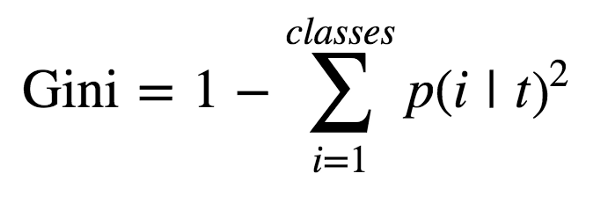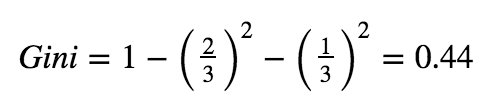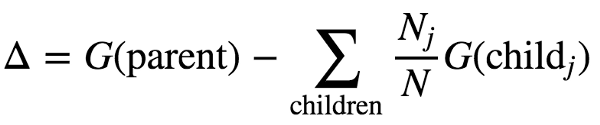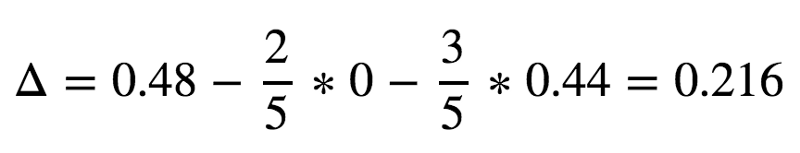决策树：一种像人脑一样工作的算法

2018 年 10 月 12 日 AI研习社

本文为 AI 研习社编译的技术博客，原标题：

Decision Tree: an algorithm that works like the human brain

翻译 | Kyuubi、不到7不改名

校对 | 酱番梨整理 | 志豪

原文链接：

https://towardsdatascience.com/decision-tree-an-algorithm-that-works-like-the-human-brain-8bc0652f1fc6

“从绿叶中穿透的阳光” 来自 Unsplash 的 Jeremy Bishop

决策树是用于机器学习最流行的算法之一，尤其对于分类和回归问题。我们每次做决策时大脑都像决策树一样工作。

比如：“外面是阴天吗？““如果是，我会带一把雨伞”

当我们为了分类变量而训练数据集时，决策树的主要理念是依据确定的特征值把数据分成更小的数据集直到特征变量全部归为一类。另一面，人类大脑决定通常选取基于经验出发的“分支特征”(比如是否阴天)，对于一个计算机分支数据集来说则基于“最大信息增益”。让我们定义一个简单的问题然后切换到一些计算过程去探究其意味着什么！

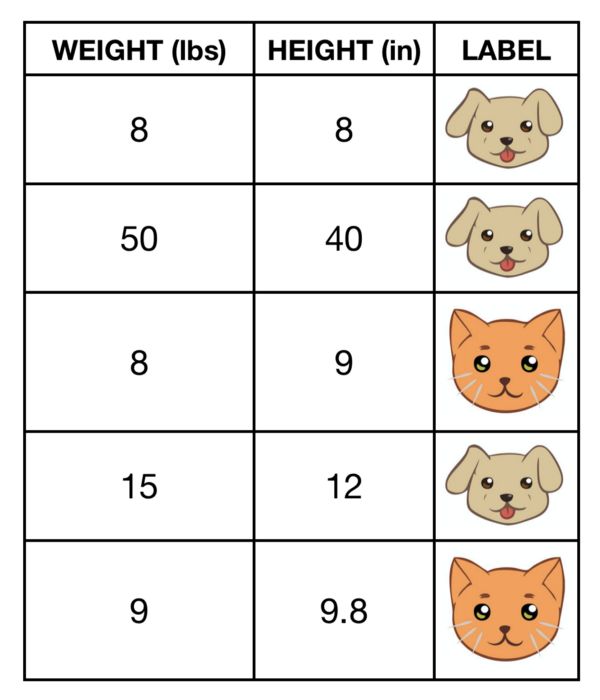
猫和狗构成的数据集

让我们来建立一个决策树：基于高度和重量来决定一个宠物是猫还是狗。

我们会对数据点的两个参数中的一个的确定值进行分类。比如：一个宠物的重量大于15磅，我们会确定这是只狗，至少对于这个简单的数据集来说是这样，但是如果重量小于15磅我们的的子集将会再次分支，其中包含由两只猫所构成的分支和一条狗所构成的分支，直到每个分支中只剩下一类元素，我们绘制了这个过程：

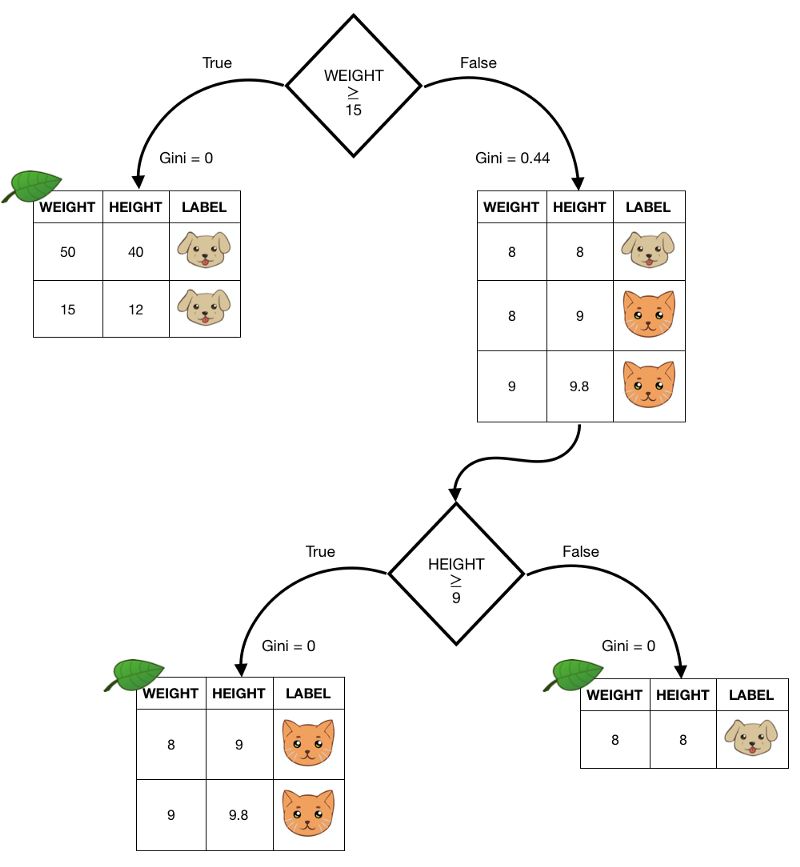
决策树的例子

每棵树开始于根节点，显而易见,从第一个分支出发到一个解，我们可以给出相同步数不同类型的数据分支。

但是计算机会怎样定义节点呢？事实上，为了清楚地理解最有效的方，,我们需要介绍：Gini(不等式的通用测量方法,为了通俗讲本文将Gini中文翻译为基尼系数)。这个不等式提到了单个节点的每个子集中的目标类。因此，它可以在每次分支后计算，并根据计算后不等式的变化去定义“信息增益”。

图为基尼系数的定义

为了计算基尼系数,我们考虑在每一个节点后找到每一类的可能性，对这些值进行求平方之后，用1减去这个值。

出于这个原因,当子集中只有一个类时,基尼系数会为0.因为确实找到一类的可能性是1.在这个例子中,我们给定我们已经到达了叶节点,在这里不需要再进行分支操作了,我们已经达到了目的.但是如果我们看上面的图,当处于根节点之后的False情况下,我们有一个包含三个观测值的子集,两个是猫一个是狗,如果我们想计算这个子集的基尼系数,我们可以:

结果数据集的基尼系数计算重量大于等于15磅.

另一个可以代替基尼系数的测量不等式类别的指标是-熵.(译者注：应该是熵-Entropy,原文中的Entopy少了一个字母).这个指标是出于同样的目的,但是熵的变化比例很小;于是我们只用基尼系数.

根据我们选择的分支策略,我们会有每个子集的基尼系数值,依靠节点后的基尼系数值,我们可以定义信息增益。

信息增益的定义

此定义描述了计算父节点基尼系数和子节点基尼系数加权平均的差.如果我们参考一下上一个例子,使用这个定义可以简单地推导出初始数据集的基尼系数为0.48,则可以计算根节点的信息增益.(分支在重量为15磅时)

根节点后的信息增益值

决策树会考虑所有可能分支的信息增益,并选择一个有最高信息增益的分支。让我们用python实现看看。

通过运行下面的代码，我们只用几行代码来建立一个数据框（通过圆角矩形框表示）的草稿去拟合模型。

注意：

在训练一个模型之前，对于训练、测试分支来说，这是一个很好的练习，去防止过拟合，并且可以双重检验我们的模型在不可见的数据上的表现。

当我们实例化时这是很重要的声明：

DecisionTreeClassifier

我并没有指定任何附带参数。当我们处理非常庞大的数据集时，为了阻止你的树失控和过拟合，非常必要的要定义：

max_depth

为了指定你的树的最大分支层级。同样的必要的定义：

max_features

一个参数限制了预测器的数量去集中于搜索最优的分支。当然如果你想使用熵来代替基尼系数来优化你的树，你只需要写：

criterion = 'entropy'

当实例化了object，如果你想进一步探索如何调整模型，参考决策树模型。

我们建立了我们的模型，但是这究竟意味着什么呢？决策树之美可以很容易的被解释，所以我们把它画出来！为了运行代码段你需要通过pip安装一下package：

pip install pydotplus pydot2

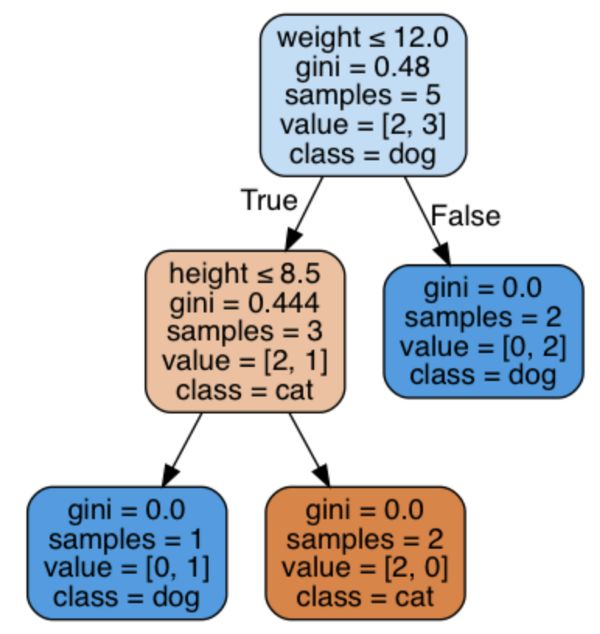
在你的jupyter notebook中代码段的输出会是下面这张图：

很牛逼，对吧~ 尽管在我们的‘手稿’中，我选择了‘15磅重量’作为我的根节点，算法依据同一个变量判断分支，但是对于12这个值则创建了一个只有一条狗的叶节点（对于已有的元素重量大于12磅时，事实上基尼系数为0）。根节点后为真的情况下生成了子集，并且进一步依靠重量变量8.5磅为判断依据进行分支。最后一个分支生成了无基尼系数的两个纯子集。

所以，什么情况下我们应该或者不应该用决策树？这里有一个简短的优缺点的列表：

优点：

拥有很强的可解释性，尤其是我们需要和不懂技术的人员去交流的时候
能够很好地解决噪声数据和不完整数据
可以用于回归和分类问题

缺点：

可能会变得不稳定，也就是说数据集中很小的改变可能导致模型中很大的改变
趋向于过拟合，这意味有着小的偏移但是很大的方差，比如：即使在训练数据上表现很好也无法在更多地不可见测试数据中有同样层次的表现

幸运的是，有很多的技术可以解决过拟合，这是决策树的主要缺点。通过引用bagging或者boosting方法，我们可以从决策树的概念开始，更准确的分析去采用模型，比如：

RandomForestClassifier 或者 AdaBoostClassifier

只先说这两个，这些都是有效的方法，但是随机森林通过 boostrapping 生成了很多新数据集（比如：对源数据帧的拷贝进行采样）；它拟合了树的每一个新的数据帧并且通过均值进行预测森林中的所有树。作为替代的Ada Boost可以自学习，是适应性非常强的树，通过调整不正确的分类实例而永远使用相同的数据帧。