【WWW2021】知识图谱逻辑查询的自监督双曲面表示

知识图谱(KGs)是一些真实应用中普遍存在的信息存储结构，如web搜索、电子商务、社交网络和生物学。由于KGs的规模和复杂性，查询KGs仍然是一个基础性和挑战性的问题。有希望解决这个问题的方法包括在欧几里得空间中嵌入KG单位(如实体和关系)，这样嵌入的查询就包含了与其结果相关的信息。然而，这些方法不能捕获图中实体的层次性质和语义信息。此外，这些方法大多只利用多跳查询(可以通过简单的翻译操作建模)来学习嵌入，并忽略更复杂的操作，如交集和更简单查询的并集。

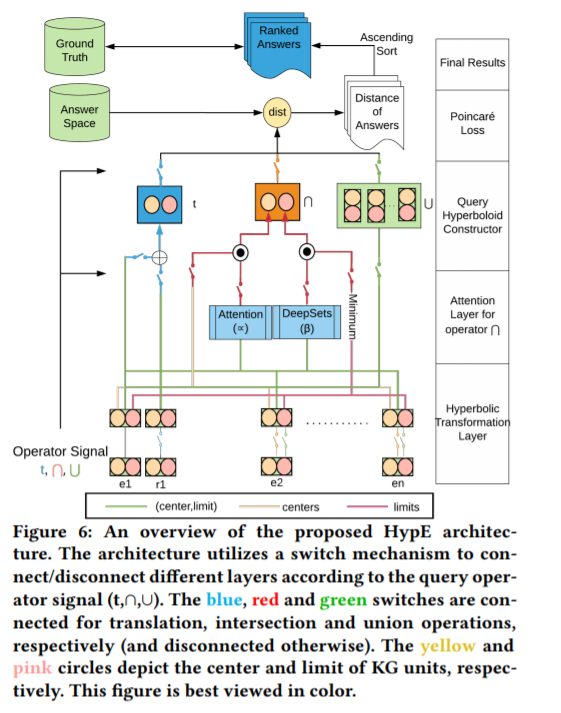
为了解决这些复杂的操作，在本文中，我们将KG表示学习表述为一个自我监督的逻辑查询推理问题，利用KGs上的翻译、交叉和并查询。我们提出了一种新的自我监督动态推理框架——双曲面嵌入(HypE)，它利用KG上的一阶正存在查询来学习其实体和关系在Poincaré球中的双曲面表示。HypE将正面的一阶查询建模为几何平移、交叉和合并。对于真实数据集中的KG推理问题，所提出的HypE模型显著优于最先进的结果。我们还将HypE应用于一个流行的电子商务网站产品分类的异常检测任务，以及分层组织的web文章，并演示了与现有的基线方法相比，显著的性能改进。最后，我们还将学习到的HypE embeddings可视化在Poincaré球中，以清楚地解释和理解表征空间。

https://assets.amazon.science/ec/67/afebbaaf413d856acbff290bc214/self-supervised-hyperboloid-representations-from-logical-queries-over-knowledge-graphs.pdf

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“HYPE” 就可以获取《【WWW2021】知识图谱逻辑查询的自监督双曲面表示》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源