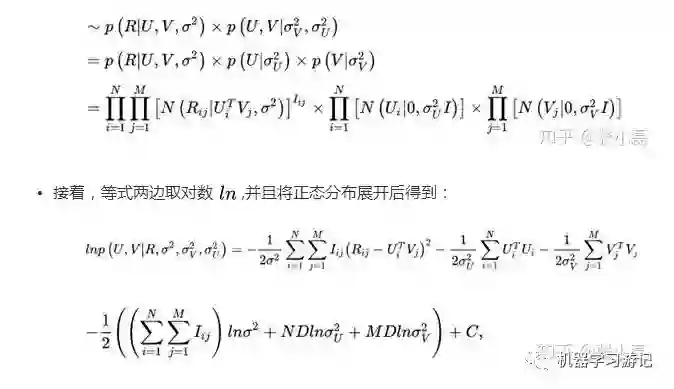极大似然估计与最大后验概率估计
前言
不知看过多少次极大似然估计与最大后验概率估计的区别,但还是傻傻分不清楚。或是当时道行太浅,或是当时积累不够。
这次重游机器学习之路,看到李航老师《统计学习方法》中第一章关于经验风险最小化与结构风险最小化时谈到了极大似然与最大后验的话题,第一反应是竟然在第一章就谈到了极大似然与最大后验,相信大部分初学者看到这两个词时还是怕怕的,毕竟没有太多理论基础。不过没关系,多积累,多搜集相关资料,相信这层疑惑的云雾会逐渐散去的。
这次结合西瓜书和网上大牛的资料,加上自己推荐系统的研究背景以及自己的思考,总算是有些许收获,不虚此行。点滴进步都值得被记录,一来向大家分享,二来谨防遗忘。
频率学派与贝叶斯派
在说极大似然估计(Maximum Likelihood Estimate)与最大后验概率估计(Maximum A Posteriori estimation)之前,不得不说对于概率看法不同的两大派别频率学派与贝叶斯派。他们看待世界的视角不同,导致他们对于产生数据的模型参数的理解也不同。
① 频率学派
他们认为世界是确定的。他们直接为事件本身建模,也就是说事件在多次重复实验中趋于一个稳定的值p,那么这个值就是该事件的概率。
他们认为模型参数是个定值,希望通过类似解方程组的方式从数据中求得该未知数。这就是频率学派使用的参数估计方法-极大似然估计(MLE),这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。
② 贝叶斯派
他们认为世界是不确定的,因获取的信息不同而异。假设对世界先有一个预先的估计,然后通过获取的信息来不断调整之前的预估计。 他们不试图对事件本身进行建模,而是从旁观者的角度来说。因此对于同一个事件,不同的人掌握的先验不同的话,那么他们所认为的事件状态也会不同。
他们认为模型参数源自某种潜在分布,希望从数据中推知该分布。对于数据的观测方式不同或者假设不同,那么推知的该参数也会因此而存在差异。这就是贝叶斯派视角下用来估计参数的常用方法-最大后验概率估计(MAP),这种方法在先验假设比较靠谱的情况下效果显著,随着数据量的增加,先验假设对于模型参数的主导作用会逐渐削弱,相反真实的数据样例会大大占据有利地位。极端情况下,比如把先验假设去掉,或者假设先验满足均匀分布的话,那她和极大似然估计就如出一辙了。
极大似然估计与最大后验概率估计
我们这有一个任务,就是根据已知的一堆数据样本,来推测产生该数据的模型的参数,即已知数据,推测模型和参数。因此根据两大派别的不同,对于模型的参数估计方法也有两类:极大似然估计与最大后验概率估计。
① 极大似然估计(MLE)
-她是频率学派模型参数估计的常用方法。
-顾名思义:似然,可以简单理解为概率、可能性,也就是说要最大化该事件发生的可能性
-她的含义是根据已知样本,希望通过调整模型参数来使得模型能够最大化样本情况出现的概率。
- 在这举个猜黑球的例子:假如一个盒子里面有红黑共10个球,每次有放回的取出,取了10次,结果为7次黑球,3次红球。问拿出黑球的概率 p 是多少?
我们假设7次黑球,3次红球为事件 A ,一个理所当然的想法就是既然事件 A已经发生了,那么事件 A 发生的概率应该最大。所以既然事件 A 的结果已定, 我们就有理由相信这不是一个偶然发生的事件,这个已发生的事件肯定一定程度上反映了黑球在整体中的比例。所以我们要让模型产生这个整体事件的概率最大,我们把这十次抽取看成一个整体事件 A ,很明显事件 A 发生的概率是每个子事件概率之积。我们把 P(A) 看成一个关于 p 的函数,求 P(A) 取最大值时的 p ,这就是极大似然估计的思想。具体公式化描述为P(A)=p^7*(1-p)^3。
接下来就是取对数转换为累加,然后通过求导令式子为0来求极值,求出p的结果。
② 最大后验概率估计(MAP)
-她是贝叶斯派模型参数估计的常用方法。
-顾名思义:就是最大化在给定数据样本的情况下模型参数的后验概率
-她依然是根据已知样本,来通过调整模型参数使得模型能够产生该数据样本的概率最大,只不过对于模型参数有了一个先验假设,即模型参数可能满足某种分布,不再一味地依赖数据样例(万一数据量少或者数据不靠谱呢)。
-在这里举个掷硬币的例子:抛一枚硬币10次,有10次正面朝上,0次反面朝上。问正面朝上的概率p。
在频率学派来看,利用极大似然估计可以得到 p= 10 / 10 = 1.0。显然当缺乏数据时MLE可能会产生严重的偏差。
如果我们利用极大后验概率估计来看这件事,先验认为大概率下这个硬币是均匀的 (例如最大值取在0.5处的Beta分布),那么P(p|X),是一个分布,最大值会介于0.5~1之间,而不是武断的给出p= 1。
显然,随着数据量的增加,参数分布会更倾向于向数据靠拢,先验假设的影响会越来越小。
经验风险最小化与结构风险最小化
经验风险最小化与结构风险最小化是对于损失函数而言的。可以说经验风险最小化只侧重训练数据集上的损失降到最低;而结构风险最小化是在经验风险最小化的基础上约束模型的复杂度,使其在训练数据集的损失降到最低的同时,模型不至于过于复杂,相当于在损失函数上增加了正则项,防止模型出现过拟合状态。这一点也符合奥卡姆剃刀原则:如无必要,勿增实体。
经验风险最小化可以看作是采用了极大似然的参数评估方法,更侧重从数据中学习模型的潜在参数,而且是只看重数据样本本身。这样在数据样本缺失的情况下,很容易管中窥豹,模型发生过拟合的状态;结构风险最小化采用了最大后验概率估计的思想来推测模型参数,不仅仅是依赖数据,还依靠模型参数的先验假设。这样在数据样本不是很充分的情况下,我们可以通过模型参数的先验假设,辅助以数据样本,做到尽可能的还原真实模型分布。
① 经验风险最小化
-MLE她是经验风险最小化的例子。当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化就等价于极大似然估计。在这里举个逻辑回归(LR)的例子,更多跟LR有联系的模型可参看拙作由Logistic Regression所联想到的...。
② 结构风险最小化
-MAP她是结构风险最小化的例子。当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大后验概率估计。 在这里举个推荐系统中的概率矩阵分解(PMF)的例子。
先说下矩阵分解的原理:推荐系统的评分预测场景可看做是一个矩阵补全的游戏,矩阵补全是推荐系统的任务,矩阵分解是其达到目的的手段。因此,矩阵分解是为了更好的完成矩阵补全任务(欲其补全,先其分解之)。之所以可以利用矩阵分解来完成矩阵补全的操作,那是因为基于这样的假设-假设UI矩阵是低秩的,即在大千世界中,总会存在相似的人或物,即物以类聚,人以群分,然后我们可以利用两个小矩阵相乘来还原评分大矩阵。
-这样,我们通过最大后验概率估计推导出了概率矩阵分解的损失函数。可以看出结构风险最小化是在经验风险最小化的基础上增加了模型参数的先验。
MLE与MAP的联系
-在介绍经验风险与结构风险最小化的时候以具体的逻辑回归(LR)与概率矩阵分解(PMF)模型来介绍MLE和MAP,接下里从宏观的角度,不局限于具体的某个模型来推导MLE与MAP。
致谢
至此,频率学派与贝叶斯派,MLE与MAP,经验风险最小化与结构风险最小化的区别与联系已经介绍完毕了,由于本人不是数据专业出身的,并且也是机器学习初学者,难免在叙述或者思考的过程中有不严谨或者不正确的东西,希望大家批判的去看待。
再次感谢以上参考资料以及大牛们的分享。