非凸优化问题综述“从对称性到几何性”，罗切斯特大学等

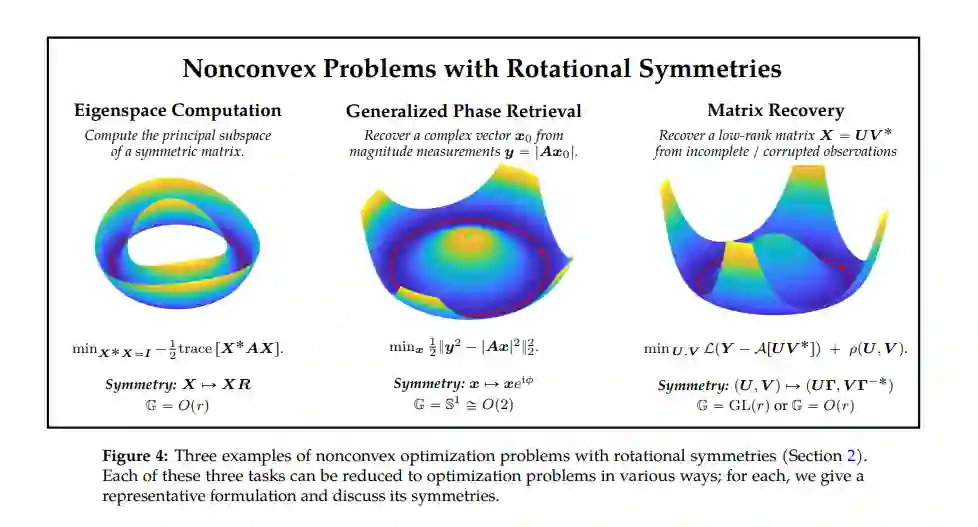
随着科学与工程越来越多地由数据驱动，优化的作用已经扩展到几乎数据分析流水线的每一个阶段，从信号和数据采集到建模和预测。实际中遇到的优化问题往往是非凸的。虽然挑战因问题而异，但非凸性的一个常见来源是数据或测量模型中的非线性。非线性模型通常表现出对称性，创造出复杂的、非凸的客观视角，具有多个等价解。然而，简单的方法(如梯度下降)在实践中往往表现得非常好。这一综述的目的是突出一类可处理的非凸问题，可以通过对称性的视角来理解。这些问题呈现出一种典型的几何结构:局部最小值是单一“真值”解的对称副本，而其他临界点出现在真值解的对称副本的平衡叠加处，并在打破对称性的方向上表现出负曲率。这种结构使有效的方法获得全局最小值。我们讨论了在成像、信号处理和数据分析的广泛问题中产生的这种现象的例子。我们强调了对称在塑造客观视角中的关键作用，并讨论了旋转对称和离散对称的不同作用。这一地区有很多观察到的现象和悬而未决的问题;最后，我们强调了未来研究的方向。

https://www.zhuanzhi.ai/paper/563b993d68765c866b344a88f977515f

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“SGNP” 就可以获取《非凸优化问题综述“从对称性到几何性”，罗切斯特大学等》专知下载链接

                       

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取100000+AI(AI与军事、医药、公安等)主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取100000+AI主题知识资料