DeepMind 再发 Nature,图神经网络解决物理难题
编译 | 蒋宝尚

固体理论中最深奥、最有趣的未解决的问题可能是关于玻璃的性质和玻璃转变的理论。
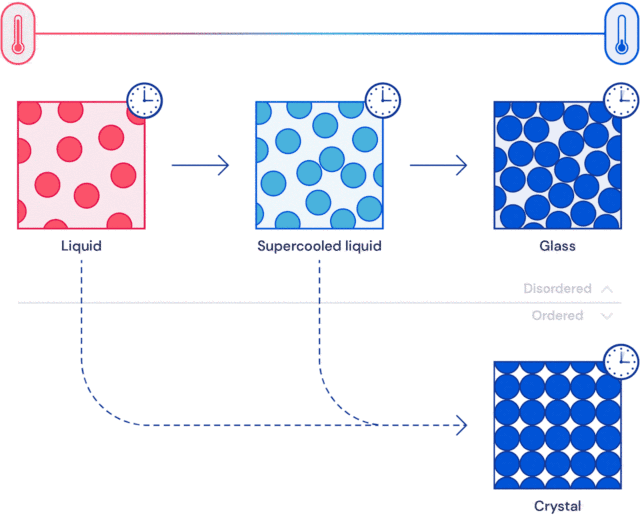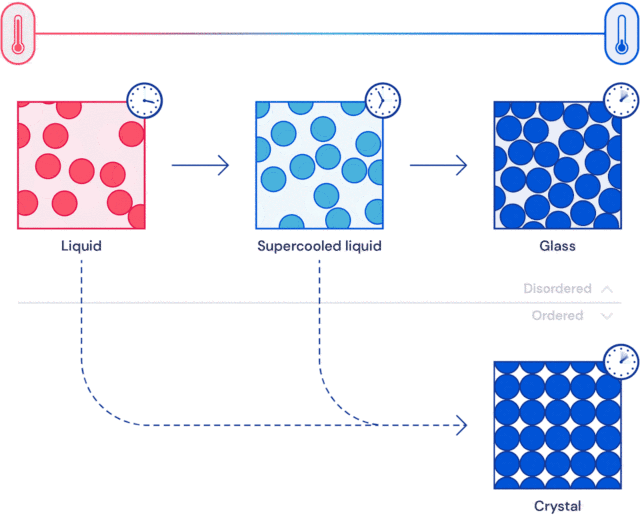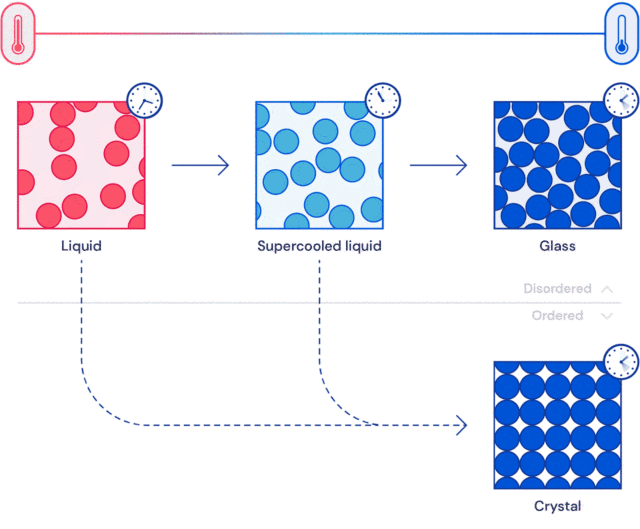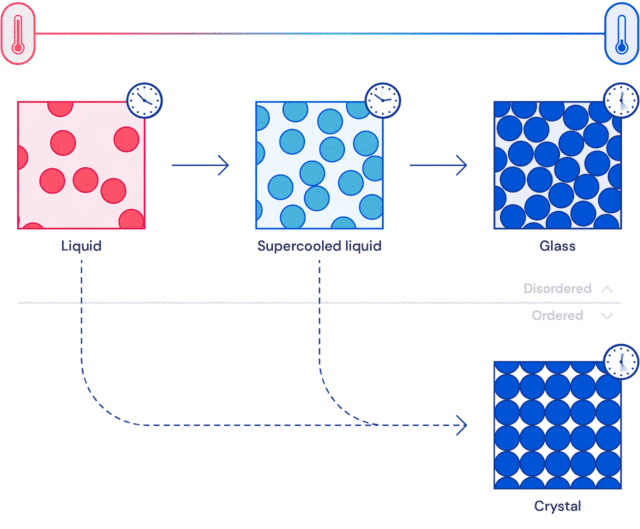
模拟玻璃的实际意义
用图神经网络建模玻璃动力学
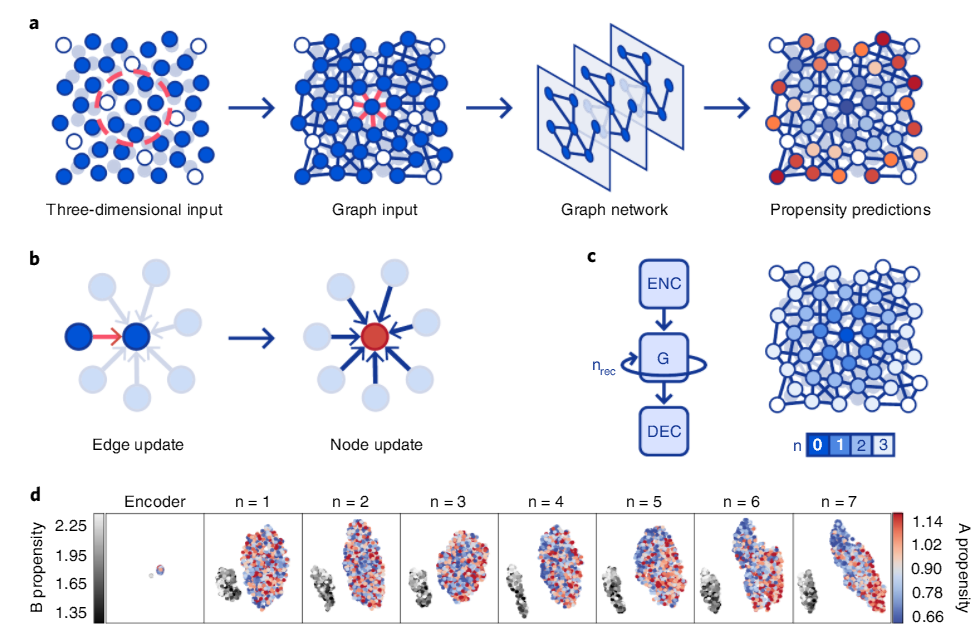
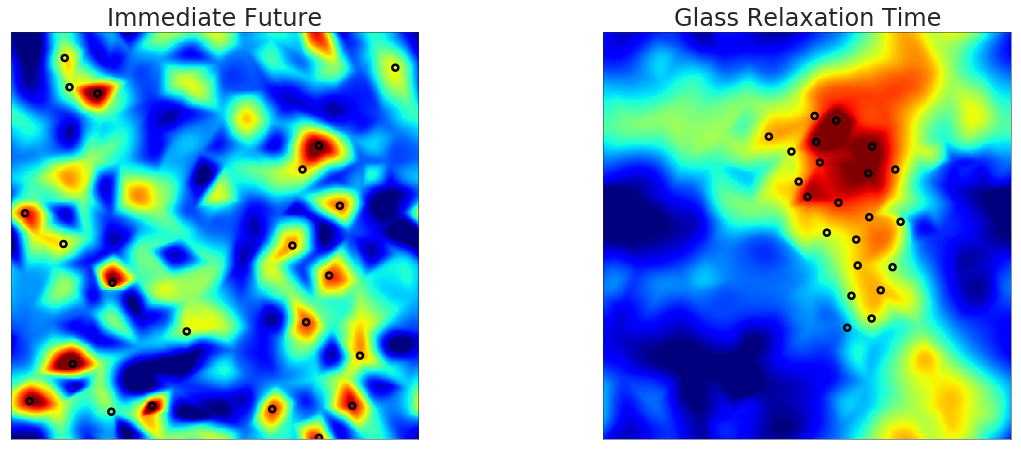
将网络预测与物理联系起来
结语
点击「阅读原文」,直达直播地址👇
登录查看更多
编译 | 蒋宝尚
固体理论中最深奥、最有趣的未解决的问题可能是关于玻璃的性质和玻璃转变的理论。

模拟玻璃的实际意义
用图神经网络建模玻璃动力学
将网络预测与物理联系起来
结语
点击「阅读原文」,直达直播地址👇