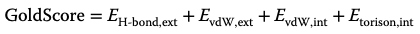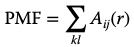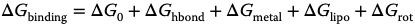药物化学第二期：蛋白质-小分子对接Score函数总结

评分函数是用于预测非共价蛋白质-配体相互作用强度的数学表达式。它们涉及三种不同的应用场景：对接中的姿势预测，虚拟筛选中化合物的排名和结合亲和力的预测。

姿势预测的挑战是从对接算法提供的众多建议中识别配体在蛋白质活性位点内的自然结合模式。主要应用是虚拟筛选中化合物的排名，旨在区分生物活性物质和非活性物质。

评分函数最苛刻的应用是结合亲和力预测，因为必须考虑许多不同的分子相互作用，力和效应并相互平衡。根据16种不同评分函数管理这三项任务的能力，可以在Cheng等人的综述中找到[2]。他们的结论是，今天的评分函数在姿势预测方面相当不错，但在排名和绑定亲和力预测方面仍需要改进。

所有评分函数的物理化学基础是预测蛋白质-配体结合的过程中吉布斯自由能（Gibbs free energy, ΔG）的变化。结合时，形成的复合物的能量低于单独两个分子的能力之和；它是一个自发的过程，因此是负值。吉布斯自由能可以通过吉布斯-亥姆霍兹方程（Gibbs-Helmholtz equation)计算：

ΔG = ΔH − TΔS

ΔH和ΔS分别是焓和熵的变化，T是开尔文的绝对温度。焓部分（ΔH）主要由配体和蛋白质之间的范德华，静电和氢键相互作用组成，通常通过评分函数进行建模。

相比之下，由于对潜在效应进行建模的挑战，熵部分（TΔS）经常被忽视。由配体结合引起的无序水分子从结合位点释放和两个分子扭转角的冻结是熵的两个方面。只有后者被一些经验评分函数明确的修饰了[3，4]。

当前评分函数中描述的最常见的非共价键相互作用是氢键，盐桥，金属相互作用，范德华相互作用，芳香族相互作用和疏水效应。氢键是有向相互作用，考虑到相互作用长度和角度，具有明显的最小值[5].氢键的先决条件是氢键供体和受体的去溶剂。由于极性原子的去溶剂是一个高能成本密集型过程，因此重要的是蛋白质-配体界面中埋藏的极性原子饱和。

前面讨论的大多数相互作用在蛋白质-配体结合过程中起着重要作用，并且通常在评分函数中建模为藐视不同相互作用的单个术语的总和。

打分函数可以3中不同的类型：

1 基于力场的评分函数

基于力场的评分函数使用经典的分子力场来估计蛋白质-配体复合物中的相互作用。扭转能，伦纳德-琼斯势能和静电是在分子力学力场中计算的常见能量，如Amber[6](设计用于蛋白质）或MMFF[7]（设计用于小分子）。

对原子进行分类，生成的原子类型用于校准系统的参数。这些评分函数通常用于在姿势构建过程中指导对接算法。GoldScore [7， 8] 就是这种基于力场的评分函数的一个例子。它由以下四项组成

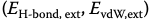
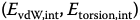
计算蛋白质和配体之间的范德华和氢键能以及范德华和配体的扭转应变能。基于力场的评分函数的优势在于姿态预测，而不是排名或结合亲和力预测，因为缺少考虑熵的项以及静电相互作用和氢键的过拟合。

2 基于知识的评分函数

基于知识的评分函数利用了不断增长的实验高分辨的分离的蛋白质-配体复合物结构。这些评分函数依赖于通过对蛋白质-配体复合物中发生的常见相互作用/距离的统计分析计算成对原子电位。

最终分数计算为一定距离截止范围内的所有原子对的电位值之和。这里的缺点是对于罕见的相互作用，如cation-π或卤素相互作用，没有很好地参数化。这种评分函数的一个例子是平均力的势能(potential of mean force)：

Aij是蛋白质 - 配体原子对相互作用在距离r处的自由能，kl是ij型的配体 - 蛋白质原子对。PMF功能由Muegge和Martin[9]开发，并于2006年在蛋白质 - 配体晶体结构（来自PDB的7152个蛋白质 - 配体复合物）的大型数据集上重新参数化[10]。

这类评分函数的其他例子是DrugScorePDB [11]或DrugScoreCSD [12]，它们来自剑桥结构数据库中PDB和小有机分子的蛋白质 - 配体复合物的统计分析[13]。

3 基于经验评分函数

基于经验评分函数是最常见的评分函数类型。结合自由能是由蛋白质-配体复合物中发现的不同物理化学效应项的计算总和得到，例如氢键，疏水效应或金属相互作用。这些评分函数通常根据实验测量的具有已知结构的复合物的结合亲和力进行校准。

这种类型的第一个评分函数是由Boehm[14]开发的。Boehm的功能进一步发展到广泛使用的ChemScore[15]功能，其原始版本如下所示：

ΔG结合是估计的自由结合能。氢键（ΔG hbond），金属相互作用（ΔGmetal），亲脂性相互作用（ΔGlipo）以及惩罚配体灵活性的项（ΔGrot）。常数项 （ΔG0） 在实际测量结合的校准过程中出现。

最初的ChemScore使用了一组由82种蛋白质 - 配体复合物组成的训练集，这些复合物具有已知的结合亲和力和来自PDB的可靠结合几何形状。这种类型的另一个众所周知的评分函数是X-Score评分函数[16]。经验评分函数的最大缺点是，它们在接近校准数据集中使用的蛋白质家族上表现更好[17]。

其它评分函数

除了适合上述三个类别之一的评分函数外，还开发了估计自由结合亲和力的替代方法。其中一些方法试图以更直接的方式对基础物理场进行建模。它们不对蛋白质-配体结构的评分函数进行校准，也不测量结合亲和力，因此评分函数更通用。

Kel-logg等人开发了HINT相互作用力场[18]，该力场由1-辛醇/水的分配系数（log P）推导出来。它包括氢键、静电相互作用、疏水接触、熵和溶剂化/溶解。HYDE [19， 20] 评分函数还使用小分子的对数 P 值进行校准。它始终如一地描述了蛋白质-配体复合物中的氢键、疏水效应和去溶剂。

另一种策略是专门为一个系统训练评分函数，这些方法被称为定制或针对特定目标的评分函数[21]。在这里，评分函数在特定蛋白质靶标的已知配体或晶体结构上进行校准，因此该靶标的预测能力增加。

缺点是，当只有有限信息的新药设计项目开始时，不能使用这种方法。在开发过程中，它可用于对彼此之间的引线进行排名，以及识别新的有前途的分子。一个例子是ISAC方法[22]，它使用活动悬崖的信息来推导药效团假设和目标特异性评分函数。

在蛋白质 - 配体复合物评分中获得更可靠结果的另一种选择是使用所谓的共识评分。该策略结合了不同现有评分函数的结果，以获得更可靠的预测[23]。虽然可靠性通常会提高，但共识评分通常也会减少已识别的真实活性物质的数量[24]。

其他计算要求更高的方法，如分子力学泊松-玻尔兹曼/广义出生表面积（MM-PB/ GBSA），用于蛋白质 - 配体复合物的重新评分。这些评分函数更基于物理，结合了短分子动力学模拟运行，以考虑系统的灵活性和分子表面的变化，以计算去溶剂效应。

Brown和Muchmore[25]通过他们的MM-PBSA方法显示出有希望的结果，在实验亲和力和预测分数之间实现了良好的相关性。对于三个测试数据集，皮尔逊相关系数 （R） 在 0.72–0.83 的范围内。然而，这些方法在计算上仍然过于昂贵，无法在大规模虚拟筛选的背景下应用它们。

这同样适用于自由能计算方法，如自由能扰动（FEP）或热力学积分（TI [26]），这些方法最近引起了更多的兴趣（有关评论，请参阅Chipot和Pohorille [27]）。这些方法计算与同一蛋白质靶标结合的相似配体之间的相对能量差，以估计结合亲和力。通过更彻底地模拟底层系统（蛋白质 - 配体复合物），这些方法似乎是简单评分函数的有前途的替代方案。然而，它们提供了巨大的专业知识来获得可靠的结果[28]。

由于水分子在结合过程中的重要性，最近开发了新的方法来显式建模和分析结合口袋中的水分子。例如，WaterMap [29， 30]使用显式水分子的分子动力学模拟来识别模拟中结合口袋中水密度高和低的区域。它进一步估计了这些水分子的焓和熵。因此，它可以帮助决定哪些水分子可以被替换，从而获得结合能。

另一方面，高分辨率X射线晶体学的实验数据可用于统计分析蛋白质 - 配体复合物中的水分子。这里的一个挑战是只包括具有实验证据的水分子，这意味着测量的电子密度。最近开发了一种名为EDIA的新型描述符[31]，用于定量评估这些小分子的电子密度的质量。

参考文献

[1] Applied Chemoinformatics Achievements and Future Opportunities-Wiley-VCH(2018)

[2] Cheng, T., Li, X., Li, Y., and Wang, R. (2009) J. Chem. Inf. Model., 49,1079–1093.

[3] Böhm, H.J. (1994) J. Comput.-Aided Mol. Des., 8, 243–256.

[4] Eldridge, M.D., Murray, C.W., Auton, T.R., Paolini, G.V., and Mee, R.P.(1997) J. Comput.-Aided Mol. Des., 11, 425–455.

[5] Gilli, G. and Gilli, P. (2009) The Nature of the Hydrogen Bond, Oxford Uni-versity Press.

[6] Sarwar, M.G., Dragisic, B., Salsberg, L.J., Gouliaras, C., and Taylor, M.S.(2010) J. Am. Chem. Soc., 132, 1646–1694.

[7] Verdonk, M.L., Cole, J.C., Hartshorn, M.J., Murray, C.W., and Taylor, R.D.(2003) Proteins, 52, 609–623.

[8] Mooij, W.T.M. and Verdonk, M.L. (2005) Proteins Struct. Funct. Bioinf., 61,272-287.

[9]  Muegge, I. and Martin, Y. (1999) J. Med. Chem., 42, 791–804.

[10] Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H.,Shindyalov, I.N., Bourne, P.E. (2000) Nucleic Acids Res., 28, 235–242. doi:10.1093/nar/28.1.235

[11] Gohlke, H., Hendlich, M., and Klebe, G. (2000) J. Mol. Biol., 295, 337–356.

[12]  Velec, H.F.G., Gohlke, H., and Klebe, G. (2005) J. Med. Chem., 48,6296–6303.

[13] Groom, C. R., Bruno, I. J., Lightfoot, M. P., Ward, S. C. (2016) Acta Cryst.,B72,171–179, DOI: 10.1107/S2052520616003954

[14] Böhm, H.J. (1994) J. Comput.-Aided Mol. Des., 8, 243–256.

[15]  Eldridge, M.D., Murray, C.W., Auton, T.R., Paolini, G.V., and Mee, R.P.(1997) J. Comput.-Aided Mol. Des., 11, 425–455.

[16] Wang, R., Lai, L., and Wang, S. (2002) J. Comput.-Aided Mol. Des., 16, 11–26.

[17] Perola, E., Walters, W.P., and Charifson, P.S. (2004) Proteins, 56 (2), 235–249.

[18] Kellogg, G.E., Burnett, J.C., and Abraham, D.J. (2000) J. Comput.-Aided Mol.Des., 15 (4), 381–393.

[19] Reulecke, I., Lange, G., Albrecht, J., Klein, R., and Rarey, M. (2008) ChemMedChem, 3 (6), 885–897.

[20] Schneider, N., Lange, G., Hindle, S., Klein, R., and Rarey, M. (2013) J. Comput.-Aided Mol. Des., 27, 15–29.

[21] Seifert, M.H.J. (2009) Drug Discovery Today, 14, 562–569.

[22]  Seebeck, B., Wagener, M., and Rarey, M. (2011) ChemMedChem, 6,1630–1639.

[23] Yang, J.M., Chen, Y.F., Shen, T.W., Kristal, B.S., and Hsu, D.F. (2005) J.Chem.Inf. Model., 45, 1134–1146.

[24] Stahl, M. and Rarey, M. (2001) J. Med. Chem., 44, 1035–1042.

[25] Brown, S.P. and Muchmore, S.W. (2009) J. Med. Chem., 52, 3159–3165.

[26]  Kirkwood, J.G. (1935) J. Chem. Phys., 3, 300–313.

[27] Chipot, C. and Pohorille, A. (2007) in Springer Series in Chemical Physics,Free Energy Calculations: Theory and Applications in Chemistry and Biol- ogy, vol. 86 (eds C. Chipot and A. Pohorille), Springer-Verlag, Berlin, pp. 33–75.

[28] Michel, J. and Essex, J.W. (2010) J. Comput.-Aided Mol. Des., 24, 639–658.

[29] Abel, R., Young, T., Farid, R., Berne, B.J., and Friesner, R.A. (2008) J. Am.Chem. Soc., 130, 2817–2831.

[30] Young, T., Abel, R., Kim, B., Berne, B.J., and Friesner, R.A. (2007) Proc. Natl.Acad. Sci. U.S.A., 104, 808–813.

[31] Nittinger, E., Schneider, N., Lange, G., and Rarey, M. (2015) J. Chem. Inf.Model., 55 (4), 771–783.