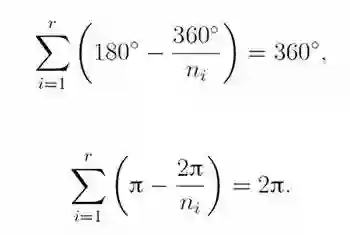直觉与抽象齐飞，浅近共深奥一色丨组合几何趣谈

2017 年 11 月 9 日 科学出版社 丁仁

组合几何是一门融组合论与几何学为一体的学科，研究几何元素的离散性质，研究几何元素的各种组合配置问题与相关计数问题。这里的所谓几何元素包括诸如点、直线、圆、球面、多边形、多面体等我们熟悉的几何对象。

许多组合几何问题因其直观浅近的表述独具魅力，而问题的解决却往往或抽象深奥，或峰回路转，套用王勃《滕王阁序》中的名句，真可谓“直觉与抽象齐飞，浅近共深奥一色”。正如匈牙利数学家Pach在他的《组合几何》中文版序中所说，“组合几何学中尚未解决的难题比比皆是，解决这些问题需要新思想与新方法，组合几何学是有志挑战数学难题者一展身手的最佳领域”。鉴于这一领域的研究难度与论证方法的多样性，许多具体问题的解决往往标志着相关研究课题的重要进展。

组合几何学是一个古老而又年轻的数学分支。事实上德国数学家欧拉(1667—1748)与开普勒(1571—1630)即对组合几何问题多有研究但严格说来组合几何作为一个数学分支是从20世纪30年代开始逐步形成的，保罗·埃尔德什(1913—1996)不断提出大量组合几何问题，引起了数学界的越来越广泛的关注，20世纪中叶开始涌现出多种多样的组合几何研究成果。埃尔德什一生发表了约1500篇高水平的学术论文，提出过组合几何及其他数学分支不计其数的猜想与待解决问题，被称为20世纪的欧拉，罕见的数学奇才。埃尔德什以在全世界发掘和培养数学天才为己任，造就了一大批贡献卓著的数学家。埃尔德什没有家室，没有职位，居无定所，四海为家，把一生献给了数学，去世前几小时还在华沙一个学术会议上讨论数学问题。埃尔德什常风趣地说，“在天国上帝保存着一部巨著，其中有对一切数学问题的解答，有朝一日我见到那部巨著，不知会读到些什么结果”。

组合几何这个名称起源于1955年H.Hadwiger等出版的题为《平面组合几何》(Der kombinatorischen Geometrie in der Ebene)的专著。国际数学界公认，这部专著是组合几何学作为一门新学科诞生的标志。在凸集理论与组合几何学等领域作出重大贡献的美国著名数学家Victor Klee(1925—2007)将其由德文原版译成英文，并添加反映最新成果的一章，于1964年出版，堪称组合几何发展史上的一大盛事。

事实表明，许多离散与组合几何研究成果在编码理论、组合优化理论、机器人学、计算机图形学等诸多领域都有十分重要的应用。计算机技术的迅猛发展为组合几何的研究提供了强大的动力与契机;而组合几何的研究成果又为计算机科学与数学有关研究提供了重要工具，使组合几何学的理论与实际应用价值更为突出。2015年7月29日美国华盛顿大学的研究人员Casey Mann，Jennifer McLoud与David Von Derau利用算法理论并借助计算机发现了一百年以来第十五种可以铺砌平面的凸五边形，堪称是这种相辅相成关系的极好佐证。正如Boltyanski等数学家1997年在他们的一部有关组合几何学的专著中指出的，“泛函分析、经济数学、优化理论、博弈论等学科在深入研究进程中必须建立确切的几何形象或几何模型”，组合几何—离散几何—凸几何理论已成为现代应用数学的重要工具之一。

精彩书摘

铺砌的艺术

铺砌的艺术，或称镶嵌的艺术，在文明史中可以说是源远流长。远古时代当人们开始建造房屋时，就想到要用石块覆盖地面或美化墙壁，要选择石块的颜色与形状，要让石块镶嵌得当，创造一个舒适美观的环境；这时在他们的心目中就有了我们今天说的“铺砌”或“镶嵌”，可以毫不夸张地说铺砌是一种艺术。荷兰画家M.C.Escher(1898-1972)，被称为20世纪画坛中独树一帜的艺术家，以其源自数学灵感的木刻、版画等作品而闻名世界。图1是Escher的名作《飞马图》，用一幅飞马图案形成的区域铺砌全平面，不重叠，无空隙。Escher创作了大量这样的作品，所以艺术界也称他为“铺砌艺术之王”(king of tessellation art)。著名英国数学家Roger Penrose在铺砌理论方面有突出成就，也是一位铺砌艺术家，他与Escher在阿姆斯特丹一次数学学术会议上结识，在数学研究与艺术创作上多有合作，相得益彰，传为佳话。我们这里只讨论用正多边形铺砌平面的相关问题。

图1 Escher的名作《飞马图》

图2

图3

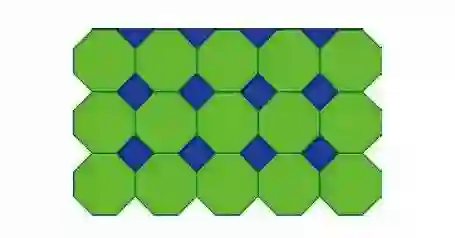
在日常生活中经常会见到单一用正三角形、正方形或正六边形瓷砖铺砌的地面，无重叠，无空隙，如图2所示，抽象地说，单一用正方形可以铺砌全平面，无重叠，无空隙。正三角形与正六边形也如此。另一情形是，可同时使用几种不同正多边形铺砌全平面，如图3所示。

现讨论用正多边形铺砌平面的问题。首先引入一些基本概念与术语。

铺砌元 用来铺砌全平面的多边形称为铺砌元。铺砌元铺砌全平面既无重叠也无间隙，即所谓“不重不漏”。

铺砌的顶点和边 平面铺砌中有限个多边形铺砌元如有公共部分，即如有非空交，则非空交或是孤立点，或是多边形的边。前者称为铺砌的顶点，后者称为铺砌的边。如果若干铺砌元交于同一铺砌顶点，则称这些铺砌元与该铺砌顶点相关联。

图4

边对边铺砌 若平面铺砌的顶点和边均是铺砌元的顶点和边，反之，每个铺砌元的顶点和边也都是铺砌的顶点和边，则称这样的平面铺砌为边对边铺砌。易知在边对边铺砌中，每个铺砌元的边恰好是另一个铺砌元的边。图4(a)显示的是由正方形构成的边对边铺砌，图4(b)显示的则是由正方形构成的非边对边铺砌。

铺砌的顶点特征 平面铺砌中与铺砌顶点关联的铺砌元(正多边形)的边数与邻接顺序构成该铺砌顶点的顶点特征。若与某个顶点关联的r个正多边形的边数依顺时针方向为n₁；n₂；···；n_r，则该顶点的顶点特征用有序正整数数组(n₁；n₂；···；n_r)表示。例如图2中显示的三个铺砌其顶点特征依次是(3；3；3；3；3；3)；(4；4；4；4)；(6；6；6)，可依次简记为(3⁶)；(4⁴)；(6³)；图3中的铺砌其顶点特征则是(4；8；8)，可简记为(4；8²)。

阿基米德铺砌 满足下列条件的铺砌称为阿基米德铺砌，又称齐次铺砌(homogeneous tiling)：铺砌元均为正多边形；铺砌是边对边铺砌；铺砌各顶点的顶点特征相同，与每个铺砌顶点关联的正多边形内角和均为360°。

360°条件 对阿基米德铺砌而言，其各顶点的顶点特征相同，所以可用表示铺砌顶点特征的有序数组来表示该铺砌。平面铺砌中各个铺砌元即正多边形彼此无交叠，无间隙，对每个铺砌顶点而言，与其关联的各多边形对该顶点贡献的内角和是360°。设有序正整数数组(n₁；n₂；···；n_r)表示一个阿基米德铺砌的顶点特征，则该数组必满足下述条件：

为叙述简便，称之为360°条件。但满足360°条件的有序数组未必是一个铺砌的顶点特征，例如有序数组(3；7；42)显然满足360°条件，但不是铺砌的顶点特征，后面我们会详细论述这个问题。

本文摘编自丁仁著《组合几何趣谈》文前及第一章，内容有删减。

组合几何趣谈

（七彩数学/姜伯驹主编）

丁仁著

责任编辑: 陈玉琢

北京：科学出版社 2017.09

ISBN 978-7-03-054077-5

《组合几何趣谈》介绍一系列典型而有趣的组合几何问题. 全书论述力求深入浅出, 周密详尽, 配有大量插图, 以便读者思考理解; 《组合几何趣谈》既注重问题的趣味性, 又不失推理严谨, 体现了组合几何这门学科的特点,可谓“直觉与抽象齐飞, 浅近共深奥一色”.书中大部分命题定理均给出浅近完整的证明, 有的命题还给出多种证明, 以触类旁通, 开阔思路. 各个章节的内容具有相对独立性, 读者可选择感兴趣的章节先行阅读, 开篇有益, 随后必有兴趣细读全书, 提升对数学乃至其他相关学科的认知与爱好.众所周知, 许多数学竞赛题与组合几何有关. 愿中学生、中学老师、大学生及研究生都会从不同角度喜欢这本通俗读物, 各取所需, 各有所得.