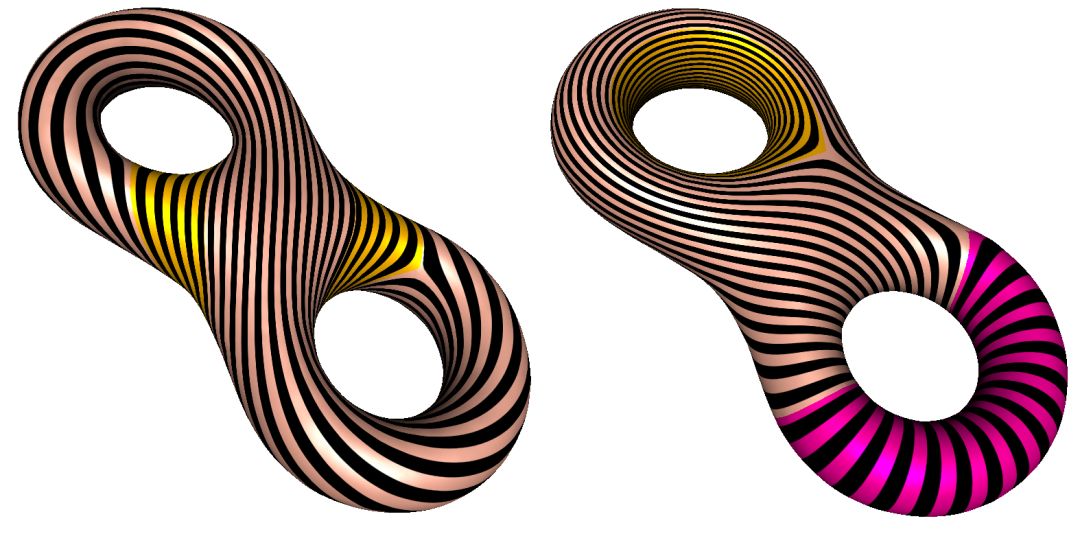行走在纽约的空中

2018 年 5 月 16 日 中国物理学会期刊网 顾险峰

“世界上一半的人生活在纽约，另外一半的人正在赶往纽约的路上。”

纽约是文明的巅峰，也是罪恶的渊薮。无论你是否来过纽约，当你仔细审视自己的文化修养和知识结构，你会惊异地发现太多早已融入你人格的思想源头，都是来自这座不可思议的城市。当你漫步在曼哈顿街头，总会不经意间被眼前的景致和氛围所触动，唤醒久被尘封的记忆：可能是一段缥缈的音乐，一帧模糊的油画，一幕电影的场景，一种不可名状的气味或者一条抽象的数学定理。在你人文知识积累时期，知识结构搭建阶段，纽约的文化已经潜移默化地融入了你的血液。

在老顾的数学知识中，很多定理的创建人都和纽约有着很深的渊源。比如偏微分方程方面的Nirenberg，共形几何和泰希米勒Teichmuller空间理论方面的Gardiner，双曲几何和低维拓扑方面的Sullivan，微分拓扑方面的Milnor，有限元方面的Courant ，当然还有很多知名的数学家。很多时候，老顾在研读他们理论工作的时候，想到他们生活在同一个城市，总是觉得由衷的亲切；欣赏他们精妙绝伦思想，在由衷赞叹的同时总是好奇在曼哈顿的哪个街角能够遇到他们。

结构主义、解构主义

老顾当年学的是布尔巴基学派的结构主义，其根本的哲学思想认为宇宙万物有着基本的数学结构，最为根本的是序结构（时间）、拓扑结构（空间）和代数结构（关系），这些结构相互交织作用，衍生出更为复杂的结构。每种结构有着自身的内在特质，需要特定的语言来描述和专门的理论工具来分析。例如曲面具有拓扑结构，需要用群论的语言来描述和计算；同时具有黎曼度量，需要用到几何偏微分方程来描述和处理；同时曲面也具有共形结构，需要用复变函数理论来描述局部性质，和代数域的语言来描述全局；由高斯-博纳定理，拓扑结构制约着黎曼度量；由单值化定理，共形结构决定了标准黎曼度量；由Hodge理论，拓扑结构决定了曲面上椭圆偏微分方程解空间的维数等等。发现自然界更为深邃而隐秘的结构，揭示基本结构间的内在关系一直是数学家毕生追求的终极目标。

老顾的艺术家朋友们对此却不以为然。他们认为在后现代社会“结构主义”已经过时，“解构主义”正当其时。解构主义对正统原则和标准批判地加以继承，从逻辑上否定传统的基本设计原则，由此产生新的意义。用分解的观念，强调打碎、叠加、重组，创造出支离破碎和不确定感。这两种哲学观念的交锋，在文化艺术领域尤甚。

图1. 图坦塔蒙的黄金面具。

纽约的大都会博物馆可以视为传统结构主义的圣地，各个历史阶段、各种文明的杰作都被珍藏。在这里，老顾有幸曾经亲眼看到过古埃及图坦塔蒙的黄金面具，美轮美奂的古希腊古罗马的雕塑，直至梵高的星空。纽约的现代艺术博物馆成为现代艺术的先锋，解构着传统。例如达利的超现实主义风格的“记忆的永恒”。他受到了弗洛伊德思想的影响，这一思想就是通过自身的潜意识所创作出超真实的景象。作为达达主义的代表人物，达利试图通过废除传统的文化和美学形式发现真正的现实。

图2. 达利的《记忆的永恒》。

在艺术领域之外，解构主义在工程科学和社会经济领域，确有愈演愈烈的倾向。例如在计算机科学中，传统的计算机算法是将人类的知识和洞察转化成程序，用人类的智慧来驱动软件的开发；机器学习的方法是由计算机从数据中自行发掘规律，不再仰仗人类智慧。这一指导思想的转换，彻底解构了计算机科学家的传统思维。恰如现代艺术的发展，使得历史悠久的巴黎画院关闭了绘画专业，机器学习的发展使得世界各地大学的计算机系不再教授“传统智慧”。因为机器学习不需要人类的智慧，人类似乎也不需要传承艰深的知识。阿法狗颠覆了人类关于围棋文化的高雅睿智的看法，也解构了棋手对于棋术棋道的毕生追求。在经济领域，区块链解构了中心金融机构的权威。依随量子计算的实用化，传统的加密机制很快会分崩离析，彻底覆灭。但是在数学领域，似乎解构主义的思潮并没有对数学的进程产生实质性影响，“结构主义”一直大行其道。先贤大师们建立的基本定理一直没有被挑战和颠覆，宇宙间的自然结构亘古永存，自然规律更是独立于人类自行运转。

Highline 风景

图3. 纽约Highline park。

纽约在1930年代修建了一条高架铁路，被称为高线 highline，用于连接肉类加工区和哈德逊港口。历经半个世纪之后被废弃，一度面临拆迁危险。后来高线存活下来，被建成了独具特色的空中花园走廊，成为旧物重建和艺术设计的典范。

highline上依然铺陈着锈迹斑驳的铁轨，枕木间荒草丛生，灌木茂密。间或有几株樱花，繁华轻柔，幽香艳丽，微风袭掠，花瓣如雨。似乎没有游客思古伤情，怀旧叹惋，这和东方的情调截然不同。行走在highline上，俯视桥下的纽约，车水马龙，红尘滚滚。眺望远方，鳞次栉比的高楼拥塞在曼哈顿岛上，空间逼仄，令人窒息。现代社会无情地压榨着每一个人，人类被自身发明的文明所奴役，无处逃遁，难怪解构主义盛行，现代人类怀疑一切的意义。

图4. highline park上的扭曲时空。

高线具有独到的景观，可以眺望到自由女神、帝国大厦、洛克菲勒中心等纽约地标性建筑。同时，沿途可以看到残败破旧的古老厂房，更可以看到奇诡雄伟的现代建筑。古典建筑单调呆板，铅直水平，中规中矩，用经典的欧几里得几何就可以描述。现代建筑对于空间的理解深刻许多，摩天大厦的狂野扭曲，大胆而突兀，在周围的时空中产生了巨大的张力。

图5. highline park上的现代建筑。

建筑表面从方正的矩形变成了光滑弯曲的自由形式曲面，流畅洗练，刚劲而柔和，暮色苍茫中通体透明，墙壁融入了天空，内部灯火通明，璀璨夺目。

图6. Zaha Hadid设计的 Highline Condo.

行走在highline上，不经意间，迎面一幢现代建筑，雍容典雅，柔顺流畅。弧形的落地长窗包络出大厦的轮廓，楼层之间勾勒着优美的曲线。老顾一眼望去，立刻猜到这必是出自国际建筑设计大师扎哈·哈迪德之手，因为这个建筑的最大特色就是曲面的叶状结构（foliation），而叶状结构正是哈迪德的核心品牌。

图6. Zaha Hadid设计的望京Soho.

哈迪德的设计一向以大胆造型出名，被称为建筑界的“解构主义大师”。上图是哈迪德设计的望京Soho中心，更加淋漓尽致地体现出她的设计风格。解构主义建筑在形态上表现为散乱破碎，不遵循古典主义的轴线和秩序，将建筑分解然后再整合。从几何观点而言，哈迪德将曲面分解成柔顺平行的曲线族，这样的曲线族就是曲面的一个叶状结构，每一条封闭曲线被称为是一片叶子，然后再将叶状堆叠成整体形状。

在highline上不期而遇地见到“解构主义大师”的杰作，令老顾陷入深思。解构主义大师用有着严谨数学结构的叶状结构去解构古典建筑设计的理念，突破了建筑传统的桎捁，但却依然遵循着自然的几何结构。

虚拟纤维化猜想

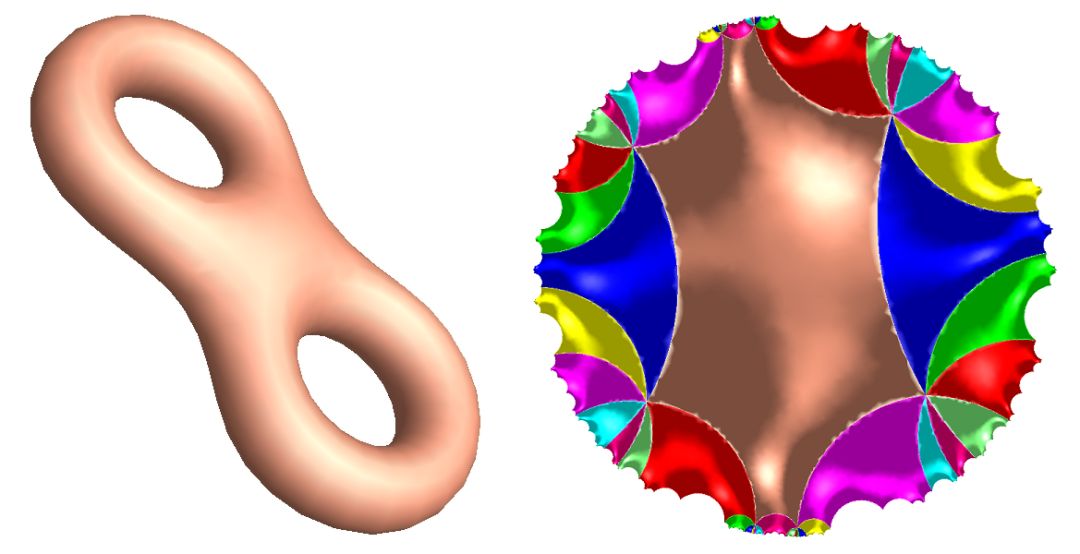
图7. 曲面的双曲度量.

哈迪德为之终生迷恋的叶状结构（foliation）在拓扑和微分几何中起到了至关重要的作用。1980年代，低维拓扑领域发生了天翻地覆的变化，这场革命的领导者Thurston和Sullivan就是应用foliation洞察了三维流形的结构，很多突破就是在highline下的曼哈顿发生。如图7所示，每个高亏格曲面都可以配备双曲度量。固定一个拓扑曲面，其上所有可能的双曲度量构成了Teichmuller空间。

图8. 曲面的叶状结构。

黎曼面上的全纯二次微分构成了线性空间，每个全纯二次微分都诱导了曲面上的一个可测叶状结构，曲面上所有的可测叶状结构也都和某个全纯二次微分诱导的叶状结构等价，（在相差曲面一个和恒通映射同伦的自同胚的意义下）。测度彼此相差一个标量的叶状结构构成一个射影等价类。

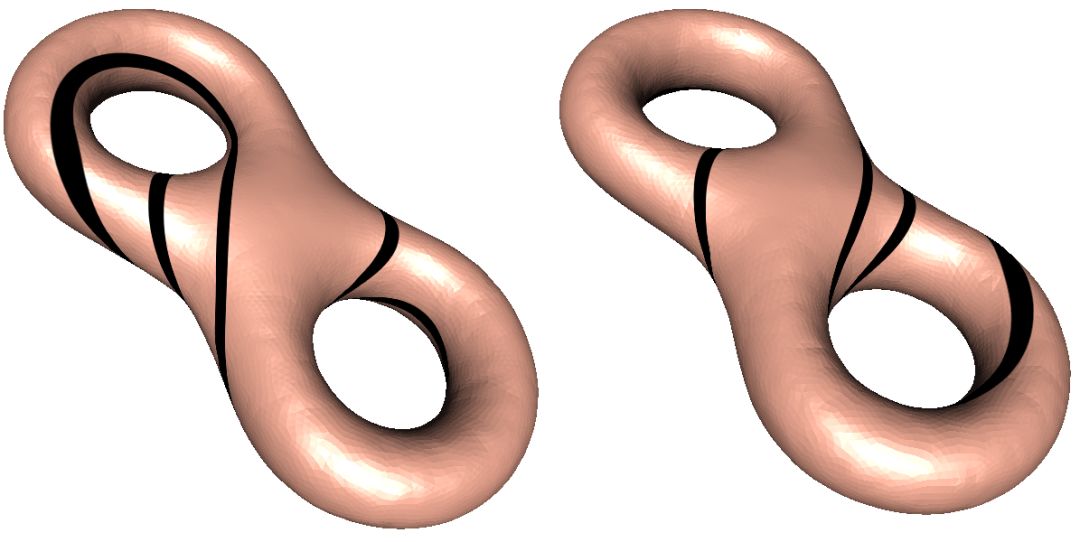
图8. 曲面的简单闭曲线。

可测叶状结构的测度几何意义如下。如图8所示，曲面上的所有简单闭曲线的同伦类构成了曲线空间。曲面上任意一条简单闭曲线会穿越叶状结构的一些叶子（或称纤维），这些叶子的条数定义了叶状结构的测度。可以看出，当我们将简单闭曲线进行同伦变换时，相交叶子的代数条数没有变化，因此一个可测叶状结构定义了曲线空间上的一个函数。

如果给定一个双曲度量，那么每个曲线同伦类中测地线唯一，这些测地线的长度给出了曲线空间上的一个函数。由此，我们看到叶状结构和双曲度量的等价性。

双曲度量构成的Teichmuller空间和等价叶状结构的空间同构；所有的等价叶状结构构成的空间等价于所有全纯二次微分构成的线性空间；由指标定理，Teichmuller空间是一个6g-6维的开球，这里g是曲面的亏格。开球的每根射线是可测叶状结构的射影等价类，这些射影等价类构成了Teichmuller空间的边界，Teichmuller空间并上其边界得到了一个完备的闭球，这一过程被称为是Teichmuller空间的完备化或者紧化。

Thurton考虑曲面到自身的一个自同胚，其拉回度量诱导了完备Teichmuller空间的自映射。根据Brower不动点定理，存在不动点。如果不动点在Teichmuller空间边界，那么有两个叶状结构被自同胚保持，这时曲面映射被称为是Pseudo-Anosov。

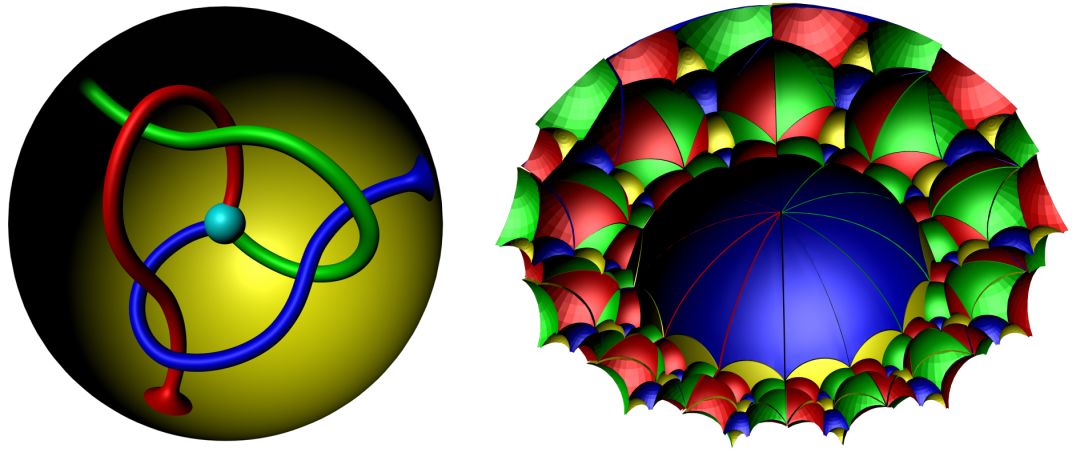
图9. Thurston的苹果。

我们再来考察三维流形。如图9所示，假设三条蛀虫在苹果中打穿了三条彼此缠绕的隧道，如此得到的流形容许一个双曲度量，使得边界表面成为双曲曲面，其覆盖空间在三维双曲空间中的等距嵌入显示在右帧。任意一个三维流形，如果容许双曲度量，被称为是双曲三流形。

Thurston做出了虚拟纤维化的猜想：任意一个封闭双曲三流形，存在一个有限覆盖，同构于一个以圆周为底流形、曲面为纤维的纤维丛，也可以看成是曲面和单位区间的直积，然后将初始曲面和终点曲面用一个Pseudo-Anosov映射粘合。这一猜想目前已经被完美解决。

在highline上，面对扎哈的叶状结构，老顾浮想联翩，从曲面的纤维化直到三维流形的纤维化，从扎哈的解构到低维拓扑的结构。那么，这个虚拟纤维化的结构究竟有什么用呢？

图10. 曲面的四边形剖分。

其实熟悉计算力学的人都知道，将复杂几何实体（三流形）进行结构化规则六面体剖分是非常重要的问题，同时也是极为困难的问题，被称为是这个领域的圣杯。那么，刚才的构造证明了双曲三流形上结构化六面体剖分的存在性。由Pseudo-Anosov映射的不变叶状结构可以构成曲面的四边形剖分，再由纤维丛的局部直积结构将四边形剖分拓展成六面体剖分。如果将这一想法付诸实现，我们需要发明如下算法：双曲三流形的判定；有限覆盖的计算；虚拟纤维化的构造；Pseduo-Anosov不变叶状结构的计算，同时需要解决很多工程方面的问题。老顾希望年轻一代，有人肯花费五六年向这个问题发起冲击。

破坏式创新

行走在纽约的空中，眼前满是扭曲的时空和后现代的艺术，历史和未来交织缠绕，结构主义和解构主义交相辉映，给人以无尽的视觉冲击和思想激荡。AI解构了柯洁的理想，也解构了很多学术范式。在计算机科学领域，现代几何和拓扑尚未大规模渗透，就开始被深度学习解构。区块链正在气势汹汹地解构着传统社会的金融体系，量子计算正在以雷霆万钧之势解构着传统的区块链。非理性主义伴随科技大潮、打着商业模式创新的旗号，将人类裹挟入贪婪癫狂的状态，似乎人类精神文明的一切都要被颠覆。

但是，解构主义的核心是破坏式的结构主义，大自然的结构不会被人类思潮所左右，天荒地老，亘古长存。

请长按下方二维码，选择 “识别图中二维码”，即可关注。