从神话传说到深度学习,谈谈人工智能的60年发展史
编者语:人工智能到现在已经有61年的历史,从它诞生之日起,各种技术难题就随之而来,到底如何创造出一台“会思考的机器”是一直以来科学家们的梦想。从上世纪人工智能初露萌芽,到现在深度学习成为AI的主流技术,科学家们在AI发展不同时期遇到了各种问题,又创造出新的技术来解决问题,本文作者将通过一些实例来简单回顾人工智能技术的发展史。
希腊神话中有这样一个金属巨人:为了保护克里特岛防御海盗和入侵者,人们创造了巨型青铜战士塔罗斯(Talos)。他每天环绕全岛三圈,勇武的造型吓得海盗们只能另觅他处。但在勇猛外表下,塔罗斯并没有所谓的“勇士之心”,他只是个机器人。就像稻草人一样,生来只是为了对外表现出这种骁勇形象。然而信徒们认为,匠人已经为塔罗斯这样的作品灌注了真正的心智、喜怒哀乐、思想,以及智慧。当然这不是真的。塔罗斯也仅仅是梦想的一种外在表现,而这样的梦想几乎贯穿了人类的整个历史:我们多想创造出如同我们自己一样栩栩如生的智慧生命啊。
亦或如作家 Pamela McCorduck 所说:“这就是一种锻造众神的古老愿望”。
科学家、数学家、哲学家,甚至作家,对于创造所谓“会思考的机器”的方法已经思考了很久。同时,又有什么比人类自身更像是“会思考的机器”呢?
自从创造出诸如塔罗斯这样会动的机器后,我们身边的匠人们对于简单的“拟人”智慧就不再感兴趣了,他们开始追求真正的智慧。这些“没头脑”的机器人仅让他们管窥到智慧之表,却并未揭示智慧之本。为此他们必须深入领略智慧最明确的体现:人类的心灵。
正如经济学人所说:“如欲开悟,必先自省(For enlightenment, look within)”。
人们很快意识到,人类与其他不那么智慧的生物间最大的差别,并不在于脑容量或在地球上生存时间的长短,真相其实很简单,仅仅在于我们卓越的推理能力。因此首个可编程计算机的构想产生后,我们会理所当然地认为,这样的计算机将能模拟任何形式的推理过程,至少能够像人一样进行推理。
“计算机(Computer)”这个词的首次使用可以上溯至 1640 年代的英格兰,当时这个词被用于代表“会进行计算的人”。
最开始,创造“会思考的机器”的进展非常缓慢。
1940 年代,当时最先进的哈佛马克一号(Harvard Mark I)是一个重达 10,000 磅,由数千个机械组件驱动的“怪兽”,为了让这个机器动起来,内部共使用了长达 500 英里的线缆。尽管有如此精心巧妙的设计,这个机器每秒钟只能执行三次加法运算。
随着摩尔定律的影响,计算机很快在形式推理各种任务的执行方面获得了超出人类能力的表现。研究人员对所取得的进展感到惊喜,并断言只要按照这样的速度继续发展,首个真正完善的“会思考的机器”变为现实将仅仅是时间问题。
1960 年代,20 世纪知名学者司马贺(Herbert Simon)甚至宣称:“20 年内,机器将能从事人能做到的一切工作”。很可惜,虽然足够惊人,但这个预言没能实现。
计算机确实很擅长解决能够通过一系列逻辑和数学规则定义的问题,但更大的挑战在于让计算机解决无法通过这种以“声明”方式归纳提炼的问题,例如识别图片中的人脸,或者翻译人的语言。
整个世界始终混乱不堪,机器下象棋的水平也许远胜于人类,甚至可能赢得象棋锦标赛冠军,但放眼现实世界,机器的作用其实和橡皮小黄鸭差不多。
(注:小黄鸭调试法,又称橡皮鸭调试法、黄鸭除虫法(Rubber Duck Debugging)是可在软件工程中使用的一种调试代码的方法。方法就是在程序的调试、除错或测试过程中,操作人耐心地向小黄鸭解释每一行程序的作用,以此来激发灵感与发现矛盾。)。
意识到这一点后,很多 AI 领域的研究者开始拒绝承认符号化 AI(Symbolic AI,一种描述形式推理方法的涵盖性术语,至今依然在 AI 研究领域处于支配地位)是创建人工智能机器的最佳方式这一原则。符号化 AI 的基石,例如 Situation Calculus(情景演算)和 First-Order Logic(一阶逻辑)被证明因为过于形式化并且过于严格而无法容纳现实世界中的所有不确定性。我们需要新的方法。
一些研究人员决定通过更为巧妙的“模糊逻辑(Fuzzy Logic)”寻求答案,在这种逻辑范式中,真实的值不是简单的 0 和 1,而可以是介于这两个数之间的任何值。还有其他研究人员决定专注于别的新兴领域,例如“机器学习”。
机器学习弥补了形式逻辑的不足,可顺利解决真实世界的不确定性问题。这种方式并不需要将有关现实世界的所有知识“硬编码”至一系列严格的逻辑公式中,而是可以教计算机自行推导出所需知识。
也就是说,我们并不需要告诉计算机“这是一把椅子”或“这是一张桌子”,我们可以教计算机学习如何将椅子和桌子的概念区分开来。机器学习领域的研究人员会谨慎地避免使用确定性概念描述整个世界,因为这种严格的描述特性与现实世界的本质是截然相悖的。
于是他们决定使用统计学和概率论语言来描述整个世界。
机器学习算法并不需要了解真理和谬误,只需要了解真实和虚假的程度,也就是概率。
这种使用概率,以数值方式了解现实世界中所存在不确定性的想法,使得贝氏统计学(Bayesian statistics)成为机器学习的基石。“频率学派(Frequentists)”对此有不同看法,不过这个分歧还是另行撰文介绍吧。
很快,诸如逻辑回归和朴素贝叶斯等简单的机器学习算法已经可以教计算机区分合法邮件和垃圾邮件,并能根据面积预测房屋价格。逻辑回归是一种相当简单的算法:给出一个输入向量 x,模型会直接将这个 x 分类至{1, 2, …, k}多个类别之一。
然而这就会导致一个问题:这种简单算法的效果严重依赖所使用的数据表达方法。
为了更形象地理解这个问题,可以试着假设构建一种使用逻辑回归判断是否建议进行剖腹产的机器学习系统。系统无法直接检查产妇,因此需要通过医生提供的信息来判断。这种信息可能包含是否存在子宫疤痕、怀孕月数、产妇年龄等。每个信息可以算作一个特征,通过将不同特征结合起来,AI 系统就可以全面了解产妇的表征。
通过提供训练数据,逻辑回归算法可以学习产妇的不同特征与各种结果之间的关系。例如,算法可以从训练数据中发现,随着产妇年龄的增长,分娩过程中出现“恶心反胃”情况的风险会增加,因此算法会降低向高龄产妇推荐自然分娩的概率。
虽然逻辑回归可将表征与结果对应,但实际上并不能决定哪些特征可以组成产妇的表征。
如果直接为逻辑回归算法提供患者的 MRI (核磁共振)扫描结果,而非医生的正式报告,那么算法将无法提供有用的预测。
单纯就 MRI 扫描结果中的每个像素来说,几乎无法帮助我们判断产妇分娩过程中遇到并发症的可能。
足够好的表征,与足够好结果之间的依赖性广泛存在于计算机科学和我们的日常生活中。例如,我们几乎可以瞬间在 Spotify 上找到任何歌曲,因为他们的曲库很可能就是用智能的数据结构来存储的,比如说会是三元搜索尝试(Ternary search tries),而非常见的简单结构,例如无序数组。另一个例子:学童可以使用阿拉伯数字轻松进行数学计算,但如果使用罗马数字,情况就截然不同了。机器学习也是如此,输入表征的选择将对学习算法的效果产生巨大影响。
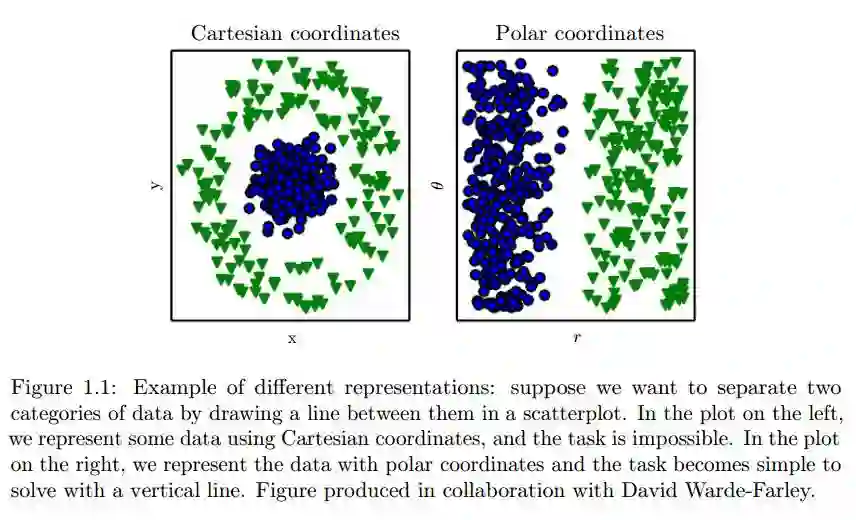
图 1.1:不同表征的范例:假设我们需要在散点图上画一根线将两类数据分开。左图使用笛卡尔坐标系呈现这些数据,此时几乎无法做到;右图对同一批数据使用了极坐标系,一条竖线即可解决问题。此图与 David Warde-Farley 合作制作。 David Warde-Farley, Goodfellow et al. 2017
因此人工智能领域的很多问题实际上可以通过为输入数据寻找更适合的表征这种方式进行简化。假设我们要设计一套算法来学习识别 Instagram 照片中的汉堡。首先要构建一个用来描述所有汉堡的特征集。最初我们可能会用图片中的原始像素值来描述汉堡,一开始你也许觉得这种做法很合理,但很快会发现根本不是这样。
单凭原始像素值,很难描述汉堡看起来是什么样的。想想你自己在麦当劳点汉堡时的场景吧:你也许会用不同“特征”来描述自己想要怎样的汉堡,例如奶酪、三分熟的牛肉饼、表面撒有芝麻的圆面包、生菜、红洋葱,以及各种酱料。结合这种情况考虑,也许可以用类似的方式构造我们需要的特征集。我们可以将汉堡描述成一种不同成分的集合,每个成分又可以用各自不同的特征集来描述。大部分汉堡的成分都可以用其颜色和外形来描述,进而汉堡作为整体也就可以使用不同成分的颜色和外形来描述了。
但如果汉堡不在照片正中央,周围有其他颜色相近的物体,或者是一间风格迥异的餐厅,他们提供没有“组装”在一起的汉堡,此时又该怎么办?算法该如何区分这些颜色或几何造型?最显而易见的解决方式无疑是增加更多(可分辨的)特征,但这也仅仅是权宜之计,很快你将会遇到更多边缘案例,需要增加更多特征才能区分类似图片。
输入的表征越来越复杂,计算成本增加,同时会让情况变得更棘手。因此从业者现在不仅需要关注数量,同时也要关注所输入表征中,所有特征的表现能力。对于任何机器学习算法,寻找完美的特征集都是一个复杂过程,需要花费大量时间精力,甚至需要大量有经验的研究人员投入数十年的时间。
确定如何以最佳方式呈现输入给学习算法的数据,行话来说实际上是一种“表征”问题。
1990 年代末到 2000 年代初,机器学习算法在不完美输入表征方面的局限对 AI 发展产生了巨大阻碍。在设计输入特征的表征时,工程师们没有任何选择,只能依赖人类自身的才智以及围绕问题所在领域的先验知识(Prior knowledge)克服这些局限。长久以来,这样的“特征工程”始终站不住脚,如果某个学习算法无法从未筛选的原始输入数据中提取出任何见解,那么用更具哲学意义的话来说,它就无法理解我们的世界。
面对这些困难,研究人员快速发现了一种应对之道。如果机器学习算法的目标是学着将表征与输出结果进行映射,为何不教它们学习表征本身。这种方式也叫做表征学习。最著名的例子可能就是 autoencoder,这是一种神经网络,根据人脑和神经系统进行建模的计算机系统。
Autoencoder 实际上是编码器(Encoder)函数和解码器(Decoder)函数的组合,编码器函数负责将输入的数据转换为不同表征,解码器函数负责将中间态的表征重新转换为原始格式,并在这一过程中尽可能多地保留信息。这样就可以在编码器和解码器之间产生一个分界(Split),输入的“噪音”图像可解码出更有用的表征。例如,噪音图像可能是一张 Instagram 照片,其中有一个汉堡,周围还有很多颜色近似的物体。解码器可以消除这些“噪音”,只保留描述汉堡本身所需的图片特征。
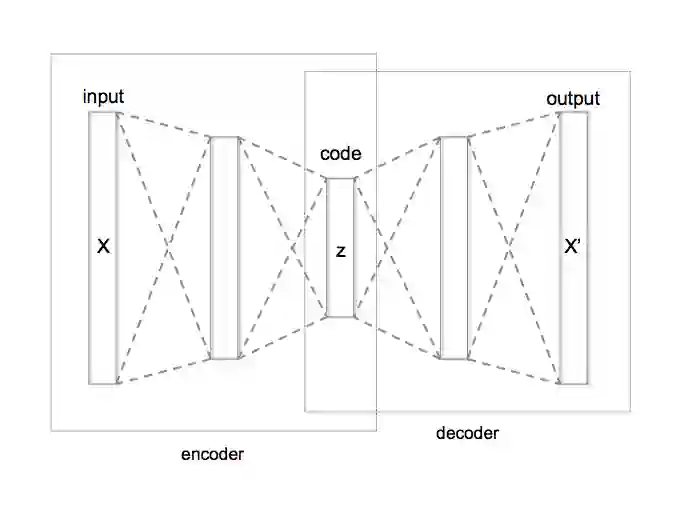
作者:Chervinskii,自行制作,依 CC BY-SA 4.0 方式许可:https://commons.wikimedia.org/w/index.php?curid=45555552
但就算有了 autoencoder,问题依然存在。为了消除噪音,autoencoder(以及任何其他表征学习算法)必须能精确确定哪些因素对输入数据的描述是最重要的。我们希望自己的算法能选择恰当的因素,使其更好地识别出真正感兴趣的图片(例如包含汉堡的图片),并排除不感兴趣的图片。
在汉堡这个例子中,我们已经明确,如果能更专注于图片中不同元素的外形和颜色,而非只关注图片的原始像素值,就可以很好地区分包含和不包含汉堡的图片。然而永远都是知易行难。重点在于教算法如何从不重要的因素中解读出重要的因素,也就是说,需要教算法识别所谓的因素变体(Factors of variation)。
初看起来,表征学习似乎没法解决这个问题,别着急,再往后看看。
编码器接受输入的表征并通过传入一个隐藏层(中间层),将输入结果压缩为略小一点的格式。解码器的作用截然相反:将输入内容重新解压缩为原始格式,并尽可能多地保留信息。两种情况下,如果隐藏层能够知道哪些因素是描述输入内容时最重要的,并尽可能确保这些因素在该层传递过程中不会从输入数据中消除,输入数据中包含的信息将得到最大程度的保留。
在上图示例中,编码器和解码器分别只包含一个隐藏层:一层用于压缩,一层用于解压缩。这种粗粒度的层数意味着算法在判断如何以最佳方式对输入数据进行压缩和解压缩,进而保留最大量信息的过程中缺乏足够灵活性。但如果略微改动一下设计,引入多个隐藏层并按顺序堆叠在一起,在选择重要因素时,算法就可以更自由地判断对输入数据压缩和解压缩的最佳方式。
这种在神经网络中使用多个隐藏层的方法就是深度学习。
深度学习还可以更进一步。在使用多个隐藏层后,只需构造一个更简单的层就可以建立复杂的表征。通过按顺序堆叠隐藏层,我们可以在每一层中识别新的因素变体,这样算法就可以用更简单的层表达更复杂的概念。
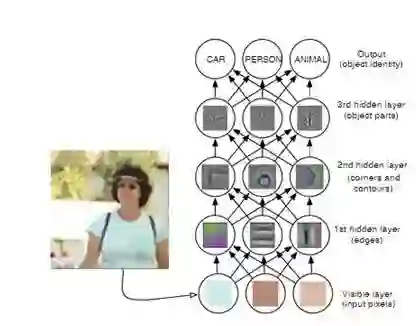
Zeiler and Fergus (2014)
深度学习有着深远悠久的历史。
这一领域的中心思想早在 1960 年代就已通过多层感知器(Multi-layer perceptrons)的形式诞生,后来在 1970 年代首次出现了更实用的反向传播算法,1980 年代出现了人工神经网络。尽管历史悠久,这些技术依然花了数十年才变得实用。这些算法本身并不差(尽管很多人这样想),我们只是没有意识到为了让他们变得足够实用需要提供多大量的数据。
由于统计噪声的影响,小规模数据样本更有可能获得极端的结果。然而只要增大数据量,就可以降低噪声影响让深度学习模型更精确地确定输入数据最适合的描述因素。
21 世纪初,深度学习终于一飞冲天,很多大型科技公司发现自己正坐在数据金矿顶端,大把的数据资源等待被开发。
本文最初发布于原作者 Mark Aduol 的博客,经原作者授权由 InfoQ 中文站翻译并分享。
关注 AI 前线公众账号(直接识别下图二维码),点击自动回复中的链接,按照提示进行就可以啦!还可以在公众号主页点击下方菜单“加入社群”获得入群方法~AI 前线,期待你的加入!