基于PCA降维和BP神经网络的人脸识别（文末附完整数据和代码）

会员服务 ·

基于PCA降维和BP神经网络的人脸识别（文末附完整数据和代码）

2018 年 4 月 26 日 全球人工智能 马一十二

高薪招聘兼职AI讲师和AI助教！

1.ORL人脸库

ORL人脸库诞生于英国剑桥Olivetti实验室。

ORL人脸数据库共有40个不同年龄、不同性别和不同种族的对象。每个人10幅图像共计400幅灰度图像组成，图像尺寸是92×112，图像背景为黑色。其中人脸部分表情和细节均有变化，例如笑与不笑、眼睛睁着或闭着，戴或不戴眼镜等。

取每个人前5幅图像，共计200幅用来训练，其余用于测试。

2.PCA（主成分分析法）

Step 01：样本中心化和标准化

Step 02：求其协方差矩阵

Step 03：求协方差矩阵的特征值和特征向量

Step 04：选择k个最大特征值，然后将对应的特征向量分别作为列向量组成特征向量矩阵

Step 05：将样本点投影到选取的特征向量上，投影后的数据FinalData为：

FinalData(m∗k)=DataAdjust(m∗n)×EigrnVectors(n∗k)

其中DataAdjust(m∗n)是中性化后的样本矩阵，EigrnVectors(n∗k)是选择的k个最大特征值所对应的特征向量所构成的特征向量矩阵。

对数据进行中心化预处理，这样做的目的是要增加基向量的正交性，便于高维度向低纬度的投影，即便于更好的描述数据。

（图片来自知乎：https://www.zhihu.com/question/37069477)。

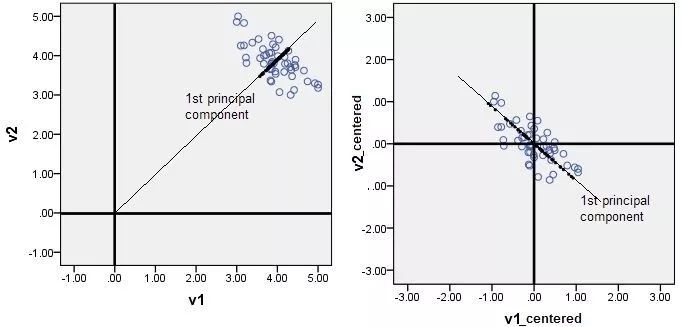
对数据标准化的目的是消除特征之间的差异性，当原始数据不同维度上的特征的尺度不一致时，需要标准化步骤对数据进行预处理，使得在训练神经网络的过程中，能够加速权重参数的收敛。

过中心化和标准化，最后得到均值为0，标准差为1的服从标准正态分布的数据！！！

求协方差矩阵的目的是为了计算各维度之间的相关性，而协方差矩阵的特征值大小就反映了变换后在特征向量方向上变换的幅度，幅度越大，说明这个方向上的元素差异也越大（越有投影的必要，矩阵相乘的过程就是投影），故而选取合适的前k个能以及小的损失来大量的减少元数据的维度。

function [pcaA V] = fastPCA( A, k )
% 快速PCA
% 输入：A --- 样本矩阵，每行为一个样本
%      k --- 降维至 k 维
% 输出：pcaA --- 降维后的 k 维样本特征向量组成的矩阵，每行一个样本，列数 k 为降维后的样本特征维数
%      V --- 主成分向量
[r c] = size(A);
% 样本均值
meanVec = mean(A);
% 计算协方差矩阵的转置 covMatT
Z = (A-repmat(meanVec, r, 1));
covMatT = Z * Z';
% 计算 covMatT 的前 k 个本征值和本征向量
[V D] = eigs(covMatT, k);
% 得到协方差矩阵 (covMatT)' 的本征向量
V = Z' * V;
% 本征向量归一化为单位本征向量
for i=1:k
    V(:,i)=V(:,i)/norm(V(:,i));
end
% 线性变换（投影）降维至 k 维
pcaA = Z * V;
% 保存变换矩阵 V 和变换原点 meanVec
save('Mat/PCA.mat', 'V', 'meanVec');

MATLAB自带的那个确实是有点慢了，用的是Fast_PCA，最后选取了49维特征作为输入。

3.BP神经网络的概念

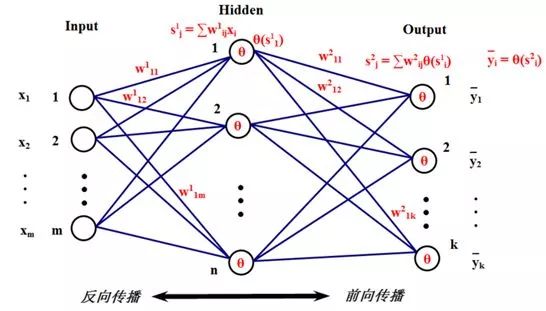
BP神经网络是一种多层的前馈神经网络，其主要的特点是：信号是前向传播的，而误差是反向传播的，依次调节隐含层到输出层的权重和偏置，输入层到隐含层的权重和偏置。

%创建并训练BP神经网络

%生成训练BP神经网络的输入 P 
P=TrainData;
%生成目标输出矢量 T
T=zeros(200,40);
 for i=1:40
    for j=1:5
      T((i-1)*5+j,i)=1;
  end
 end
%打乱训练样本顺序
gx2(:,1:k)=P;
gx2(:,(k+1):(k+40))=T;
xd=gx2(randperm(numel(gx2)/(k+40)),:);
gx=xd(:,1:k);d=xd(:,(k+1):(k+40));
P=gx';
T=d';
%创建BP神经网络
[R,Q]=size(P);
[S2,Q]=size(T);
net=newff(minmax(P),T,[fix(sqrt(R*S2))],{'purelin','purelin'},'traingdx');
%训练BP神经网络
net.trainparam.epochs=5000;    %训练步数
net.trainparam.goal=0.0001;    %训练目标误差
net.divideFcn = '';            %所有的样本都用于训练
[net,tr]=train(net,P,T);       
%仿真BP神经网络
Y=sim(net,P);

参数：输入层49，输出层40

输入层到隐含层传递函数：'purelin'。

隐含层到输出层传递函数：'purelin'。

训练函数：'traingdx'（动量及自适应lrBP的梯度训练递减函数）。

最后的识别准确率并不是很理想

仅为89.5%-90.5%

原文链接：https://zhuanlan.zhihu.com/p/35943230

作者：马一十二

数据和代码：https://link.zhihu.com/?target=https%3A//pan.baidu.com/s/1qFCocFsKfJT-9aUIbQvT7A

密码：66e4

- 加入人工智能学院系统学习 -