双节赠书 |《数学也荒唐》- 早餐代表我的心

会员服务 ·

双节赠书 |《数学也荒唐》- 早餐代表我的心

2017 年 9 月 30 日 遇见数学 杰罗姆.科唐索

国

庆

有

礼

普

天

同

庆

10月1日赠书

《数学也荒唐》

数

学

也荒唐

早

餐

代表我的心

请输入标题 abcdefg

“亲爱的，天亮了，今天是 2 月 14 号，我特意为你准备了早餐。不用起床了，就在床上吃。好丰盛的，有刚出炉还冒着热气的羊角面包，有一大杯我刚刚亲手榨的橙汁，有新鲜水果，还有最重要的，一大碗牛奶！”

“你对我太好了，但为什么有牛奶呢？你知道我喝牛奶不消化啊……”

“很简单啊，因为这碗牛奶代表我对你的爱，你看看碗里面有什么……”

图 1.1　阳光照射下的碗里出现心形（图片来源：© Gérard Janot, CC BY-SA 3.0）

早餐是一天中最重要的一餐。每天早上，我都目光呆滞地盯着麦片盒上的配料表，心里默念这句话，等着没睡够的倦意退去。如果你泡了碗麦片，冲了杯咖啡或者倒了杯果汁，那么，在阳光的照耀下，杯子里面会出现一个类似心形的形状（图 1.1）。

这个心形是怎么来的呢？

答案其实很简单，但先要了解下数学家是如何定义心形的。

刚好遇到你，

刚好爱上你，

刚好在一起，

刚好幸福了。

【画一颗心给你！】

画法是这样开始的

有了合适的方程和绘图仪，什么东西都可以画出来。Wolfram 公司市场部的编辑理查德·克拉克特别擅于用傅里叶变换写图形方程。有了他的贡献，我们才能把皮卡丘也用方程表示出来（图 1.2a）——我在这里就不把方程写全了，如果要写全，一页纸都不够。美国一所高中的数学老师 J. 马修 · 雷吉斯特也是图形方程的好手。2011 年，他的学生把他的蝙蝠侠图标方程（图 1.2b）发到了网上，引起了轰动。言归正传，数学爱好者给出了许多心形方程，各有千秋，但数学界“心有独钟”：他们认定用简单方程描绘的“心形线”（图 1.2c 和图 1.2d）。

(a) 理查德·克拉克的皮卡丘曲线。这是一个参数方程，t的取值在0到2π之间，曲线上某一点的坐标由(x, y)关于t的函数确定，即(x(t), y(t))。这里只给出了皮卡丘轮廓线的方程，完整的方程是其10倍长。

(b) J.马修·雷吉斯特的蝙蝠侠图标曲线。起初方程只有一个解析式，以椭圆方程和直线方程为基础

心形线在英语里叫作 cardioid，这个词来自希腊语：kardia 意为“心”，eidos 意为“形”。心形线有许多不同的定义方法，但是异曲同工（图 1.2）。我们可以想象一个圆沿着另一个圆外侧滚动而不滑动，不动的圆叫作“准圆”，动圆上某一点的轨迹称为“外摆线”（epicycloid），这个词也来自希腊语：epi 意为“上”，kuklos 意为“圆”。准圆和动圆的半径相等时，就得到了心形线。如果动圆在准圆内部，而准圆的半径是动圆的 2 倍，也会得到心形线。

18 世纪初，布莱兹·帕斯卡的父亲艾蒂安·帕斯卡在对摆线的研究中提到了这种曲线，虽然言辞含糊，但这是历史上首次出现。其他数学家对这种曲线也是兴致勃勃。1708 年，法国数学家菲利普·德拉意尔证明心形线的长是准圆半径的 16 倍。直到 1741 年，乔瓦尼·达卡斯蒂利奥内才根据形状将其命名为“心形线”。

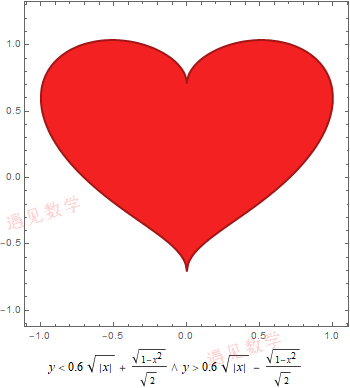
(c)

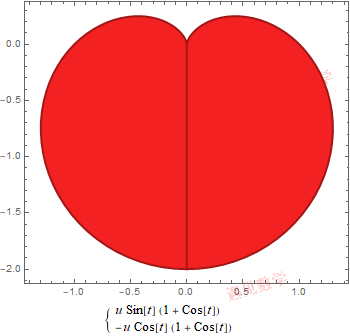
(d)

图 1.2　几条有趣的曲线

(c, d 两图由 [遇见数学] 重新绘制)

第二种构建心形线的方法是：取圆上一点 P，以圆上其他点为圆心，作经过点 P 的圆，所有这些圆内包于一条心形线。

更让人意想不到的是，心形线还可以通过数论的方法来构建。在圆周上均匀地取 100 个点，编为 0 到 99 号，然后把各个点与编号为其 2 倍的点相连，如果编号的 2 倍大于等于 100，则以减去 100 计，即编号乘 2 得 100 则对应点 0，编号乘 2 得 102 则对应点 2。按这种方法，点 21 与点 42 相连，点 53 与点 6 相连。所有这些线段形成心形线。取的点越多，心形线就越准确（见下面几个图）。

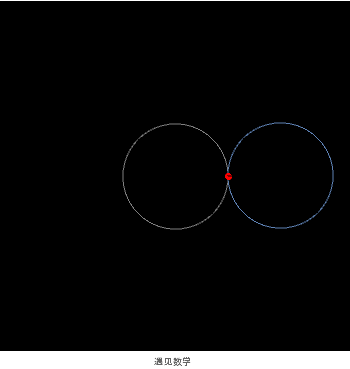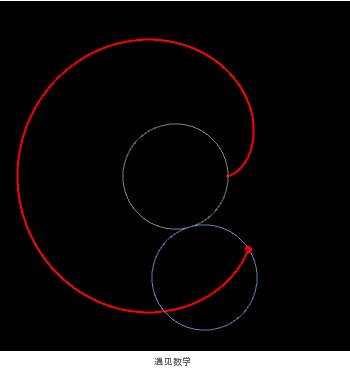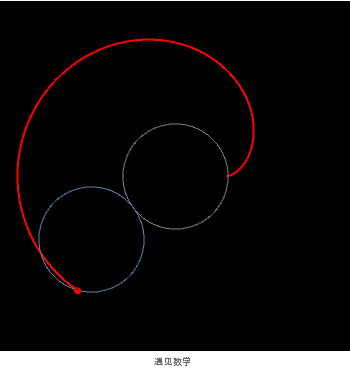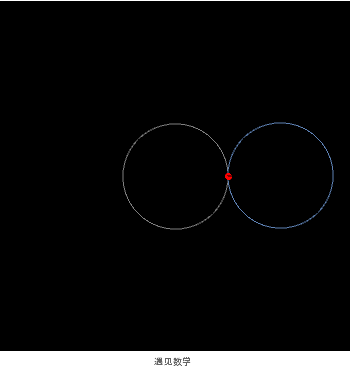
可以是圆的外摆线

也可以是经过圆周上一点且圆心也在此圆周上的圆的包络线

或者圆周上某点与其 2 倍编号点连线的包络线

说了这么多，还没有解释碗里怎么会有一颗“心”。真正原因是，心形线是圆的“散焦线”。

请输入标题 abcdefg

【光之几何】

光线照射到圆形容器的边缘，会发生反射。假设阳光是平行光，让我们来观察一下反射光路：根据光的反射定律，反射角等于入射角，即反射光线与法线的夹角等于入射光线与法线的夹角，法线是圆在入射点上切线的垂线（图 1.4）。

图 1.4　光在曲线上的反射

根据光的反射定律（又称“斯内尔 - 笛卡儿第一定律”），反射角（红色）等于入射角（蓝色）。

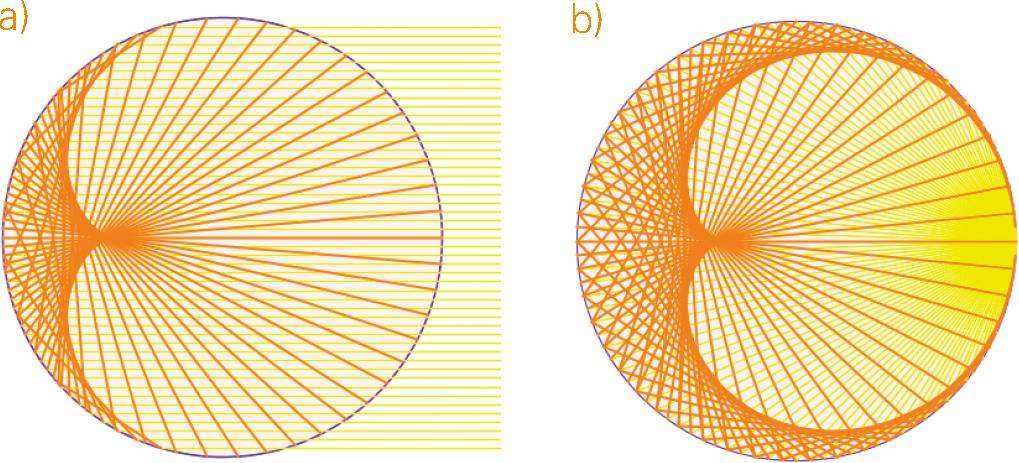
图 1.5　(a) 将阳光视为平行光，反射以后形成的“散焦线”与心形线很相似。这其实是另一种外摆线，称为“肾形线”。(b) 当光源位于圆周上的一点时，才能得到心形线

阳光视为平行光，照射到杯沿并经过反射后，汇集成的曲线就是所谓的“散焦线”，与所有反射光路相切。这里的散焦线和心形线很相似（图 1.5a）。

但是，这样得到的曲线并不是真正的心形线，心形线与圆周不会相交。其实，这是半肾形线，可以视为心形线的“亲戚”，因为它们都是外摆线的一种。如果准圆的直径是动圆的 2 倍，就会得到肾形线（图 1.6）。肾形线有两个对称轴和两个回复点，即曲线好像要往回走的那一点。“肾形线”这个词英语为 nephroid，也来自希腊语，nephrós 意为“肾”。这听起来就没“心形线”那么浪漫了。

图 1.6 如果准圆的半径是动圆的 2 倍，则动圆上某点的轨迹是另一种外摆线，称为“肾形线”

但不要担心，想要杯子里出现心形线很简单，只要把光源移近一点就行。光源在杯子的圆周上时，出现的就是标准的心行线（图 1.5b）。下一个情人节，你就可以省着点过啦！不用去高级餐厅吃大餐，只要一盏灯和一碗牛奶就够了，然后再给他或她念一首诗，完美！

不过如果你真的这么做了，但你的心上人并不领情，作者不承担任何责任。

请输入标题 abcdefg

如果你是外摆线，你会是一条心形线。

如果你是全纯函数，你就是正弦的平方，

而我就是余弦的平方，我们刚好合二为一。

如果你是偶数，你会是 28，因为 28 是完全数。

如果你是奇数，你依然会是完全数。

但只有我知道，你这个奇完全数的存在。

如果你是对数，你将会……那个……你懂的。

请输入标题 abcdefg

10.1 赠书活动

《数学也荒唐》

编者著：杰罗姆.科唐索

译著者：王烈

出版社：人民邮电出版社

出版年：2017年8月

该书用20个数学问题，探讨了代数、概率学、统计学、平面几何、图论、拓扑学等主题，分析角度十分独特，语言幽默风趣，内容充实，贴近生活，在意想不到的趣题中探讨数学知识. 本文选自第一章, 已获许可发布此章节, 特此感谢图灵支持!

本次 [遇见数学] 联合 [图灵教育] 送出 3 本《数学也荒唐：20个脑洞大开的数学趣题》, 你遇到过那些与数学相关有趣的人或事呢? 小编会从精选后评论中, 选点赞最多的前三位赠书, 截止日期 10.8 日 23:59 分截止. 等不及的朋友可以通过文末 [阅读原文] 购买原书或移步图灵社区选择电子版.

明日赠书活动: 《用数学的语言看世界》