优化算法从鸟群、鱼群中借鉴了啥 | 腾研识者

“算法科普”系列之二

生活工作中，很多时候都是在寻求最优解。

比如选择进入哪个行业去工作，怎样填写高考志愿，怎样找到自己深爱的伴侣，怎样在合适时机和地点购房，怎样在变幻莫测的股市中淘金，怎样在平衡客户需求和开发能力之间找到一个成本-效益最佳的项目方案，等等。

这些待解决的问题，按理说，都有最优解。

而本期腾研识者岳亚丁博士将告诉你，算法是如何借鉴大自然中的鸟群、鱼群等，来找寻最优解的，以及算法是不是可能自己设计算法。

文章要点：

• 哪些问题需要优化算法？
  

• 设计优化算法时，大自然给了我们什么启发

• 举个例子看优化算法到底啥样

• 摆脱对大自然的依赖，自创更好的优化算法

算法工程师与他的好友在公园观鱼。一群色彩斑斓的锦鲤在水面翻腾，追逐着游人们抛下的鱼食。

最优决策需要优化算法

：想什么呢？你不想喂它们吗？

：我在想，这些鱼游动的轨迹，与鱼群算法有多么的相似。

：这里也有算法？

：你看，它们时而捕食，时而群聚，时而追随，时而漫游，最终目的是尽快找到更多的食物，同时又避免可能的风险。鱼群算法，正是由此而来啊。

：你说的鱼群算法，是指仿生学吗？

：不是。仿生学主要是借鉴生物界的形态、结构、功能，设计出新的机械、装置、设备，比如人类受鱼类形状的启发，设计出水下航行的潜艇；或者通过研究鸟类肢体构造和飞行技能，来改进飞机的性能。

鱼群算法，则是受鱼群行为的启发，设计出的一种算法，可以用来找到问题的最优解。

：问题的最优解，是什么意思？

：我们生活和工作中，很多时候都是在寻求最优解。

比如说，选择进入哪个行业去工作，怎样填写高考志愿，怎样找到自己深爱的伴侣，怎样在合适时机和地点购房，怎样在变幻莫测的股市中淘金，怎样在平衡客户需求和开发能力之间找到一个成本-效益最佳的项目方案，等等。这些待解决的问题，按理说，都有最优解。

：听起来，像是在做最优决策。

：是同一个意思。人是智慧生物，是解决问题的高手，有分析、综合、归纳、推理等能力，有寻找最优解的能力。

但是当面临的问题规模太大，复杂程度太高，特别是大社会、大工业中的问题，要找到最优解，哪怕记忆力再好、再聪明的人脑也吃不消了，靠直觉、拍脑袋做决策，已经不靠谱，还是需要用计算机来帮忙做这个事情，这时就需要优化算法了。

：计算机算数还是挺快的，听说都每秒多少亿次了，用它做优化，还没怎么听说。所以你让它模仿鱼群？

：计算机比较笨，只能按照我们人类的指令来做事情，但它最大的特点是算得快，我们可以利用这个特点来做更复杂的事情，包括优化。

勤能补拙嘛。我先通过一个简单例子，解释一下计算机是怎么做优化的，然后再说鱼群的事。

：好吧，你说说看。

一种简单的优化算法

：假设有一个人，在漆黑不见五指的夜里，独自登山，目标是山顶，你觉得他应该怎么做？

：山上不会有断崖、溪流、野兽吧？

：暂时假定没有这些危险东西。

：那就只能四处伸脚试试，感受一下，哪个方向是向上的，就往那个方向走呗。

：是的。这也正是计算机的最简单的优化算法之一。山顶就是待求的最优解。

从某个坐标点（东经多少度、北纬多少度）出发，算法开始之后，给计算机一个旁边紧挨着的新坐标点（相当于人往某个方向挪动一步），它算一下，是不是好些（人感觉是不是升高了一点），如果是，计算机就认定这个坐标点更好（人就往这个方向走一步），然后在这个点的基础上继续尝试；否则，就退回来，给它旁边另一个坐标点算一下（人往另一个方向挪动一步），再试。

就这样逐步尝试，走了很多步之后（所幸计算机“走”得挺快），如果发现四处挪动都是下降的方向，就算是到达山顶了。

：是够笨的，但是听起来，似乎还是有效的。

：对呀。

：不过，我觉得这里有一个问题。按照这样的方案，会不会走到了一个小山包的顶端，甚至一个小土堆上，就以为到山顶了，而实际上真正的山顶还远着呢？

：你说得对。小山包的顶端，只是一个局部的最优解，真正的山顶，才是一个全局的最优解。我们当然希望找到后者。上面说的算法还不是一个非常好的算法，它有可能找不到全局最优解。

：还有一个问题：如果能够通过鞋底感觉到地面的不平，有点倾斜，那就不需要前后左右地伸腿尝试，而只要按照鞋底感觉到的往上倾斜的方向走，这样岂不是更快？

：正是！如果待求问题与目标之间可以表示为一个数学公式，我们一般就可以求出哪个方向是往上倾斜的，然后让计算机沿着那个方向进行搜索，就更快捷了。

学术界把这种算法叫做“瞎子爬山法”。但是很多情况下，待求问题很复杂，没法写出一个数学式子，所以还是得四处伸脚尝试。

：这也是没有办法的办法了。

：但这样也好，可以处理更多类型的问题。

例如，学生成绩受很多因素影响，包括学生的年龄、性别、学习时长、健康程度、家庭背景等等，但到底是怎样影响的，我们可能写不出一个很精确的数学公式来（总不能瞎编一个“数学期考成绩 = 年龄x平均每天学习小时数”吧）。

也没必要去写，可以通过“伸腿”去试，照样可以求得最优解，从而得知怎样才能获得更高分数。

：最后一个问题：如果真的有断崖、溪流这些东西，怎么办？

：现实世界中，它们当然对爬山人构成阻碍和威胁。计算机做的话，都是在虚拟世界中尝试，即使突然发现“踩空一脚”，也没什么大不了的，照样可以退回来，不影响后续的逐步搜索。

：这个瞎子爬山法，除了用来爬到山顶，还能用于更复杂的问题吗？比如说炒股，你前面也提到了的。

：瞎子爬山法难以胜任，其它优化算法恐怕也够呛，因为股市数据的随机性太强。当然，也可以试一试，只要能够把问题用数值表示出来。

炒股的情况虽然很复杂，但简略地讲，我们的目标，还是希望一段时间内的投资收益最大化；要寻找的，则是应该买哪几只股票，买多少股，持有多长时间，等等，这些待求的东西，都是可以表示成一组数值的，就跟上面爬山的情况那样，那里是用经纬度坐标值来表示的。

：你是说，把待求的东西表示为一组数（如经纬度、股票仓位），目标是另一个数（如海拔、收益），然后让优化算法来找出能使目标最大的一组数，对吗？

：是的，这就是优化算法的本质。

鸟群算法的优势

：比瞎子爬山法好的优化算法，有哪些？

：还有鱼群、鸟群、蜂群、蚁群、萤火虫、细菌、猴群、布谷鸟、蝙蝠、病毒、免疫系统、生物进化 …… 

人们从它们的行为得到启发，设计了优化算法，很多情况下，它们比瞎子爬山法好。

：嚯！开动物园了。

：也有非生物的，例如，和声、水滴、螺旋、星系、重力、量子……

：够多的了。能举一个例子吗？我来感受一下比瞎子爬山法好在哪里。

：就说说鸟群算法吧，它比起鱼群算法更简单一点，也相对容易解释一点。

：好。

：鸟群算法里面，假设食物就像蚊虫，不均匀散落在空中，在某些点更密集。一群鸟在空中盘旋飞翔，想找到那个食物最集中的点，也就是全局最优点。

：有一只头鸟带领它们飞吗？

：不需要，假定每只鸟的能力都一样。每只鸟的下一步飞翔方向受到三股力量的影响：第一，是当前的飞翔方向，即它自身有一定惯性，会有一股力量想拉着它沿着当前的方向飞。

第二，是它自己迄今为止经过的食物最密集的某个点，它对此还有记忆，觉得那个点有戏，于是也会受到那个点的牵引，尽管那个点不一定是全局最优点。

第三，假设鸟群之间是有通信联系的，随时保持沟通，对于整个鸟群迄今为止经过的食物最密集的某个点，每只鸟都是知道的，于是这只鸟也有点受那个点的牵引，尽管那个点也不一定是全局最优点。

：这样的假设，好像还是有道理的，但不知道是否符合实际情况。

：对实际情况，我们可能无法准确知道。但是设计一种算法，只要借鉴生物的一部分行为，只要效果好，也就可以了，不一定非要完全符合实际情况。

：然后呢，鸟群怎么飞？

：每只鸟受三股力量的牵引，在空中飞翔，会逐渐向最优点靠拢。

飞了一段时间后，估计差不多了，就盘点一下，所有鸟截止到最后时刻经过的食物最密集的某个点，就被认为是全局最优点。

：什么叫做“认为是全局最优点”？它不是真正的全局最优点吗？

：不能确保。这样找到的，仍然可能是局部最优点。要想找到全局最优点，还是需要别的更复杂算法，或者与其它算法结合进行。

例如，在爬山情况下，改为允许犯错，即使在局部最优点，伸腿尝试时发生下降，也听之任之，说不定就能慢慢走出局部最优点，重新找到通往真正山顶的路径。

：既然都不能确保找到全局最优点，那鸟群算法比瞎子爬山法好在哪里呢？

：很多情况下，鸟群算法可以更快地找到最优点。这一点，数学上可以证明，大量的实验和实际的工程应用，也可以证实。

可能是因为有一群鸟在行事，它们之间互相协作，集团智慧高于个体智慧嘛。

信天翁的搜索策略

：这样比较，好像不太公平哦。我也可以安排很多个瞎子同时爬山的。

：但是瞎子之间没有通信协作吧。如果允许瞎子之间有协作，那就又有点像是鸟群算法了。

：倒也是。不过，你能否找一个单打独斗的情况，一个瞎子，和一个别的什么，看他们做优化时，谁更厉害？

：是有一些依靠一个个体进行搜索的其它优化算法，只是很少看到哪份资料中比较过它们谁更厉害，我自己也没有实验过。

：你说说看吧。我总觉得瞎子爬山法还有点过于机械，希望还有更聪明的做法。

：如果旷野中的食物稀少，随机分布在一块很大的区域里，动物在搜寻它们时，并不一定是完全漫无目的地随机搜索，那样的效率是比较低的。

科学家们发现，海洋中的掠食者，如皱鳃鲨、黄鳍金枪鱼、蓝色马林、旗鱼，还有信天翁，它们的搜索方式，有一些很独特的特征，即：可能沿某个方向走出很远，才改变方向另搜。

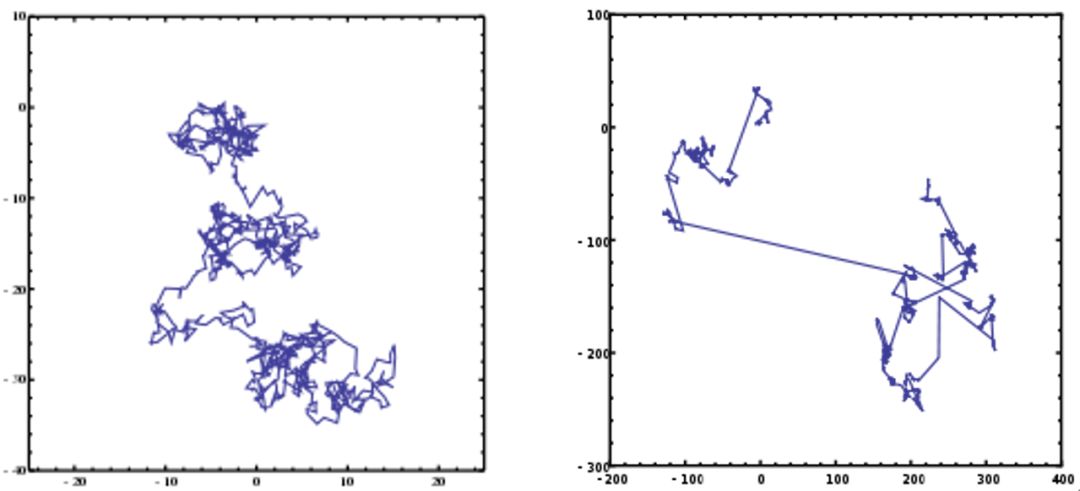
这种搜索方式称为“列维飞行”，是根据法国数学家Lévy的名字命名的。在相同时间内，列维飞行找到的食物数量，很可能高于随机搜索。可能是千百万年的进化，使得他们学会了这种搜索方式。

（左图：随机搜索形成的轨迹   右图：Levy飞行搜索形成的轨迹）

：哦，这倒有点意思。你们可以让计算机也学着这么搜索，快点找到最优解吗？

：已经有人做了。

当算法自己设计算法

：感觉只要是要求“最大”、“最小”、“最优”的问题，就可以用优化算法来做了，对吗？

：基本上可以这么说。其实，优化算法还可以帮我们更多的忙，它不仅授人以鱼，也能授人以渔。

：这是怎么说？

：就好像一个小学生在做数学题，因为掌握的方法不熟练，或者运用的方法不对，做得很慢，旁边坐着的老师，就会指点他改进方法。

：嗯，改进学习方法，这很重要，老师、家长、学生们都在说这个事。

：有一类优化算法，就是可以在一个算法正在工作的时候，随时指点这个工作的算法进行改进的。

：神奇。这回优化的是算法的好坏了。

：此外，我们还面临的一种情况是，已经有很多优化算法，告诉我们如何尽快到达山顶，或者解决别的问题。但优化算法太多了，为什么不用一个优化算法来帮我们选一个呢？

：是啊。我刚才还在琢磨，你说了一大堆优化算法，但是我真正动起手来，也不知道应该用哪一个。

我总不能每一个都去试一下，那样也太耗费时间了。如果有一个算法来帮我选出一种好的，就省事了。

：最后，脑洞不妨再开大一点：如果有一种优化算法，它作为母体，能够自行设计出一个优化算法，使得其在效率上优于所有人工设计出来的优化算法，岂不更妙？

：这……有可能么？

：只要待设计的优化算法本身，能够用数值表示，就好办了。而且已经有一些这方面的研究，也有一些初步成果，似乎还不错。当然，这个过程还有很多困难，理论上也尚待突破。

：那以后都不用借鉴大自然、动物的行为，不需要那么费力地人工地构造那么多的优化算法了，甚至计算机科学家们都可以失业了，是不是？

：还没有那么激进。至少，用于设计优化算法的那些优化算法，我们称之为“元算法”的，还是需要人工设计的。元算法，是关于算法的算法。

：就不能再加多一层，再另外用一个算法来设计元算法，出现一种关于算法的算法的算法，甚至关于算法的算法的算法的算法？

：你还真问倒我了。学术界好像还没有人搞这么多层的，我也不清楚这样做，带来的好处有多大。再看看吧。

：我想起来了，打败世界围棋冠军的AlphaGo，据说是向人类学习，借鉴了几千万局人工对弈的棋谱。

后来的AlphaGo Zero，摆脱对人类的模仿，左右手互搏，自学围棋，最后以100:0的战绩打败它的“前辈”。这个是不是关于算法的算法？

：有一点类似。

：想一想都很恐怖，感觉以后的算法会越来越厉害，它们可以自主设计出算法，比我们人类设计出来的算法更牛，说不定哪天会全面超过人类的智力。

：AI能否超越人类，是一个有争议的话题。今天我们没时间细聊了，留待下次吧。

：好的。

：还是得感谢大自然的馈赠，启发了人类设计出这么多的优化算法，可以用于解决很多的实际问题。就看我们能否很好地利用了。

：就像中医药——人处在大自然的环境中，得了病怎么办，答案还是在大自然中。

*文中图片来源于网络

腾 研 识 者 计 划 招 募

传播常识，寻求共识。

这是腾研识者计划的初心与目标，也是我们对研究这项严肃而重大工作的再定义。

“识者”出自《汉书·师丹传》：“京师识者咸以为宜复丹邑爵，使奉朝请，四方所瞻卬也。” 颜师古注：“识者，谓有识之人也。”，意为有见识的人。

所有人生来都有冲动和好奇，了解我们身处的互联网世界究竟如何运行，以及我们应该如何去理解它，我们同互联网的关系究竟怎样？

我们始终在探索，始终在思考。

我们希望出现有新意的变革者，来重新定义互联网世界的新方法。

正如以赛亚·伯林所说，值得尊敬的知识人是提供理解世界钥匙的人。我们希望腾研识者，就是这样一波肩负重任与理想的人。

回到我们的目标：传播常识，寻求共识。

传播常识，我们不仅需要传统意义上严谨沉稳的钻研者，更需要将高深理论翻译解释得简洁有趣的分享者和连接者。

寻求共识，意味着我们需要打破学科、领域、产业与学术的边界，打破信息茧房、知识结构、数据孤岛等种种壁垒，让更多人参与思想的讨论与砥砺。

我们希望让学术更通俗，让思想更大众。

腾研识者是谁

思考者：深耕学术又渴望打破学术框架的人

分享者：深谙互联网行业又希望把自己的知识传递给聪明的外行的人

变通者：灵活运用书本上知识来处理工作、生活问题的人

跨界者：能够有独立思考能力与跨界思维的人

自荐方式

真诚邀请你加入腾研识者计划，请以“传播常识，寻求共识”为邮件主题，并将此前发表的相关文章和为什么希望成为腾研识者的理由，发送到我们的邮箱

tencentresearch@tencent.com

本期识者

岳亚丁

腾讯公司专家研究员

深圳市科技专家委员会委员

海南省信息化专家咨询委员会委员

  借用各领域技术改进算法提升业务收益的实用主义探索者。

重点关注领域：机器学习、优化算法、时序模型

✉  adenyue@tencent.com

过往文章↓↓↓↓↓↓