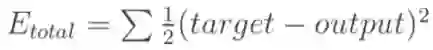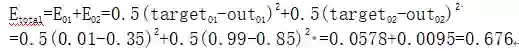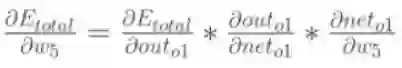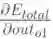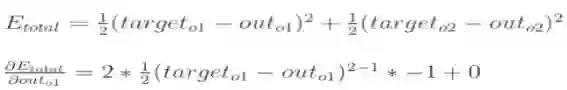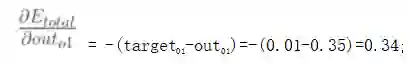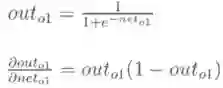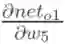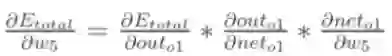ML笔记 |零基础学懂机器学习（三）

机器学习概述

神经网络（有些东西后面会细讲，先在这里说明一下概念和用处）

  a) 生物启发：神经网络是受到大脑对信息的存储和处理方式的启发，大脑的核心组件是神经元，每一个神经元可以通过它的轴突接收来自其他神经元的信息，然后再由该神经元的树突将信息发送给其它神经元，各个神经元之间可是通过突触连接的。

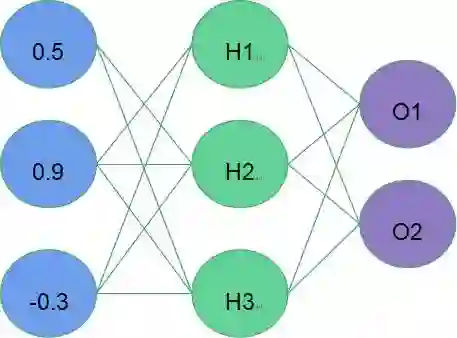
  b) 神经网络架构（如图4）：包含输入层（蓝色）、隐藏层（绿色）和输出层（紫色）。每一层中的神经元接收来自上一层中的神经元的信息，每一个神经元都使用一个函数来处理它的输入并得到一个输出，然后将该输出发送给下一层的神经元。

  c) 激活函数：激活函数被用于每个神经元，激活函数处理神经元的输入并得到输出。最常见的激活函数有sigmoid和Relu，激活函数一般是非线性的。

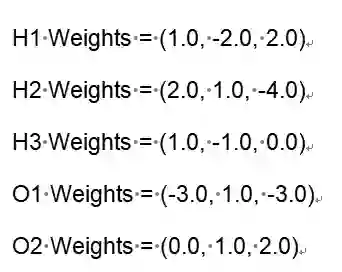
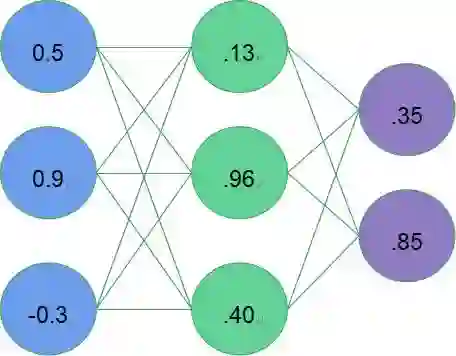
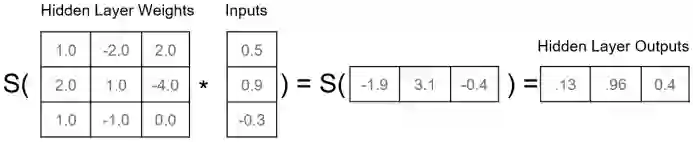
  d) 推理过程：当模型学习好之后，我们如何使用模型对新数据进行推理，以图4为例，蓝色表示输入数据（输入层），绿色是隐藏层，紫色是输出层，输入层与隐藏层的权重用Hi weight表示（i代表神经元），同理，隐藏层与输出层间的权重用Oi weight表示。那么我们可以通过图6中的式子分别得到隐藏层和输出层的值（其中S表示应用于神经元上的激活函数，此处是sigmoid函数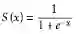：），最终结果如图7示。可见最终得到了.35和.85，如果这是一个分类神经网络，那么我们最终可能会选择输出层的第二个神经元上的标签来对该输入值进行分类。

图4：神经网络架构

图5：层间权重值

图6：隐藏层的计算过程

图7：神经网络推理过程

  e) 矩阵公式：上面输入层到隐藏层的三个计算公式都可以被表示为图8中的矩阵计算。矩阵计算相比上面的计算方式更适合计算机操作，可以极大增强计算并行性。同时GPU因为极好的矩阵计算能力，而被用来为神经网络训练和推理过程加速。

图8：输入层到隐藏层的计算

  f) 训练神经网络步骤：

• 在训练数据集上执行推理过程；

• 计算预测值和训练集真实标签间的误差；

• 确定每个神经元上的误差（利用ii中的误差进行反向传播（back propagation）来计算得到具体每个神经元上的误差）；

• 修改神经网络权重来减小误差（通过梯度下降法实现误差减小）。

  注：神经网络的初始权重是通过随机分配得到的。

  g) 反向传播：求误差与要更新的权重的偏导值，该值即为要更新的误差（数学直观来说，偏导即为一个函数在给定变量所在维度，当前点附近的一个变化率。）。

  h) 梯度下降：梯度下降可以用来减小神经网络的错误，梯度下降在预测值错误很小或者迭代次数已达最大值时结束。每次迭代都要在训练数据上通过最终的预测差值来计算每个权重差值，然后修改权重来减小最终误差。

  i) 最大池化层：因为卷积层产生了大量的输出值，所以简化输出值是非常必要的。最大池化层是从一组数据组提取最大值。

基于梯度的有监督的学习算法（神经网络和许多其他模型）的几个重要函数

  a) 判决规则（decision rule）：y = F(W,X)，表示深度学习的预测值推导过程，即向前传播。式中W表示层间连接的权重值矩阵，X则表示该层的输入向量，函数F（）则是激活函数，例如sigmoid函数。神经网络的每一层都经过这样的一个判决过程，最终得到预测值即预计结果。

  b) 损失函数（loss function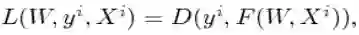）：表示预测值与实际值（标签）之间的距离或者差异，函数D(y,f),表示某种评估实际值y与预测值f间的差异的方式。

  c) 损失梯度（gradient of loss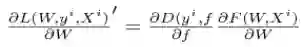）：，该过程是基于损失函数得到的最终误差来计算每个权重值对这个误差的贡献，即通过最终误差来计算每个小误差的过程，也可以叫反向传播（具体看下条）。 

  d) 更新规则（update rule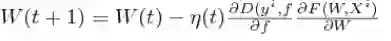）：该过程是将上面计算的每个权重值上的误差用来更新，以得到新的、更为精确的权重值。上式中η(t)是学习率。

  e) 直接解决方案：正规方程（normal equation）：不使用迭代方式，直接计算最优值。

反向传播

  第一条（神经网络-d）中的推理过程即是一个完整的向前传播过程，通过向前传播，我们得到输出值[.35, .85]，与实际值[.01, .99]还相差很远，现在我们对误差进行反向传播，更新权值，重新计算输出。

  a) 计算总误差：（总误差 square error）均差方法计算。 

  因为本例中有两个输出，所以分别计算O1和O2的误差，总误差为两者之和：

  b) 隐藏层到输出层的权重更新。

  为了便于描述，我们将H1、H2、H3与O1间的权重分别称为w4、w5、w6，并查看w5对整体误差产生了多少影响，具体公式如下（链式法则：利用整体误差对w5求偏导）：

其中，out01表示最终结果0.35，net01表示没有进行sigmoid函数之前的结果-0.63，w5是1.0。可以看出我们是按照向前传播的顺序一点一点反向偏导得出具体权重误差，下面我们以w5权重更新为例，具体走一下。

  1.计算

所以

  2.计算

所以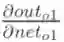= 0.34751053（1-0.34751053）=0.22674696；

  3.计算

  4.三者相乘

= 0.34 *  0.22674696 * 0.96 =0.07401020，

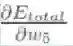
该值即为整体误差对w5的偏导值；

  5.最后我们来更新w5的值：

= 1.0 - 0.5*0.07401020 = 0.96299489 （其中，η是学习率，此处取0.5）

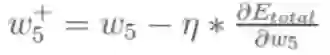
往期笔记：

ML笔记 |零基础学懂机器学习（一）

ML笔记 |零基础学懂机器学习（二）

 【关注本公众号，点击菜单“有奖游戏”，答题抽奖】

---

---

课程咨询｜微信：julyedukefu01

七月热线：010-82712840