简约而又简单的Bloom Filter

上周老王家里有事儿，忙的不行。所以实在没办法缺席了一周，给大家道个歉。也感谢大家的关心，这周重新归队，给大家补上新的内容。（不过接下来一段时间有可能也会请个假，大家理解哈~）

 

言归正传，我们今天要聊的技术呢，其实是一个老掉牙的东东。有多老呢？他是由上个世纪70年代的一个叫布隆的大叔（不对，应该叫大爷了）提出来的，到现在应该快50年了吧。

 

这个技术的名字叫Bloom Filter，中文翻译叫做布隆过滤器。主要用来解决海量数据（注意：这里真真正正是用来解决海量数据）的判重问题。

 

举一个简化的例子（不一定是实际的情况）来说，比如X度的爬虫，去怕了数以亿计的网页，每一个网页都有一个URL。好了，当一个爬虫准备去爬一个网页的时候，要看这个网页是否爬过，最简单的情况就是判断一下这个URL是否在已经爬过的列表里，对吧？那么，这个URL是否存在，怎么判呢？

 

大家可能想到的办法有以下几种：

 

1、每个URL都放入数据库中，判重的时候去查询数据库；

 

2、每个URL都放入类似Memcache或者Redis这样的缓存中，判重的时候去缓存中查询；

 

3、HashTable（HashMap、HashSet）等一类的hash算法；

 

4、And More...

 

以上几种方式，在数据量不是特别大（比如几亿）这些范围内都还是非常work的。如果到百亿或者千亿级别，可能就有点恼火。主要问题是在存储空间 + 算法复杂度（这种数量级，即使是常规索引的O(lnN)算法，也会显得比较的慢）。其实，也不是不可能，比如利用横向+纵向切分，也是可以实现的，只是成本和开发量的问题。

 

当然，为了引出今天的主角，我们得把问题说的难一点（就像写论文，需要指定在非常复杂的条件下，我们的效果最好一样）。这种情况下，Bloom Filter也许就是另外一种解决方案。

 

Bloom Filter的思想也是非常简单。

 

1、建立一个m位的二进制位图。

 

2、选取k中hash算法：h1、h2、h3 ... hk。每个hi的值域在[0, m)之间；

 

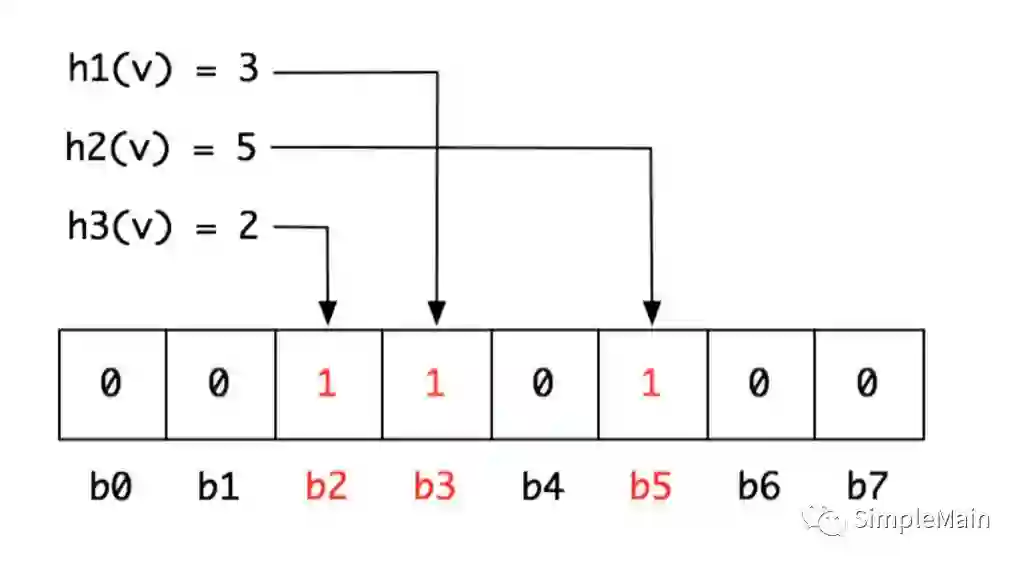
3、当一个值（v）需要放入到存储系统的时候，将这个值进行k次的hash运算，比如：我们将m=8， k=3。就是位图有8个二进制位，然后有3个hash函数。

 

h1(v) = 3

h2(v) = 5

h3(v) = 2

 

这个时候，就将hash值对应的位图的二进制位标记为1。

 

4、判重的时候，来了一个值v'，我们用同样的算法，计算出h1 h2 ... hk，看位图里面是否每一位都被设置成为了1。如果是，则这个v'值很有可能被设置过了。如果不是，则肯定没有被设置过。

 

注意上面飘红的字：如果全为1，则很有可能。为什么？因为Bloom Filter不是一个精确算法，他是一个概率算法。因为hash本身有冲撞，并且位图大小有限，一旦多个值出现冲撞的时候，就肯定会出现误判。但是，如果有一位为0，那么肯定是没有设置过。

 

好了，以上就是Bloom Filter算法的全部。是不是很简单。

 

但是上面留了一个问题：这个很有可能，到底是多有可能？这就涉及到一个不太有趣的概率推算过程（老王一直纠结要不要给讲出来，因为实在是比较枯燥。所以就讲一部分吧。有兴趣的同学可以去网上八一八全部的推导）。

 

====推导开始的分割线 ====

 

1、因为有m个位，所以，某一位设置成1的概率就是 1/m

 

2、那对应的某一位没有设置成1的概率就是 1 - 1/m

 

3、k个哈希函数运算之后都没有设置成1的概率就是 (1 - 1/m)^k

 

4、那如果插入n个值以后，还没有设置成1的概率就是 (1 - 1/m)^kn

 

5、反过来，那插入n个元素以后，这一位设置为1的概率就是 1 - (1 - 1/m)^kn

 

6、如果存在冲撞，那么就需要k个hash值的运算结果都是1，那么这个概率就是[1 - (1 - 1/m)^kn] ^k

 

其实从上面的式子里就能看出，如果m越大，冲撞概率越小。n越大，冲撞概率越大。

 

至于详细的m、k的选择，大家可以根据实际情况到网上选取一个经验值。

 

====推导结束的分割线 ====

 

那拿着这个Bloom Filter我们能做什么呢？

 

其实有比较多的应用场景。比如：我们有n个存储分片，每个存储分片里面存入了大量的信息。当我们要查询某个值的时候，想非常快速判断这个值是否在某个分片里，就可以用Bloom Filter先做一次过滤，这样，绝大多数的值就会很快被检测出来，从而避免去做耗时的查询。

 

还有，比如我们抽取了大量垃圾邮件的特征，当来了一封新的邮件的时候，我们要判断这个新邮件的特征是否有垃圾的可能，就可以用Bloom Filter先存储这些特征。来新邮件以后，就可以最简单的判断一下，这样效率非常的高。避免去做耗时的查询。

 

好了，如果在遇到大数据量，又没有精确要求的场景下，可以用这种方式来做一些初步的过滤。算法本身简单，实现难度也不是很大。但是效果还不错。大家觉得呢？