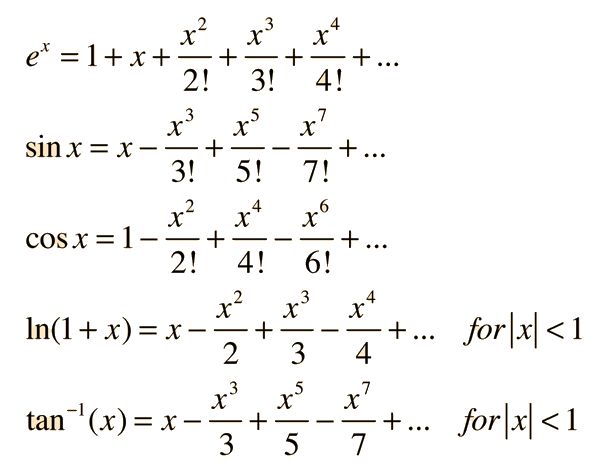基于Numpy实现同态加密神经网络
编者按:在分布式AI环境下,同态加密神经网络有助于保护商业公司知识产权和消费者隐私。让我们和DeepMind数据科学家、Udacity深度学习导师Andrew Trask一起,来看看如何基于Numpy实现同态加密神经网络吧。
TLDR: 在这篇文章中,我们将训练一个在训练阶段完全加密的神经网络(在未加密的数据上训练)。得到的神经网络将具备两个有益的性质。首先,保护神经网络的智能免遭窃取,使有价值的AI可以在不安全的环境中加以训练而不用冒智能遭窃的风险。其次,网络只能进行加密预测(大概对外部世界毫无影响,因为在没有密钥的情况下,外部世界无法理解预测)。这在用户和超智能间构成了一个有价值的权力失衡。如果AI是同态加密的,那么在AI看来,整个外部世界也是同态加密的。一个控制密钥的人类可以选择解锁AI本身(将AI释放到世界中)或仅仅解密AI做出的单个预测(看起来更安全)。
当我写完新文章后,我通常会发推说一下。如果你对我的文章感兴趣,欢迎关注 @iamtrask,也欢迎向我反馈。
如果你对训练加密神经网络感兴趣,可以看看OpenMined的PySyft库。
超智能
很多人都担忧超智能有一天会选择伤害人类。史蒂芬·霍金曾呼吁建立新的世界政府来管理我们赋予人工智能的能力,以防人工智能最终摧毁人类。这些是相当大胆的主张,我认为它们反映了科学界和整个世界对这一问题的普遍担忧。本文将是一篇介绍解决这一问题的潜在技术方案的教程,我将通过一些玩具样例代码来演示这一方法。
目标很简单。我们想要创建未来会变得非常智能的AI技术(智能到可以解决治愈癌症、终结世界上的饥饿等问题),但是这样的智能受人类的控制(基于密钥),因而其智能的应用是受限的。不受限的学习是很棒的,但知识的不受限的应用可能具有潜在危险性。
为了介绍这一想法,让我先简要介绍两个非常激动人心的研究领域:深度学习和同态加密。
一、什么是深度学习?
深度学习是用于自动化智能的工具套件,主要基于神经网络。这一计算机科学的领域,是最近AI技术爆发的主要动力,因为深度学习在许多智能任务上超越了先前的表现记录。例如,他是DeepMind的AlphaGo系统的主要组成部分。
神经网络基于输入做出预测。它通过试错法学习做出有效的预测。刚开始,它做出一个预测(起初基本上是随机预测),接着接收一个“错误信号”,该信号表明它的预测过高或过低(通常是概率)。在这一周期重复数百万次后,网络开始搞明白情况。想要了解更多神经网络如何工作的细节,请参考基于Numpy实现神经网络:反向传播一文。
这里最神奇的是错误信号。如果不告知预测的表现有多好,神经网络无法学习。牢记这一点。
二、什么是同态加密?
顾名思义,同态加密是一种加密的形式。在不对称情形下,它可以接受完全可读的文本,然后基于“公钥”将其转变为乱码。更重要的是,它可以基于“私钥”将乱码转回同样的文本。然而,除非你有“私钥”,(理论上)你无法解码加密后的乱码。
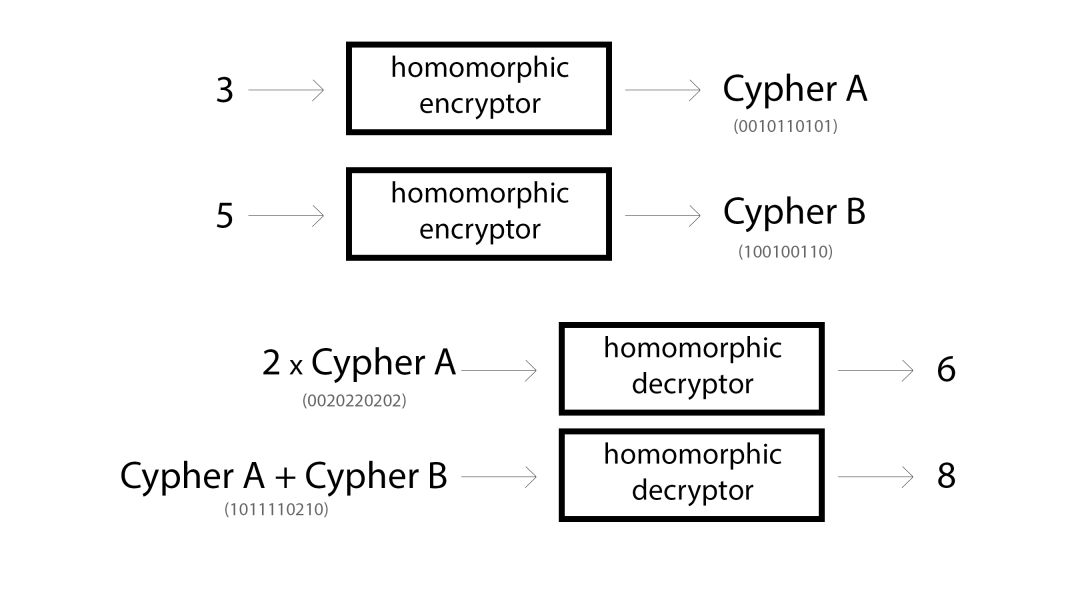
同态加密是一种特殊形式的加密。它允许某人在无法阅读信息的前提下以特定的方式修改加密信息。例如,同态加密可以应用于数字上,让加密过的数字可以进行乘法和加法运算而无需解密数字。下面是一些玩具样例。
现在出现了越来越多的同态加密方案,各有不同的性质。这是一个相对年轻的领域,仍有一些明显的问题有待解决,不过我们将这些内容留待以后讨论。
就目前而言,让我们从整数公钥加密方案开始。整数公钥加密方案是一种乘法和加法上的同态加密,允许进行上图的操作。不仅如此,由于公钥允许“单向”加密,你甚至可以进行未加密数字和加密数字间的运算(通过单向加密),上图的2 * Cypher A就是一个例子。(某些加密方案甚至不要求这一点……不过同样……我们以后讨论这个。)
三、我们可以结合这两者吗?
也许深度学习和同态加密之间最频繁的互动体现在数据隐私上。当你同态加密数据时,你无法读取数据但仍然可以保持大多数有趣的统计学结构。这让人们得以在加密数据上训练模型(CryptoNets)。甚至有一家名为Numer.ai的初创对冲基金加密昂贵的专有数据,允许任何人尝试训练机器学习模型预测股票市场。通常这不可能办到,因为会导致放弃极为昂贵的信息(不可能基于通常的加密数据训练模型)。
然而,本文将反其道而行,加密神经网络,然后在解密信息上加以训练。
复杂度惊人的神经网络,事实上可以划分成很少(少得惊人)几种组件,这些组件不断重复以构成神经网络。其实,仅仅基于如下操作,就可以创建很多最先进的神经网络:
加法
乘法
除法
减法
Sigmoid
Tanh
指数函数
那么,让我们提出这一明显的技术问题,我们能否同态加密神经网络本身?我们会想这么做吗?结果发现,基于一些保守的逼近,这是可以办到的。
加法 —— 开箱即用
乘法 —— 开箱即用
除法 —— 开箱即用?只是乘法的倒数
加法 —— 开箱即用?只是加上负数
Sigmoid —— 嗯……也许有点难度
Tanh —— 嗯……也许有点难度
指数函数 —— 嗯……也许有点难度
看起来实现除法和减法会是相当微不足道的事情,但那些更复杂的函数就……好吧……比简单的加法和乘法更复杂。为了尝试同态加密一个深度神经网络,我们还需要一个秘密原料。
四、泰勒级数展开
也许你在小学学过,泰勒级数允许我们使用无限项加法、减法、乘法、除法来计算一个复杂(非线性)函数。这很完美!(除了无限部分)。幸运的是,如果你早早地停止了计算精确的泰勒级数展开,你仍然能得到手头的函数的一个逼近值。下面是通过泰勒级数逼近一些流行函数的例子(来源)。
等下!这里有指数!别担心。指数不过是反复相乘。下面是使用泰勒级数逼近sigmoid函数的python实现(相关公式见Wolfram Alpha)。我们将选取级数的开始几项,看看能逼近到什么程度。
import numpy as np
def sigmoid_exact(x):
return 1 / (1 + np.exp(-x))
# 使用泰勒级数
def sigmoid_approximation(x):
return (1 / 2) + (x / 4) - (x**3 / 48) + (x**5 / 480)
for lil_number in [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]:
print("\n输入:" + str(lil_number))
print("精确的Sigmoid值:" + str(sigmoid_exact(lil_number)))
print("逼近Sigmoid:" + str(sigmoid_approximation(lil_number)))
结果:
输入:0.1
精确的Sigmoid值:0.52497918747894
逼近Sigmoid:0.5249791874999999
输入:0.2
精确的Sigmoid值:0.549833997312478
逼近Sigmoid:0.549834
输入:0.3
精确的Sigmoid值:0.574442516811659
逼近Sigmoid:0.5744425624999999
输入:0.4
精确的Sigmoid值:0.598687660112452
逼近Sigmoid:0.598688
输入:0.5
精确的Sigmoid值:0.6224593312018546
逼近Sigmoid:0.6224609375000001
输入:0.6
精确的Sigmoid值:0.6456563062257954
逼近Sigmoid:0.6456620000000001
输入:0.7
精确的Sigmoid值:0.6681877721681662
逼近Sigmoid:0.6682043125000001
输入:0.8
精确的Sigmoid值:0.6899744811276125
逼近Sigmoid:0.690016
输入:0.9
精确的Sigmoid值:0.7109495026250039
逼近Sigmoid:0.7110426875
输入:1.0
精确的Sigmoid值:0.7310585786300049
逼近Sigmoid:0.73125
仅仅使用了泰勒级数的前4项,我们已经相当逼近sigmoid函数了。既然我们已经具备了通用的策略,是时候选择一个同态加密算法了。
五、选择加密算法
同态加密是一个相对较新的领域,其中的主要里程碑是Craig Gentry在2009年发现的第一个全同态加密算法。这一里程碑为许多后来者建立了据点。大部分关于同态加密的激动人心的研究围绕开发图灵完备的同态加密计算机展开。因此,对全同态加密方案的需求让人们试图找到一个算法,使得进行任意计算所需的多种逻辑门都可以通这一算法高效而安全地计算。大体的希望是人们能够安全地将工作放到云端,而不必冒发送到云端的数据被发送者以外的人读取的风险。这是一个非常酷的想法,也取得了很多进展。
然而,这一角度存在一些缺陷。一般而言,相比普通电脑,大多数全同态加密方案慢得让人怀疑人生(目前还不实用)。这鼓舞了一系列有趣的研究,将操作种类限制为某种程度上同态,这样至少可以进行某些操作。不那么灵活,但是更快,这是常见的计算上的折衷。
这是我们想要开始查看的地方。理论上,我们想要一个操作浮点数的同态加密方案(不过很快我们将看到,最终我们选择了操作整数的方案),而不是操作二进制值的方案。二进制可以工作,但它不仅要求全同态加密的灵活性(以性能为代价),还要求我们管理二进制表示和我们想要计算的数学运算之间的逻辑。一个不那么强大,为浮点运算定制的HE(HE为同态加密Homomorphic Encryption的缩写)算法会更合适。
尽管加上了这一限制,仍有非常多的选择。下面是一些具备我们需要的特性的流行算法:
Efficient Homomorphic Encryption on Integer Vectors and Its Applications(基于整数向量的高效同态加密及其应用)
Yet Another Somewhat Homomorphic Encryption (YASHE)(又一个某种程度上的同态加密)
Somewhat Practical Fully Homomorphic Encryption (FV)(某种程度上实用的全同态加密)
Fully Homomorphic Encryption without Bootstrapping(非自举的全同态加密)
最佳的选择可能是YASHE或FV。YASHE是流行的CryptoNet使用的算法,对浮点运算的支持很棒。然而,它相当复杂。为了让这篇文章容易阅读、便于尝试,我们将选择稍微不那么高级(可能也不那么安全)的Efficient Integer Vector Homomorphic Encryption(高效整数向量同态加密)。然而,我认为非常值得指出的是,在你阅读本文的时候,更多新的HE算法正在开发之中,同时本文展示的想法通用于任何在整数或浮点数的加法和乘法上同态加密的方案。甚至说,我的愿望是引起对HE的这一应用的关注,以便更多的为深度学习优化的HE算法能被开发出来。
Yu、Lai、Paylor的论文Efficient Integer Vector Homomorphic Encryption详细描述了这一算法,相应的实现可以在GitHub上获取(jamespayor/vector-homomorphic-encryption)。主要部分在C++文件vhe.cpp中。下面我们引导读者阅读代码的一个python移植,说明代码是干什么的。如果你选择实现一个更高级的方案,这也会很有帮助,因为有一些主题相对而言是通用的(一般函数名,变量名,等等)。
六、Python中的同态加密
首先是一些同态加密术语:
明文(plaintext) 未加密数据。也叫“消息”。在我们的例子中,这将是一些表示神经网络的数字。
密文(cyphertext) 加密数据。我们将在密文之上进行数学运算,这些运算会改变底层的明文。
公钥(public key) 伪随机数字序列,让任何人得以加密数据。可以和别人分享,因为(理论上)公钥只能用于加密。
私钥/密钥(private/secret key) 伪随机数字序列,让你解密被公钥加密的数据。你不想和别人分享私钥。否则,别人可以解密你的消息。
对应的变量名(不同的同态加密技术都倾向于使用这些标准变量名):
S 表示密钥/私钥的矩阵。用于解密。
M 公钥。用于加密和进行数学运算。在有些算法中,不是所有数学运算都需要公钥。但这一算法非常广泛地使用公钥。
c 加密数据向量,密文。
x 消息,即明文。有些论文使用
m作明文的变量名。w 单个“加权(weighting)”标量变量,用于重加权输入消息x(让它一致地更长或更短)。这一变量用于调节信噪比。加强信号后,对于给定的操作而言,消息较不容易受噪声影响。然而,过于加强信号,会增加完全毁坏数据的概率。这是一个平衡。
E或e 一般指随机噪声。在某些情形下,指用公钥加密数据前添加的噪声。一般而言,噪声使解密更困难。噪声使同一消息的两次加密可以不一样,在让消息难以破解方面,这很重要。注意,取决于算法和实现,这可能是一个向量,也可能是一个矩阵。在其他情形下,指随操作积累的噪声,详见后文。
和许多数学论文的惯用法一样,大写字母对应矩阵,小写字母对应向量,斜体小写对应标量。我们关注同态加密的四种操作:公私钥对生成,单向加密,解密,数学运算。让我们从解密开始。
左边的公式描述了密钥S和消息x的一般关系。右边的公式显示了如何使用密钥解密消息。不知道你注意到没有,右边的公式并不包含e。基本上,同态加密技术一般引入足够多的噪声使没有密钥的情况下难以破解出原始消息,但是引入的噪声的量又足够少,当你确实具有密钥时噪声可以通过取整忽略。右边的公式中的框表示“取整到最接近的整数”。其他同态加密算法使用不同的取整。模数运算几乎普遍存在。而加密则生成使上述关系为真的c. 如果S是一个随机矩阵,那么c很难解密。一个简单的、非对称的生成加密钥的方式是找到密钥的逆矩阵。让我们看下相应的Python代码。
import numpy as np
def generate_key(w,m,n):
S = (np.random.rand(m,n) * w / (2 ** 16)) # 可证明 max(S) < w
return S
def encrypt(x,S,m,n,w):
assert len(x) == len(S)
e = (np.random.rand(m)) # 可证明 max(e) < w / 2
c = np.linalg.inv(S).dot((w * x) + e)
return c
def decrypt(c,S,w):
return (S.dot(c) / w).astype('int')
x = np.array([0,1,2,5])
m = len(x)
n = m
w = 16
S = generate_key(w,m,n)
你可以在Jupyter Notebook中试着运行上面的代码,进行一些操作:
注意,我们可以对密文进行一些基本的运算,这些运算改动了相应的明文。很优雅,不是吗?
七、优化加密
重要一课: 回顾一下之前的公式。如果密钥S是一个单位矩阵,那么c不过是输入x的一个重加权的、略带噪声的版本。如果你不明白上面的话,请Google“单位矩阵教程”。限于篇幅,这里就不详细介绍单位矩阵了。
这引导我们思考加密是如何进行的。论文作者没有显式地分配一对独立的“公钥”和“私钥”,相反,提出了一种“钥交换”技术,将私钥S替换为S'。更具体地,这一私钥交换技术涉及生成一个可以进行该变换的矩阵M。由于M具备将消息从未加密状态(单位矩阵密钥)转换为加密状态(随机而难以猜测的密钥),这个M矩阵正好可以用作我们的公钥!
上面一段话包含许多信息,我们也许讲得太快了。让我们重新概括一下。
发生了什么……
基于上面两个公式,如果密钥是一个单位矩阵,那么消息是未加密的。
基于上面两个公式,如果密钥是一个随机矩阵,那么消息是加密的。
我们构造一个矩阵M将一个密钥转换为另一个私钥。
当矩阵M将单位矩阵转换为一个随机密钥时,根据定义,它使用单向加密方式加密了消息。
由于M充当了“单向加密”的角色,我们称它为“公钥”,并且可以像公钥一样分发它,因为它无法用于解密。
好了,不多拖延了,让我们看下这一切是如何通过Python实现的。
import numpy as np
def generate_key(w,m,n):
S = (np.random.rand(m,n) * w / (2 ** 16)) # 可证明 max(S) < w
return S
def encrypt(x,S,m,n,w):
assert len(x) == len(S)
e = (np.random.rand(m)) # 可证明 max(e) < w / 2
c = np.linalg.inv(S).dot((w * x) + e)
return c
def decrypt(c,S,w):
return (S.dot(c) / w).astype('int')
def get_c_star(c,m,l):
c_star = np.zeros(l * m,dtype='int')
for i in range(m):
b = np.array(list(np.binary_repr(np.abs(c[i]))),dtype='int')
if(c[i] < 0):
b *= -1
c_star[(i * l) + (l-len(b)): (i+1) * l] += b
return c_star
def switch_key(c,S,m,n,T):
l = int(np.ceil(np.log2(np.max(np.abs(c)))))
c_star = get_c_star(c,m,l)
S_star = get_S_star(S,m,n,l)
n_prime = n + 1
S_prime = np.concatenate((np.eye(m),T.T),0).T
A = (np.random.rand(n_prime - m, n*l) * 10).astype('int')
E = (1 * np.random.rand(S_star.shape[0],S_star.shape[1])).astype('int')
M = np.concatenate(((S_star - T.dot(A) + E),A),0)
c_prime = M.dot(c_star)
return c_prime,S_prime
def get_S_star(S,m,n,l):
S_star = list()
for i in range(l):
S_star.append(S*2**(l-i-1))
S_star = np.array(S_star).transpose(1,2,0).reshape(m,n*l)
return S_star
def get_T(n):
n_prime = n + 1
T = (10 * np.random.rand(n,n_prime - n)).astype('int')
return T
def encrypt_via_switch(x,w,m,n,T):
c,S = switch_key(x*w,np.eye(m),m,n,T)
return c,S
x = np.array([0,1,2,5])
m = len(x)
n = m
w = 16
S = generate_key(w,m,n)
上面的代码的基本思路是让S大体上是单位矩阵,然后在其之上连接一个随机向量T。因此T具备所有密钥所需的信息,不过我们仍然需要构建一个尺寸为S的矩阵使得一切可以工作。
八、创建一个XOR神经网络
既然我们已经知道如何加密和解密消息(以及进行基本的加法和乘法计算),是时候尝试扩展剩余的运算,以便构建一个简单的XOR神经网络。尽管从技术上说,神经网络不过是一系列非常简单的操作,我们还是需要一些操作的组合以实现便利的功能。下面我将描述我们需要的每项操作,以及在一个较高的抽象层次上,我们是如何实现这些操作的(基本上是我们将使用的加法和乘法的序列)。接着我会向你展示代码。关于一些细节,请参考前面提到的论文。
浮点数 我们将简单地scale浮点数到整数。我们将在整数上训练我们的网络(把整数当成浮点数)。比如,假设
scale=1000,0.2 * 0.5 = 0.1就是200 * 500 = 100000。还原时,100000 / (1000 * 1000) = 0.1(因为我们使用了乘法,所以需要除以1000的平方)。初看起来这很有技巧性,但你会适应的。由于我们使用的HE方案取整到最接近的整数,这也让我们得以控制神经网络的精度。向量矩阵乘法 这是我们的黄油面包(最基本的操作)。事实上,转换密钥的矩阵M是一种线性变换的方式。
内积 在合适的背景下,上述线性变换可能是内积。
sigmoid 由于我们可以进行向量矩阵乘法运算,基于足够的乘法,我们可以演算任意多项式的值。因为我们已经知道了对应sigmoid的泰勒级数多项式,我们可以演算sigmoid的逼近值!
逐元素矩阵乘法 这一操作惊人地低效。我们需要进行向量矩阵乘法或一系列内积运算。
外积 我们可以通过掩码和内积完成这一运算。
声明一下,可能存在完成这些运算的更高效的方法,但我不想冒打破同态加密方案完整性的风险。所以某种程度上我是通过论文中提供的函数来反推如何完成上述运算的(除了算法容许的sigmoid扩展)。现在,让我们看看完成这些的Python代码:
def sigmoid(layer_2_c):
out_rows = list()
for position in range(len(layer_2_c)-1):
M_position = M_onehot[len(layer_2_c)-2][0]
layer_2_index_c = innerProd(layer_2_c,v_onehot[len(layer_2_c)-2][position],M_position,l) / scaling_factor
x = layer_2_index_c
x2 = innerProd(x,x,M_position,l) / scaling_factor
x3 = innerProd(x,x2,M_position,l) / scaling_factor
x5 = innerProd(x3,x2,M_position,l) / scaling_factor
x7 = innerProd(x5,x2,M_position,l) / scaling_factor
xs = copy.deepcopy(v_onehot[5][0])
xs[1] = x[0]
xs[2] = x2[0]
xs[3] = x3[0]
xs[4] = x5[0]
xs[5] = x7[0]
out = mat_mul_forward(xs,H_sigmoid[0:1],scaling_factor)
out_rows.append(out)
return transpose(out_rows)[0]
def load_linear_transformation(syn0_text,scaling_factor = 1000):
syn0_text *= scaling_factor
return linearTransformClient(syn0_text.T,getSecretKey(T_keys[len(syn0_text)-1]),T_keys[len(syn0_text)-1],l)
def outer_product(x,y):
flip = False
if(len(x) < len(y)):
flip = True
tmp = x
x = y
y = tmp
y_matrix = list()
for i in range(len(x)-1):
y_matrix.append(y)
y_matrix_transpose = transpose(y_matrix)
outer_result = list()
for i in range(len(x)-1):
outer_result.append(mat_mul_forward(x * onehot[len(x)-1][i],y_matrix_transpose,scaling_factor))
if(flip):
return transpose(outer_result)
return outer_result
def mat_mul_forward(layer_1,syn1,scaling_factor):
input_dim = len(layer_1)
output_dim = len(syn1)
buff = np.zeros(max(output_dim+1,input_dim+1))
buff[0:len(layer_1)] = layer_1
layer_1_c = buff
syn1_c = list()
for i in range(len(syn1)):
buff = np.zeros(max(output_dim+1,input_dim+1))
buff[0:len(syn1[i])] = syn1[i]
syn1_c.append(buff)
layer_2 = innerProd(syn1_c[0],layer_1_c,M_onehot[len(layer_1_c) - 2][0],l) / float(scaling_factor)
for i in range(len(syn1)-1):
layer_2 += innerProd(syn1_c[i+1],layer_1_c,M_onehot[len(layer_1_c) - 2][i+1],l) / float(scaling_factor)
return layer_2[0:output_dim+1]
def elementwise_vector_mult(x,y,scaling_factor):
y =[y]
one_minus_layer_1 = transpose(y)
outer_result = list()
for i in range(len(x)-1):
outer_result.append(mat_mul_forward(x * onehot[len(x)-1][i],y,scaling_factor))
return transpose(outer_result)[0]
有一点我之前没有告诉你。为了节省时间,我预计算了一些钥、向量、矩阵,并对它们作了排序。这包括完全由1组成的向量,不同长度的one-hot编码向量。这有助于上面的掩码操作,以及其他我们希望可以做到的简单操作。例如,sigmoid的导数是sigmoid(x) * (1 - sigmoid(x))。因此,预计算这些变量会很方便。下面是预计算步骤。
# 在安全的服务端进行
l = 100
w = 2 ** 25
aBound = 10
tBound = 10
eBound = 10
max_dim = 10
scaling_factor = 1000
# 钥
T_keys = list()
for i in range(max_dim):
T_keys.append(np.random.rand(i+1,1))
# 单向加密变换
M_keys = list()
for i in range(max_dim):
M_keys.append(innerProdClient(T_keys[i],l))
M_onehot = list()
for h in range(max_dim):
i = h+1
buffered_eyes = list()
for row in np.eye(i+1):
buffer = np.ones(i+1)
buffer[0:i+1] = row
buffered_eyes.append((M_keys[i-1].T * buffer).T)
M_onehot.append(buffered_eyes)
c_ones = list()
for i in range(max_dim):
c_ones.append(encrypt(T_keys[i],np.ones(i+1), w, l).astype('int'))
v_onehot = list()
onehot = list()
for i in range(max_dim):
eyes = list()
eyes_txt = list()
for eye in np.eye(i+1):
eyes_txt.append(eye)
eyes.append(one_way_encrypt_vector(eye,scaling_factor))
v_onehot.append(eyes)
onehot.append(eyes_txt)
H_sigmoid_txt = np.zeros((5,5))
H_sigmoid_txt[0][0] = 0.5
H_sigmoid_txt[0][1] = 0.25
H_sigmoid_txt[0][2] = -1/48.0
H_sigmoid_txt[0][3] = 1/480.0
H_sigmoid_txt[0][4] = -17/80640.0
H_sigmoid = list()
for row in H_sigmoid_txt:
H_sigmoid.append(one_way_encrypt_vector(row))
如果你仔细查看了上面的代码,你会注意到H_sigmoid矩阵是我们需要的用于演算sigmoid多项式的矩阵。最后,我们使用如下代码训练我们的神经网络。如果不明白神经网络的部分,你可以温习下基于Numpy实现神经网络:反向传播一文。我基本上使用了文中的XOR网络,使用适当的工具函数替换了其中一些操作,以加密权重。
np.random.seed(1234)
input_dataset = [[],[0],[1],[0,1]]
output_dataset = [[0],[1],[1],[0]]
input_dim = 3
hidden_dim = 4
output_dim = 1
alpha = 0.015
# 使用公钥单向加密训练数据(可就地进行)
y = list()
for i in range(4):
y.append(one_way_encrypt_vector(output_dataset[i],scaling_factor))
# 生成权重
syn0_t = (np.random.randn(input_dim,hidden_dim) * 0.2) - 0.1
syn1_t = (np.random.randn(output_dim,hidden_dim) * 0.2) - 0.1
# 单向加密权重
syn1 = list()
for row in syn1_t:
syn1.append(one_way_encrypt_vector(row,scaling_factor).astype('int64'))
syn0 = list()
for row in syn0_t:
syn0.append(one_way_encrypt_vector(row,scaling_factor).astype('int64'))
# 开始训练
for iter in range(1000):
decrypted_error = 0
encrypted_error = 0
for row_i in range(4):
if(row_i == 0):
layer_1 = sigmoid(syn0[0])
elif(row_i == 1):
layer_1 = sigmoid((syn0[0] + syn0[1])/2.0)
elif(row_i == 2):
layer_1 = sigmoid((syn0[0] + syn0[2])/2.0)
else:
layer_1 = sigmoid((syn0[0] + syn0[1] + syn0[2])/3.0)
layer_2 = (innerProd(syn1[0],layer_1,M_onehot[len(layer_1) - 2][0],l) / float(scaling_factor))[0:2]
layer_2_delta = add_vectors(layer_2,-y[row_i])
syn1_trans = transpose(syn1)
one_minus_layer_1 = [(scaling_factor * c_ones[len(layer_1) - 2]) - layer_1]
sigmoid_delta = elementwise_vector_mult(layer_1,one_minus_layer_1[0],scaling_factor)
layer_1_delta_nosig = mat_mul_forward(layer_2_delta,syn1_trans,1).astype('int64')
layer_1_delta = elementwise_vector_mult(layer_1_delta_nosig,sigmoid_delta,scaling_factor) * alpha
syn1_delta = np.array(outer_product(layer_2_delta,layer_1)).astype('int64')
syn1[0] -= np.array(syn1_delta[0]* alpha).astype('int64')
syn0[0] -= (layer_1_delta).astype('int64')
if(row_i == 1):
syn0[1] -= (layer_1_delta).astype('int64')
elif(row_i == 2):
syn0[2] -= (layer_1_delta).astype('int64')
elif(row_i == 3):
syn0[1] -= (layer_1_delta).astype('int64')
syn0[2] -= (layer_1_delta).astype('int64')
# 如果有安全性要求,可以将加密的损失发送到别处解密。
encrypted_error += int(np.sum(np.abs(layer_2_delta)) / scaling_factor)
decrypted_error += np.sum(np.abs(s_decrypt(layer_2_delta).astype('float')/scaling_factor))
sys.stdout.write("\r 迭代" + str(iter) + " 加密损失:" + str(encrypted_error) + " 解密损失:" + str(decrypted_error) + " Alpha:" + str(alpha))
# 让日志好看一点
if(iter % 10 == 0):
print()
# 加密误差达到一定水平后停止训练
if(encrypted_error < 25000000):
break
print("\n最终预测:")
for row_i in range(4):
if(row_i == 0):
layer_1 = sigmoid(syn0[0])
elif(row_i == 1):
layer_1 = sigmoid((syn0[0] + syn0[1])/2.0)
elif(row_i == 2):
layer_1 = sigmoid((syn0[0] + syn0[2])/2.0)
else:
layer_1 = sigmoid((syn0[0] + syn0[1] + syn0[2])/3.0)
layer_2 = (innerProd(syn1[0],layer_1,M_onehot[len(layer_1) - 2][0],l) / float(scaling_factor))[0:2]
print("真预测:" + str(output_dataset[row_i]) + " 加密预测:" + str(layer_2) + " 解密预测:" + str(s_decrypt(layer_2) / scaling_factor))
迭代0 加密损失:84890656 解密损失:2.529 Alpha:0.015
迭代10 加密损失:69494197 解密损失:2.071 Alpha:0.015
迭代20 加密损失:64017850 解密损失:1.907 Alpha:0.015
迭代30 加密损失:62367015 解密损失:1.858 Alpha:0.015
迭代40 加密损失:61874493 解密损失:1.843 Alpha:0.015
迭代50 加密损失:61399244 解密损失:1.829 Alpha:0.015
迭代60 加密损失:60788581 解密损失:1.811 Alpha:0.015
迭代70 加密损失:60327357 解密损失:1.797 Alpha:0.015
迭代80 加密损失:59939426 解密损失:1.786 Alpha:0.015
迭代90 加密损失:59628769 解密损失:1.778 Alpha:0.015
迭代100 加密损失:59373621 解密损失:1.769 Alpha:0.015
迭代110 加密损失:59148014 解密损失:1.763 Alpha:0.015
迭代120 加密损失:58934571 解密损失:1.757 Alpha:0.015
迭代130 加密损失:58724873 解密损失:1.75 Alpha:0.0155
迭代140 加密损失:58516008 解密损失:1.744 Alpha:0.015
迭代150 加密损失:58307663 解密损失:1.739 Alpha:0.015
迭代160 加密损失:58102049 解密损失:1.732 Alpha:0.015
迭代170 加密损失:57863091 解密损失:1.725 Alpha:0.015
迭代180 加密损失:55470158 解密损失:1.653 Alpha:0.015
迭代190 加密损失:54650383 解密损失:1.629 Alpha:0.015
迭代200 加密损失:53838756 解密损失:1.605 Alpha:0.015
迭代210 加密损失:51684722 解密损失:1.541 Alpha:0.015
迭代220 加密损失:54408709 解密损失:1.621 Alpha:0.015
迭代230 加密损失:54946198 解密损失:1.638 Alpha:0.015
迭代240 加密损失:54668472 解密损失:1.63 Alpha:0.0155
迭代250 加密损失:55444008 解密损失:1.653 Alpha:0.015
迭代260 加密损失:54094286 解密损失:1.612 Alpha:0.015
迭代270 加密损失:51251831 解密损失:1.528 Alpha:0.015
迭代276 加密损失:24543890 解密损失:0.732 Alpha:0.015
最终预测:
真实预测:[0] 加密预测:[-3761423723.0718255 0.0] 解密预测:[-0.112]
真实预测:[1] 加密预测:[24204806753.166267 0.0] 解密预测:[ 0.721]
真实预测:[1] 加密预测:[23090462896.17028 0.0] 解密预测:[ 0.688]
真实预测:[0] 加密预测:[1748380342.4553354 0.0] 解密预测:[ 0.052]
以上是我训练神经网络时看到的输出。加密噪声的某种组合和低精度导致某种程度上笨重的学习,因此调优具有一定的技巧性。训练也相当慢。这些很大程度上是因为转置运算非常昂贵。我比较确定本可以通过更简单的操作完成转置运算,但是,如前所述,像这样证明概念可行的代码,我更偏向安全性。
小小的总结
网络的权重都是加密的。
数据解密为1和0.
经过训练后,可以解密网络,以提高性能或进行进一步的训练(或者转用不同的加密钥)。
训练损失和输出预测同样是加密过的值。我们需要解码之后才能解读网络表现。
九、情感分类
下面是一个真实一些的例子,我们在IMDB评论情感数据上训练同态加密的网络,网络基于Udacity的深度学习课程。完整代码发布在GitHub上。
import time
import sys
import numpy as np
# 调整之前的网络以建模这些现象
class SentimentNetwork:
def __init__(self, reviews,labels,min_count = 10,polarity_cutoff = 0.1,hidden_nodes = 8, learning_rate = 0.1):
np.random.seed(1234)
self.pre_process_data(reviews, polarity_cutoff, min_count)
self.init_network(len(self.review_vocab),hidden_nodes, 1, learning_rate)
def pre_process_data(self,reviews, polarity_cutoff,min_count):
print("Pre-processing data...")
positive_counts = Counter()
negative_counts = Counter()
total_counts = Counter()
for i in range(len(reviews)):
if(labels[i] == 'POSITIVE'):
for word in reviews[i].split(" "):
positive_counts[word] += 1
total_counts[word] += 1
else:
for word in reviews[i].split(" "):
negative_counts[word] += 1
total_counts[word] += 1
pos_neg_ratios = Counter()
for term,cnt in list(total_counts.most_common()):
if(cnt >= 50):
pos_neg_ratio = positive_counts[term] / float(negative_counts[term]+1)
pos_neg_ratios[term] = pos_neg_ratio
for word,ratio in pos_neg_ratios.most_common():
if(ratio > 1):
pos_neg_ratios[word] = np.log(ratio)
else:
pos_neg_ratios[word] = -np.log((1 / (ratio + 0.01)))
review_vocab = set()
for review in reviews:
for word in review.split(" "):
if(total_counts[word] > min_count):
if(word in pos_neg_ratios.keys()):
if((pos_neg_ratios[word] >= polarity_cutoff) or (pos_neg_ratios[word] <= -polarity_cutoff)):
review_vocab.add(word)
else:
review_vocab.add(word)
self.review_vocab = list(review_vocab)
label_vocab = set()
for label in labels:
label_vocab.add(label)
self.label_vocab = list(label_vocab)
self.review_vocab_size = len(self.review_vocab)
self.label_vocab_size = len(self.label_vocab)
self.word2index = {}
for i, word in enumerate(self.review_vocab):
self.word2index[word] = i
self.label2index = {}
for i, label in enumerate(self.label_vocab):
self.label2index[label] = i
def init_network(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
# 设置输入层、隐藏层、输出层节点数
self.input_nodes = input_nodes
self.hidden_nodes = hidden_nodes
self.output_nodes = output_nodes
print("Initializing Weights...")
self.weights_0_1_t = np.zeros((self.input_nodes,self.hidden_nodes))
self.weights_1_2_t = np.random.normal(0.0, self.output_nodes**-0.5,
(self.hidden_nodes, self.output_nodes))
print("Encrypting Weights...")
self.weights_0_1 = list()
for i,row in enumerate(self.weights_0_1_t):
sys.stdout.write("\rEncrypting Weights from Layer 0 to Layer 1:" + str(float((i+1) * 100) / len(self.weights_0_1_t))[0:4] + "% done")
self.weights_0_1.append(one_way_encrypt_vector(row,scaling_factor).astype('int64'))
print("")
self.weights_1_2 = list()
for i,row in enumerate(self.weights_1_2_t):
sys.stdout.write("\rEncrypting Weights from Layer 1 to Layer 2:" + str(float((i+1) * 100) / len(self.weights_1_2_t))[0:4] + "% done")
self.weights_1_2.append(one_way_encrypt_vector(row,scaling_factor).astype('int64'))
self.weights_1_2 = transpose(self.weights_1_2)
self.learning_rate = learning_rate
self.layer_0 = np.zeros((1,input_nodes))
self.layer_1 = np.zeros((1,hidden_nodes))
def sigmoid(self,x):
return 1 / (1 + np.exp(-x))
def sigmoid_output_2_derivative(self,output):
return output * (1 - output)
def update_input_layer(self,review):
# 清除之前的状态,重置层至全0
self.layer_0 *= 0
for word in review.split(" "):
self.layer_0[0][self.word2index[word]] = 1
def get_target_for_label(self,label):
if(label == 'POSITIVE'):
return 1
else:
return 0
def train(self, training_reviews_raw, training_labels):
training_reviews = list()
for review in training_reviews_raw:
indices = set()
for word in review.split(" "):
if(word in self.word2index.keys()):
indices.add(self.word2index[word])
training_reviews.append(list(indices))
layer_1 = np.zeros_like(self.weights_0_1[0])
start = time.time()
correct_so_far = 0
total_pred = 0.5
for i in range(len(training_reviews_raw)):
review_indices = training_reviews[i]
label = training_labels[i]
layer_1 *= 0
for index in review_indices:
layer_1 += self.weights_0_1[index]
layer_1 = layer_1 / float(len(review_indices))
layer_1 = layer_1.astype('int64') # 取整至最接近的整数
layer_2 = sigmoid(innerProd(layer_1,self.weights_1_2[0],M_onehot[len(layer_1) - 2][1],l) / float(scaling_factor))[0:2]
if(label == 'POSITIVE'):
layer_2_delta = layer_2 - (c_ones[len(layer_2) - 2] * scaling_factor)
else:
layer_2_delta = layer_2
weights_1_2_trans = transpose(self.weights_1_2)
layer_1_delta = mat_mul_forward(layer_2_delta,weights_1_2_trans,scaling_factor).astype('int64')
self.weights_1_2 -= np.array(outer_product(layer_2_delta,layer_1)) * self.learning_rate
for index in review_indices:
self.weights_0_1[index] -= (layer_1_delta * self.learning_rate).astype('int64')
# 我们将即时解密,以便查看发生了什么
total_pred += (s_decrypt(layer_2)[0] / scaling_factor)
if((s_decrypt(layer_2)[0] / scaling_factor) >= (total_pred / float(i+2)) and label == 'POSITIVE'):
correct_so_far += 1
if((s_decrypt(layer_2)[0] / scaling_factor) < (total_pred / float(i+2)) and label == 'NEGATIVE'):
correct_so_far += 1
reviews_per_second = i / float(time.time() - start)
sys.stdout.write("\rProgress:" + str(100 * i/float(len(training_reviews_raw)))[:4] + "% Speed(reviews/sec):" + str(reviews_per_second)[0:5] + " #Correct:" + str(correct_so_far) + " #Trained:" + str(i+1) + " Training Accuracy:" + str(correct_so_far * 100 / float(i+1))[:4] + "%")
if(i % 100 == 0):
print(i)
def test(self, testing_reviews, testing_labels):
correct = 0
start = time.time()
for i in range(len(testing_reviews)):
pred = self.run(testing_reviews[i])
if(pred == testing_labels[i]):
correct += 1
reviews_per_second = i / float(time.time() - start)
sys.stdout.write("\rProgress:" + str(100 * i/float(len(testing_reviews)))[:4] \
+ "% Speed(reviews/sec):" + str(reviews_per_second)[0:5] \
+ "% #Correct:" + str(correct) + " #Tested:" + str(i+1) + " Testing Accuracy:" + str(correct * 100 / float(i+1))[:4] + "%")
def run(self, review):
# 输入层
# 隐藏层
self.layer_1 *= 0
unique_indices = set()
for word in review.lower().split(" "):
if word in self.word2index.keys():
unique_indices.add(self.word2index[word])
for index in unique_indices:
self.layer_1 += self.weights_0_1[index]
# 输出层
layer_2 = self.sigmoid(self.layer_1.dot(self.weights_1_2))
if(layer_2[0] >= 0.5):
return "POSITIVE"
else:
return "NEGATIVE"
Progress:0.0% Speed(reviews/sec):0.0 #Correct:1 #Trained:1 Training Accuracy:100.%0
Progress:0.41% Speed(reviews/sec):1.978 #Correct:66 #Trained:101 Training Accuracy:65.3%100
Progress:0.83% Speed(reviews/sec):2.014 #Correct:131 #Trained:201 Training Accuracy:65.1%200
Progress:1.25% Speed(reviews/sec):2.011 #Correct:203 #Trained:301 Training Accuracy:67.4%300
Progress:1.66% Speed(reviews/sec):2.003 #Correct:276 #Trained:401 Training Accuracy:68.8%400
Progress:2.08% Speed(reviews/sec):2.007 #Correct:348 #Trained:501 Training Accuracy:69.4%500
Progress:2.5% Speed(reviews/sec):2.015 #Correct:420 #Trained:601 Training Accuracy:69.8%600
Progress:2.91% Speed(reviews/sec):1.974 #Correct:497 #Trained:701 Training Accuracy:70.8%700
Progress:3.33% Speed(reviews/sec):1.973 #Correct:581 #Trained:801 Training Accuracy:72.5%800
Progress:3.75% Speed(reviews/sec):1.976 #Correct:666 #Trained:901 Training Accuracy:73.9%900
Progress:4.16% Speed(reviews/sec):1.983 #Correct:751 #Trained:1001 Training Accuracy:75.0%1000
Progress:4.33% Speed(reviews/sec):1.940 #Correct:788 #Trained:1042 Training Accuracy:75.6%
....
十、相比数据加密的优势
和这一做法最相似的是加密训练数据,然后在加密数据上训练神经网络(接受加密输入并预测加密输出)。这是一个出色的想法。然而,其实它有一些缺陷。首先也是最重要的,加密数据意味着对任何不具有加密数据的私钥的人而言,该神经网络完全无用。这样就不可能在不同的私有数据源上训练同一深度学习模型了。大部分商业应用有这样的需求,需要汇总消费者的数据。理论上,我们本来想要让每个消费者用他们自己的密钥保护自己的数据,然而同态加密数据要求所有人使用相同的钥。
而加密网络则没有这个限制。
基于上述方法,你可以训练一个平常的、解密的神经网络一段时间,加密它,将它和相应的公钥发给A方(A方可以基于其所有的数据训练网络一段时间……A方保留数据)。接着,你可以收回这个网络,解密它,用另一个钥加密网络,然后发给B方,B方在其所有的数据上进行一些训练。由于网络自身被加密了,你可以完全控制全过程中你刻画的智能。A方和B方将无法知道他们各自收到的是同一个网络,也无法知道之前见过这个网络,或在自己的数据上用过这个网络。你的公司保留对神经网络中的知识产权的控制,而每个用户保留对他们自己的数据的控制。
十一、以后的工作
存在更快、更安全的同态加密算法。我相信将本项工作移植到YASHE会是一个正确的方向。由于一些系统复杂性,也许开发一个能让用户更简单地进行加密的框架会是一个好主意。一般而言,为了达到生产环境要求的质量,HE需要变得更快。然而,这方面的进展十分迅速。我确信我们会在不久的将来达到这一点。
十二、潜在应用
分布式AI 商业公司可以分布式地部署它们的模型(用于训练或使用),而无需冒智能被窃的风险。
保护消费者隐私 之前的应用提供了这样的可能性:消费者保留他们的数据,选择不同的模型在自己的设备上训练,不用将数据发送到别处。如果商业公司的智能在分布式场景中没有被窃的风险,那么他们不尊重消费者隐私的借口就会少很多。数据就是力量,它需要回归到人们手中。
受控超智能 网络可以充分发展其智能,不过除非它具有密钥,否则它只能预测乱码。
原文地址:http://iamtrask.github.io/2017/03/17/safe-ai/