旅行销售员的演化：基于Python实现遗传算法

2018 年 8 月 5 日 论智

来源：Medium

编译：weakish

编者按：麦肯锡顾问Eric Stoltz以旅行推销员问题为例，简明地介绍了遗传算法的原理及Python实现。

借鉴自然选择的灵感，遗传算法（GA）是一种迷人的求解搜索和优化问题方法。尽管已经有很多关于GA的文章，这些文章很少演示如何一步一步地使用Python实现GA算法，解决一个比较复杂的问题。所以我写了这篇教程！读完这篇教程后，你将对如何从头实现GA算法有一个完整的了解。

导言

问题

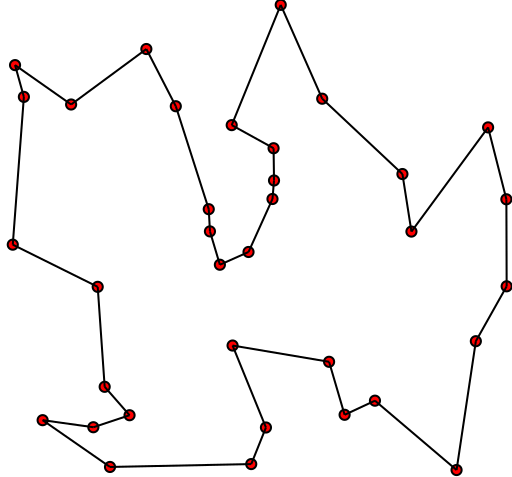
这篇教程将使用GA求解旅行推销员问题（TSP）：

给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短路由。

TSP示意图（作者：Xypron；许可：公有领域）

记住两条重要的规则：

每座城市仅访问一次（不重不漏）
必须返回起始城市

方法

让我们从一些定义开始：

基因（gene）：一座城市（以(x, y)坐标表示）
个体（individual）或染色体（chromosome）：满足以上条件的一个路由
种群（population）：一组可能的路由（即，一组个体）
父母（parents）：两个路由相组合，创建一个新路由
交配池（mating pool）：一组父母，用来创建下一代种群（即创建下一代路由）
适应度（fitness）：一个告诉我们每个路由有多好的函数（在我们的例子中，也就是距离多短）
突变（mutation）：在种群中引入变化的方法，随机交换路由中的两个城市
精英选择（Elitism）：将最好的个体保留至下一代

GA算法的进行过程如下：

创建种群
确定适应度
选择交配池
繁殖
变异
重复

现在，让我们来动手实现。

创建我们的遗传算法

导入一些机器学习的标准包：

  
  
    
   
   
     import numpy as np
   
   
     import random
   
   
     import operator
   
   
     import pandas as pd
   
   
     import matplotlib.pyplot as plt

创建城市和适应度类

我们首先创建City（城市）类，城市不过是(x, y)坐标。City类中包含distance函数（根据勾股定理计算一对城市间的距离）。

  
  
    
   
   
     class City:
   
   
         def __init__(self, x, y):
   
   
             self.x = x
   
   
             self.y = y
   
   
     
   
   
         def distance(self, city):
   
   
             xDis = abs(self.x - city.x)
   
   
             yDis = abs(self.y - city.y)
   
   
             distance = np.sqrt((xDis ** 2) + (yDis ** 2))
   
   
             return distance
   
   
     
   
   
         def __repr__(self):
   
   
             return "(" + str(self.x) + "," + str(self.y) + ")"

在Fitness（适应度）类中，我们将适应度（routeFitness）定义为路由距离（routeDistance）的倒数。我们想要最小化路由距离，因此较大的适应度较优。注意routeDistance的定义考虑到了我们需要回到起点。

  
  
    
   
   
     class Fitness:
   
   
         def __init__(self, route):
   
   
             self.route = route
   
   
             self.distance = 0
   
   
             self.fitness= 0.0
   
   
     
   
   
         def routeDistance(self):
   
   
             if self.distance ==0:
   
   
                 pathDistance = 0
   
   
                 for i in range(0, len(self.route)):
   
   
                     fromCity = self.route[i]
   
   
                     toCity = None
   
   
                     if i + 1 < len(self.route):
   
   
                         toCity = self.route[i + 1]
   
   
                     else:
   
   
                         toCity = self.route[0]
   
   
                     pathDistance += fromCity.distance(toCity)
   
   
                 self.distance = pathDistance
   
   
             return self.distance
   
   
     
   
   
         def routeFitness(self):
   
   
             if self.fitness == 0:
   
   
                 self.fitness = 1 / float(self.routeDistance())
   
   
             return self.fitness

创建种群

现在我们将生产初始种群（第一代）。我们需要一个能够生成满足条件的路由的函数（我们将在教程末尾创建城市列表）。我们通过随机选择访问城市的顺序创建一个个体：

  
  
    
   
   
     def createRoute(cityList):
   
   
         route = random.sample(cityList, len(cityList))
   
   
         return route

重复运行createRoute函数，直到我们有了足够的个体：

  
  
    
   
   
     def initialPopulation(popSize, cityList):
   
   
         population = []
   
   
     
   
   
         for i in range(0, popSize):
   
   
             population.append(createRoute(cityList))
   
   
         return population

确定适应度

接下来到了有意思的演化部分。为了模拟“适者生存”，我们利用Fitness排序种群中的每个个体。我们的输出是一个有序列表，包括路由ID和相应的适应度分数。

  
  
    
   
   
     def rankRoutes(population):
   
   
         fitnessResults = {}
   
   
         for i in range(0,len(population)):
   
   
             fitnessResults[i] = Fitness(population[i]).routeFitness()
   
   
         return sorted(fitnessResults.items(), key = operator.itemgetter(1), reverse = True)

选择交配池

选择用来产生下一代的父母有若干种方法。其中最常见的两种是适应度比例选择（fitness proportionate selection）和锦标赛选择（tournament selection）。适应度比例选择又称为轮盘赌选择（roulette wheel selection）。

适应度比例选择 （下面实现的版本）：基于每个个体相对于种群的适应度分配选中的概率。可以看成适应度加权选择概率。
锦标赛选择：从种群中随机选择一些个体，其中适应度最高的被选为父母的一方。重复这一过程选出父母的另一方。

另外也可以考虑精英选择。种群中表现最优的个体自动进入下一代，确保留存最成功的个体。

为清晰计，我们将分两步（selection、matingPool）创建交配池。在selection函数中，我们将根据rankRoutes的输出判定选择哪些路由。我们为每个个体计算相对适应度权重（创建轮盘），然后将这些权重与一个随机数比较，以选择交配池。同时，我们打算保留最佳的路由，因此引入了精英选择。最后，selection函数返回路由ID的列表，供matingPool函数使用。

  
  
    
   
   
     def selection(popRanked, eliteSize):
   
   
         selectionResults = []
   
   
         df = pd.DataFrame(np.array(popRanked), columns=["Index","Fitness"])
   
   
         df['cum_sum'] = df.Fitness.cumsum()
   
   
         df['cum_perc'] = 100*df.cum_sum/df.Fitness.sum()
   
   
     
   
   
         for i in range(0, eliteSize):
   
   
             selectionResults.append(popRanked[i][0])
   
   
         for i in range(0, len(popRanked) - eliteSize):
   
   
             pick = 100*random.random()
   
   
             for i in range(0, len(popRanked)):
   
   
                 if pick <= df.iat[i,3]:
   
   
                     selectionResults.append(popRanked[i][0])
   
   
                     break
   
   
         return selectionResults

有了selection提供的路由ID，我们可以创建交配池了。

  
  
    
   
   
     def matingPool(population, selectionResults):
   
   
         matingpool = []
   
   
         for i in range(0, len(selectionResults)):
   
   
             index = selectionResults[i]
   
   
             matingpool.append(population[index])
   
   
         return matingpool

繁殖

创建好了交配池后，我们可以通过交叉（crossover）过程生产下一代。例如，假设个体是由0和1组成的字符串，我们可以直接选定一个交叉点，铰接两个字符串以产生后代。

然而，TSP要求每个位置出现且仅出现一次。为了遵循这条规则，我们将使用一种特殊的繁殖函数有序交叉（ordered crossover）。在有序交叉中，我们随机选择父字符串的一个子集，然后用母字符串中的基因填充路由的剩余空位。填充时，按照基因在母字符串中出现的次序依次填充，跳过选中的父字符串子集中已有的基因。

有序交叉示意图（来源：Lee Jacobson）

  
  
    
   
   
     def breed(parent1, parent2):
   
   
         child = []
   
   
         childP1 = []
   
   
         childP2 = []
   
   
     
   
   
         geneA = int(random.random() * len(parent1))
   
   
         geneB = int(random.random() * len(parent1))
   
   
     
   
   
         startGene = min(geneA, geneB)
   
   
         endGene = max(geneA, geneB)
   
   
     
   
   
         for i in range(startGene, endGene):
   
   
             childP1.append(parent1[i])
   
   
     
   
   
         childP2 = [item for item in parent2 if item not in childP1]
   
   
     
   
   
         child = childP1 + childP2
   
   
         return child

在整个交配池上进行交叉操作（注意我们附加了精英选择）：

  
  
    
   
   
     def breedPopulation(matingpool, eliteSize):
   
   
         children = []
   
   
         length = len(matingpool) - eliteSize
   
   
         pool = random.sample(matingpool, len(matingpool))
   
   
     
   
   
         for i in range(0,eliteSize):
   
   
             children.append(matingpool[i])
   
   
     
   
   
         for i in range(0, length):
   
   
             child = breed(pool[i], pool[len(matingpool)-i-1])
   
   
             children.append(child)
   
   
         return children

变异

变异在GA中起到了重要作用，它通过引入新路由让我们得以探索解答空间的其他部分，避免收敛到局部最优值。和交叉类似，TSP问题中的变异需要特殊考虑。同样，如果我们的染色体由0和1组成，变异不过是给基因分配一个较低的由0变为1（或由1变0）的概率。

然而，因为我们需要遵守TSP的规则，我们无法丢弃城市。我们将转而使用交换变异（swap mutation）。这意味着，我们指定一个较低的概率，两座城市会在我们的路由中交换位置。

  
  
    
   
   
     def mutate(individual, mutationRate):
   
   
         for swapped in range(len(individual)):
   
   
             if(random.random() < mutationRate):
   
   
                 swapWith = int(random.random() * len(individual))
   
   
     
   
   
                 city1 = individual[swapped]
   
   
                 city2 = individual[swapWith]
   
   
     
   
   
                 individual[swapped] = city2
   
   
                 individual[swapWith] = city1
   
   
         return individual

在整个种群上应用mutate函数：

  
  
    
   
   
     def mutatePopulation(population, mutationRate):
   
   
         mutatedPop = []
   
   
     
   
   
         for ind in range(0, len(population)):
   
   
             mutatedInd = mutate(population[ind], mutationRate)
   
   
             mutatedPop.append(mutatedInd)
   
   
         return mutatedPop

重复

基本上差不多了。现在让我们把以上部分整合起来，创建一个产生下一代的函数。首先，我们计算当前种群的适应度。接着，我们选择潜在的父母，以创建交配池。最后，我们生产（交叉、变异）下一代。

  
  
    
   
   
     def nextGeneration(currentGen, eliteSize, mutationRate):
   
   
         popRanked = rankRoutes(currentGen)
   
   
         selectionResults = selection(popRanked, eliteSize)
   
   
         matingpool = matingPool(currentGen, selectionResults)
   
   
         children = breedPopulation(matingpool, eliteSize)
   
   
         nextGeneration = mutatePopulation(children, mutationRate)
   
   
         return nextGeneration

演化

我们已经具备了GA所需的一切！现在我们只需创建一个初始种群，然后就可以不断演化了。按照我们设定的代数演化后，将返回最佳路由。另外，我们将打印初始的路由距离，最终的路由距离，来看看我们提升了多少。

  
  
    
   
   
     def geneticAlgorithm(population, popSize, eliteSize, mutationRate, generations):
   
   
         pop = initialPopulation(popSize, population)
   
   
         print("Initial distance: " + str(1 / rankRoutes(pop)[0][1]))
   
   
     
   
   
         for i in range(0, generations):
   
   
             pop = nextGeneration(pop, eliteSize, mutationRate)
   
   
     
   
   
         print("Final distance: " + str(1 / rankRoutes(pop)[0][1]))
   
   
         bestRouteIndex = rankRoutes(pop)[0][0]
   
   
         bestRoute = pop[bestRouteIndex]
   
   
         return bestRoute

运行演化算法

万事俱备，只欠东风。我们现在只需要创建经过的城市列表。这里，我们将随机创建25座城市来演示GA算法：

  
  
    
   
   
     cityList = []
   
   
     
   
   
     for i in range(0,25):
   
   
         cityList.append(City(x=int(random.random() * 200), y=int(random.random() * 200)))

只需一行代码即可运行演化算法。接下来艺术和科学的交汇之处：判断哪些假定效果最好。这里，我们将选择如下参数：每代100个个体，保留20个精英个体，给定基因的变异率为1%，运行500代：

  
  
    
   
   
     geneticAlgorithm(population=cityList, popSize=100, eliteSize=20, mutationRate=0.01, generations=500)

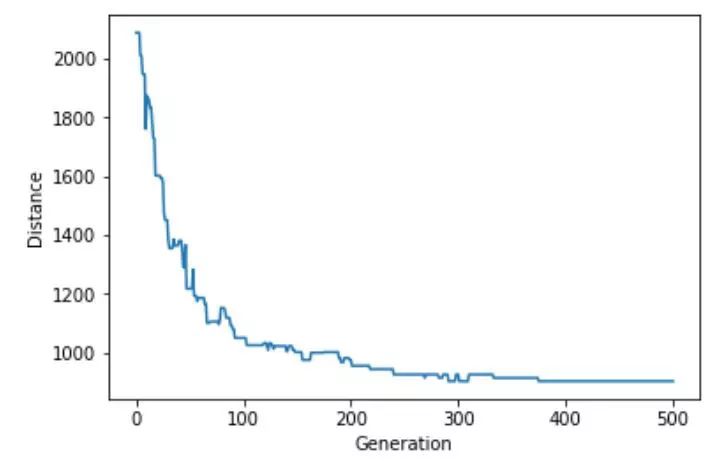
附加题: 绘制趋势

我们希望能查看距离随时间缩短的趋势，因此对geneticAlgorithm函数进行了一项小小的改动，保存每代的最短距离，并据此绘制图形。

  
  
    
   
   
     def geneticAlgorithmPlot(population, popSize, eliteSize, mutationRate, generations):
   
   
         pop = initialPopulation(popSize, population)
   
   
         progress = []
   
   
         progress.append(1 / rankRoutes(pop)[0][1])
   
   
     
   
   
         for i in range(0, generations):
   
   
             pop = nextGeneration(pop, eliteSize, mutationRate)
   
   
             progress.append(1 / rankRoutes(pop)[0][1])
   
   
     
   
   
         plt.plot(progress)
   
   
         plt.ylabel('Distance')
   
   
         plt.xlabel('Generation')
   
   
         plt.show()

结语

我希望这样亲手学习如何创建自己的GA算法是一个有意思的过程。请自行尝试，看看你可以得到多短的路由。或者进一步尝试在其他问题上实现GA；想象你将如何修改bred和mutate函数来处理其他类型的染色体。我们这里只涉及一些皮毛！

本文配套的Jupyter Notebook见GitHub：ezstoltz/genetic-algorithm/geneticalgorithmTSP.ipynb

参考链接

http://www.theprojectspot.com/tutorial-post/applying-a-genetic-algorithm-to-the-travelling-salesman-problem/5
https://gist.github.com/turbofart/3428880
https://gist.github.com/NicolleLouis/d4f88d5bd566298d4279bcb69934f51d
https://en.wikipedia.org/wiki/Travelling_salesman_problem

原文地址：https://towardsdatascience.com/evolution-of-a-salesman-a-complete-genetic-algorithm-tutorial-for-python-6fe5d2b3ca35