《多模态大语言模型时代的数学推理研究：基准、方法与挑战》

摘要

数学推理作为人类认知的核心方面，在许多领域中至关重要，从教育问题解决到科学进展都离不开它。随着人工通用智能（AGI）的发展，将大语言模型（LLMs）与数学推理任务相结合变得愈发重要。本研究是对多模态大语言模型（MLLMs）时代数学推理的首次全面分析。我们回顾了自2021年以来发布的200多篇相关研究，重点分析了数学-大语言模型（Math-LLMs）领域的最新进展，特别是在多模态设置下的应用。我们将该领域划分为三个维度：基准、方法论和挑战。特别地，我们探讨了多模态数学推理流程，及其中文化的（M）LLMs和相关方法论的角色。最后，我们识别出五个主要挑战，这些挑战阻碍了该领域AGI的实现，并为提升多模态推理能力提供了见解。本综述为研究界提供了重要资源，助力大语言模型在处理复杂多模态推理任务时的能力提升。

1 引言

数学推理是人类认知能力的关键方面，涉及通过逻辑和系统化思维从一组前提推导结论的过程（Jonsson et al., 2022；Yu et al., 2024b）。它在许多应用领域中发挥着重要作用，从教育中的问题解决到科学发现的突破。随着人工通用智能（AGI）的不断发展（Zhong et al., 2024），将大语言模型（LLMs）与数学推理任务相结合变得愈加重要。这些模型在语言理解方面具有卓越的能力，能够模拟曾被认为是人类特有的复杂推理过程。近年来，学术界和工业界都日益关注这一方向（Wang et al., 2024d；Xu et al., 2024a；Lu et al., 2022b）。

数学推理任务的输入是多样化的，不仅限于传统的文本输入，还扩展到多模态设置，如图1所示。数学问题通常不仅涉及文本信息，还包括视觉元素，如图表、图形或方程式，它们为解决问题提供了必要的背景（Wang et al., 2024e；Yin et al., 2024）。在过去的一年中，多模态数学推理已成为多模态大语言模型（MLLMs）的研究重点（Zhang et al., 2024c；Bai et al., 2024；Wu et al., 2023a）。这一转变源于认识到，像数学这样的推理任务需要能够同时整合和处理多种模态的模型，才能实现类似人类的推理表现。然而，多模态数学推理面临着显著的挑战，包括不同模态之间的复杂交互、对深层语义理解的需求，以及跨模态背景信息保持的重要性（Liang et al., 2024a；Song et al., 2023；Fu et al., 2024b）。这些挑战是实现AGI的核心问题，模型必须能够无缝地整合多种知识形式，执行复杂的推理任务。

Math-LLM进展

图2展示了自2021年以来，随着LLM的快速发展，数学特定的大语言模型（Math-LLMs）数量稳步增长，并且支持多语言和多模态能力的水平也有所提升（更多细节见附录A）。这一领域的标志性进展包括GPT-f（Polu和Sutskever，2021）和Minerva（Lewkowycz等，2022）的推出，以及Hypertree Proof Search（Lample等，2022）和Jiuzhang 1.0（Zhao等，2022），前者突出了定理证明能力的进展，后者则展示了数学问题理解的提升。2023年，随着SkyworkMath（Zeng等，2024）等模型的推出，出现了多样化和专业化的趋势，并且增强了多模态支持。在2024年，数学指导（如Qwen2.5-Math（Yang等，2024a））和证明（如DeepSeek-Proof（Xin等，2024a））能力得到了显著提升。此外，本年度还涌现出一些带有视觉组件的Math-LLM，如MathGLM-Vision（Yang等，2024b）。

研究范围

以往的综述未能全面捕捉到多模态大语言模型时代数学推理的进展与挑战。如表1所示，一些研究集中于深度学习技术在数学推理中的应用（Lu et al., 2022b）或特定领域，如定理证明（Li et al., 2024f），但忽视了LLM崛起所带来的快速进展。另一些则扩展了范围，讨论了LLM在教育（Wang et al., 2024d；Xu et al., 2024a；Li et al., 2023a）或数学领域（Ahn et al., 2024；Liu et al., 2023b）中的作用，但未深入探讨多模态设置下数学推理的发展和挑战。因此，本综述旨在填补这一空白，首次全面分析多模态大语言模型时代数学推理的现状，重点关注三个关键维度：基准、方法论和挑战。

结构

本文回顾了自2021年以来，AI领域关于基于（M）LLM的数学推理的200多篇相关文献，并总结了Math-LLM的进展。我们首先从基准的角度分析该领域，讨论LLM-based数学推理任务的三个关键方面：数据集、任务和评估（第2节）。接下来，我们探讨（M）LLM在数学推理中的作用，并将其分类为推理者、增强者和规划者（第3节）。最后，我们识别出多模态大语言模型时代数学推理面临的五大核心挑战（第4节）。本综述旨在为学术界提供全面的见解，推动LLM在处理复杂多模态推理任务方面的能力提升。

基准测试在数学推理中的作用

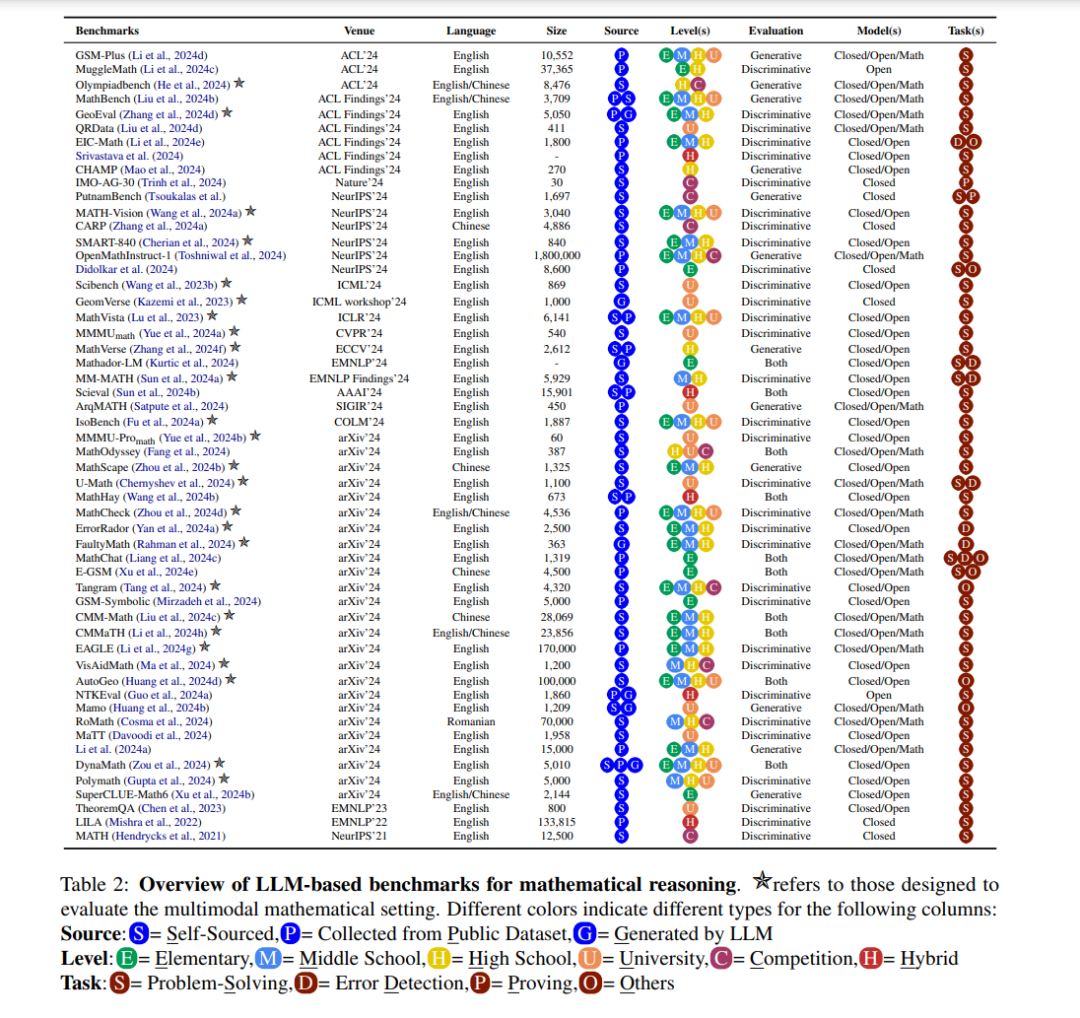
基准测试在推动大语言模型（LLM）研究方面发挥着至关重要的作用，因为它为评估推理任务的表现提供了标准化、可复现的流程。虽然像GSM8K（Cobbe et al., 2021）和MathQA（Amini et al., 2019）这样的先前基准在LLM出现之前发挥了重要作用，但我们关注的重点是与（M）LLM相关的基准。在本节中，我们将对近年来在（M）LLM背景下的数学推理基准进行全面分析（见表2）。本节分为三个子节：数据集（第2.2节）、任务（第2.3节）和评估（第2.4节）。

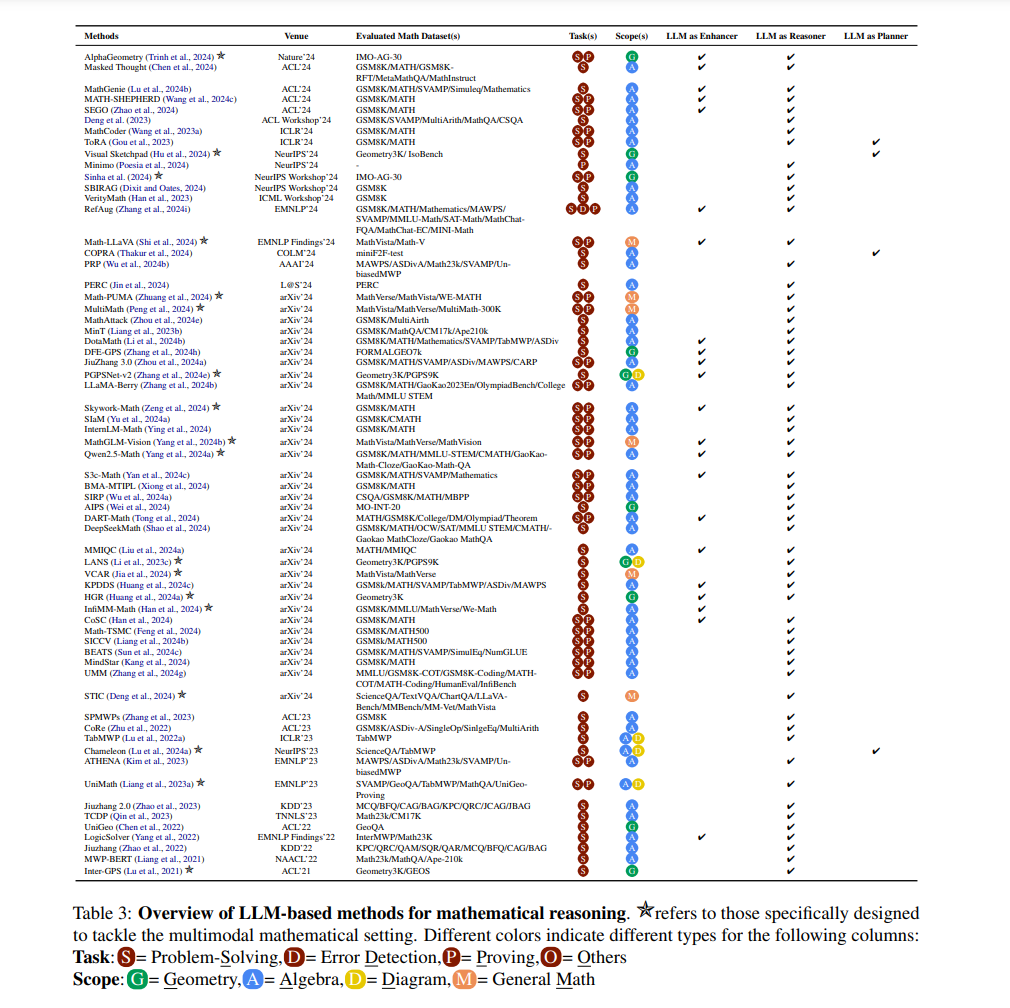
**方法论视角 **概述与发现 多模态大语言模型（MLLMs）已被应用于多种方式，以解决广泛的数学推理任务。根据我们对近期方法论的全面回顾（总结见表3），我们将相关研究分类为三种不同的范式：LLM作为推理者（第3.2节）、LLM作为增强者（第3.3节）和LLM作为规划者（第3.4节）。

研究发现 首先，当前以方法为导向的研究主要集中在单一模态设置上，大多数研究仅关注代数任务。然而，自2024年以来，越来越多的多模态方法被引入，将数学推理的范围扩展到几何、图形，甚至更广泛的数学概念。这一转变标志着通过多模态学习增强模型鲁棒性的兴趣日益增长，因为它能够应对数学问题的多样性。其次，关于评估任务，问题求解和定理证明正逐渐成为研究的重点，而部分研究也集中在错误检测或其他任务上（例如，RefAug将错误修正和后续问答作为评估任务（Zhang et al., 2024i））。最后，关于LLM的角色，推理者（Reasoner）是最常见的角色，其次是增强者（Enhancer），而规划者（Planner）仍然是较少研究的领域，但由于多智能体智能的最新进展，它具有很大的潜力。

**结论

**在本综述中，我们全面回顾了多模态大语言模型（MLLMs）背景下数学推理的进展与挑战。我们强调了Math-LLMs发展的重要进展，以及多模态集成在解决复杂推理任务中的日益重要性。我们识别出了五个关键挑战，这些挑战对继续发展能够执行复杂数学推理任务的AGI系统至关重要。随着研究的持续推进，解决这些挑战对于释放LLM在多模态设置中的全部潜力至关重要。我们希望本综述为未来的LLM研究提供有价值的见解，最终推动AI系统在数学推理方面达到更高的效能和更接近人类的能力。