自动化所首篇「深度图结构学习鲁棒表示」简明综述论文

摘要

图神经网络(GNNs)广泛应用于分析图结构数据。大多数GNN方法对图结构的质量非常敏感，通常需要一个完美的图结构来学习信息嵌入。

然而，图中噪声的普遍性需要学习鲁棒表示以解决真实世界问题。为了提高GNN模型的鲁棒性，许多研究围绕图结构学习(Graph Structure Learning, GSL)这一中心概念提出，旨在共同学习优化的图结构及其表示。

为此，在本研究中，我们广泛回顾了学习鲁棒表示的GSL方法的最新进展。具体来说，我们首先制定一个通用的GSL范式，然后回顾最先进的方法，根据它们如何建模图结构进行分类，然后是在其他图任务中包含GSL思想的应用。最后，我们指出了目前研究中存在的一些问题，并对未来的研究方向进行了讨论。

引言

图在表示对象及其复杂的交互时是普遍存在的。作为一种分析图形结构数据的强大工具，图神经网络(GNNs)已被广泛应用于各种领域的图分析任务，包括节点分类[Kipf and Welling, 2017], 链接预测 [Kipf and Welling, 2016; Zhang and Chen, 2018], 推荐 [Wu et al., 2019; Yu et al., 2020b; He et al., 2020], 信息检索 [Zhang et al., 2021; Yu et al., 2021]，等。

众所周知，深度神经网络容易受到噪声的干扰[Szegedy et al.， 2014]; 噪声甚至加剧了深度GNN模型所产生的表示质量，这对将GNN应用于现实世界的问题，特别是在一些风险高危的场景中，例如医学分析，提出了巨大的挑战。由于GNN通过递归聚合邻区信息来计算节点嵌入，这种迭代机制具有级联效应——图中的小噪声将传播到邻区节点，影响许多其他节点的嵌入。以社交网络为例，节点对应用户，边表示朋友关系。欺诈账户与真实账户建立虚假链接，很容易向整个网络注入错误信息，导致难以估算账户的可信性。此外，最近的研究表明，不被注意到的、故意的干扰(又称“干扰”)。在图结构中，容易导致错误的预测[Dai et al.， 2018;Zhu et al.， 2019;Zhang and Zitnik, 2020。因此，GNN对给定数据的质量高度敏感，通常需要一个完美的图结构来学习信息表示[Luo et al.， 2021]。

提高GNN模型的鲁棒性的一个主要关注点是为学习表示产生去噪的图结构[Jin等人，2020]。最近，大量的文献围绕着图结构学习(Graph Structure Learning, GSL)这一中心主题兴起，其目标是共同学习优化的图结构和相应的表示[Yu et .， 2020a]。不幸的是，许多GSL技术在不同的研究团体中被提出，它们从未被系统地调研过。为了在不同的研究之间建立联系并便于理解，在本文中，我们对用于鲁棒表示的深度GSL的最新工作进行了综述。具体来说，我们制定了一个通用的GSL范式，根据他们对图结构建模的方式对现有的工作进行分类，并突出每个模型的关键优点。此外，由于GSL在其他方面使GNN受益，我们将讨论在其他领域(如可解释性和图池化)合并GSL思想的应用。据我们所知，这是第一个全面回顾GSL研究最新进展的研究。

本综述的其余部分的结构如下。在第2节中，我们将介绍有关图结构学习的初步知识，并提出描述不同研究的一般范式。接下来，在第3节中，我们将现有的工作分为三个类别，并仔细检查每个类别中的代表性工作。第4节将进一步讨论在其他领域中包含GSL思想的应用程序。最后，我们在第5节中指出了现有工作中存在的一些挑战和一些潜在的研究方向，并在第6节对全文进行了总结。

结构学习的一般范式

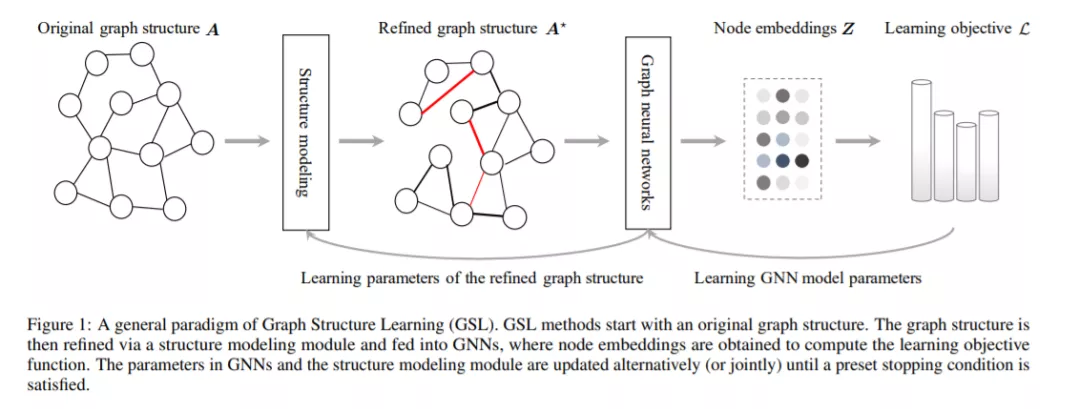
大多数现有的深度GSL工作都可以看作是在学习图形表示的现成GNN模型之上的插件模块。我们用一个通用范式来描述以前的研究，该范式包含三个组成部分: 结构建模、消息传播和学习目标。

结构建模。GSL的核心是一个编码函数，它对最优图结构A*用边权值表示。编码函数可以通过两两距离或可学习参数来定义边缘权值。在本研究中，我们将现有的研究分为以下三组:

• 度量学习方法，其中边权值来自于对表示之间的度量函数的学习

• 概率建模方法，假定图形是通过从某些分布的采样过程生成的，并使用可学习的参数对采样边缘的概率建模。

• 直接优化方法，在原始邻接矩阵的基础上，结合各种图的先验，对图结构进行细化。

消息传播。得到优化后的图结构A*，节点特征将传播到改进的领域。使用GNN模型，每个节点聚合来自邻近节点的信息，并产生一个嵌入Z*= f（A*，X），值得指出的是，由于对图结构进行优化的难度较大，很多方法采用迭代的方式进行结构建模和消息传播，直到满足几个停止条件。

学习目标。为了训练模型与改进的图结构，现有的工作通常定义了一个学习目标包含两个部分: L = L_task(Z ，Y）+ λL_reg(A，A），第一项Ltask是针对ground truth Y的任务特定目标，如用于节点分类的交叉熵和用于链路预测的贝叶斯个性化排名损失。第二项Lreg对学习到的图结构进行正则化，以满足一些先验拓扑约束，如稀疏性和低秩性。λ∈R是一个平衡这两项的超参数。