The Tight Bound for Pure Price of Anarchy in an Extended Miner's Dilemma Game

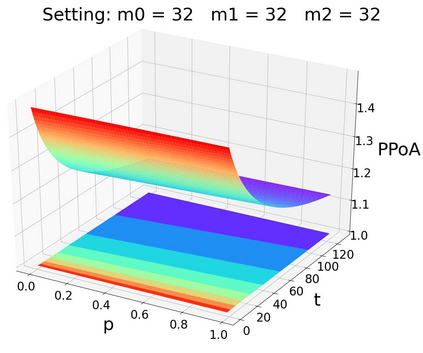
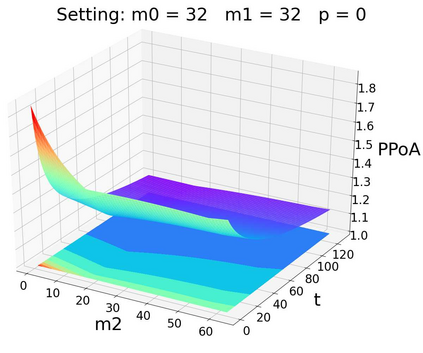
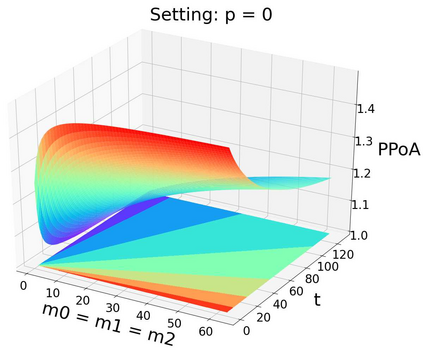
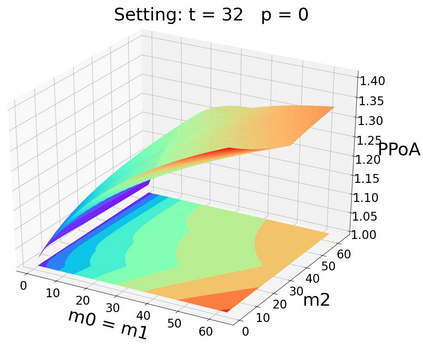
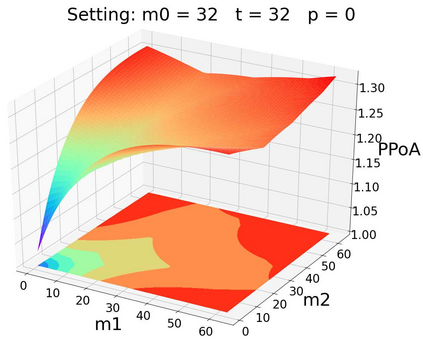
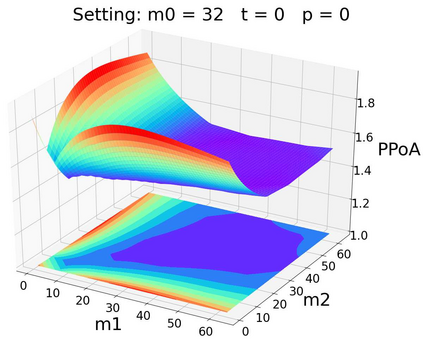
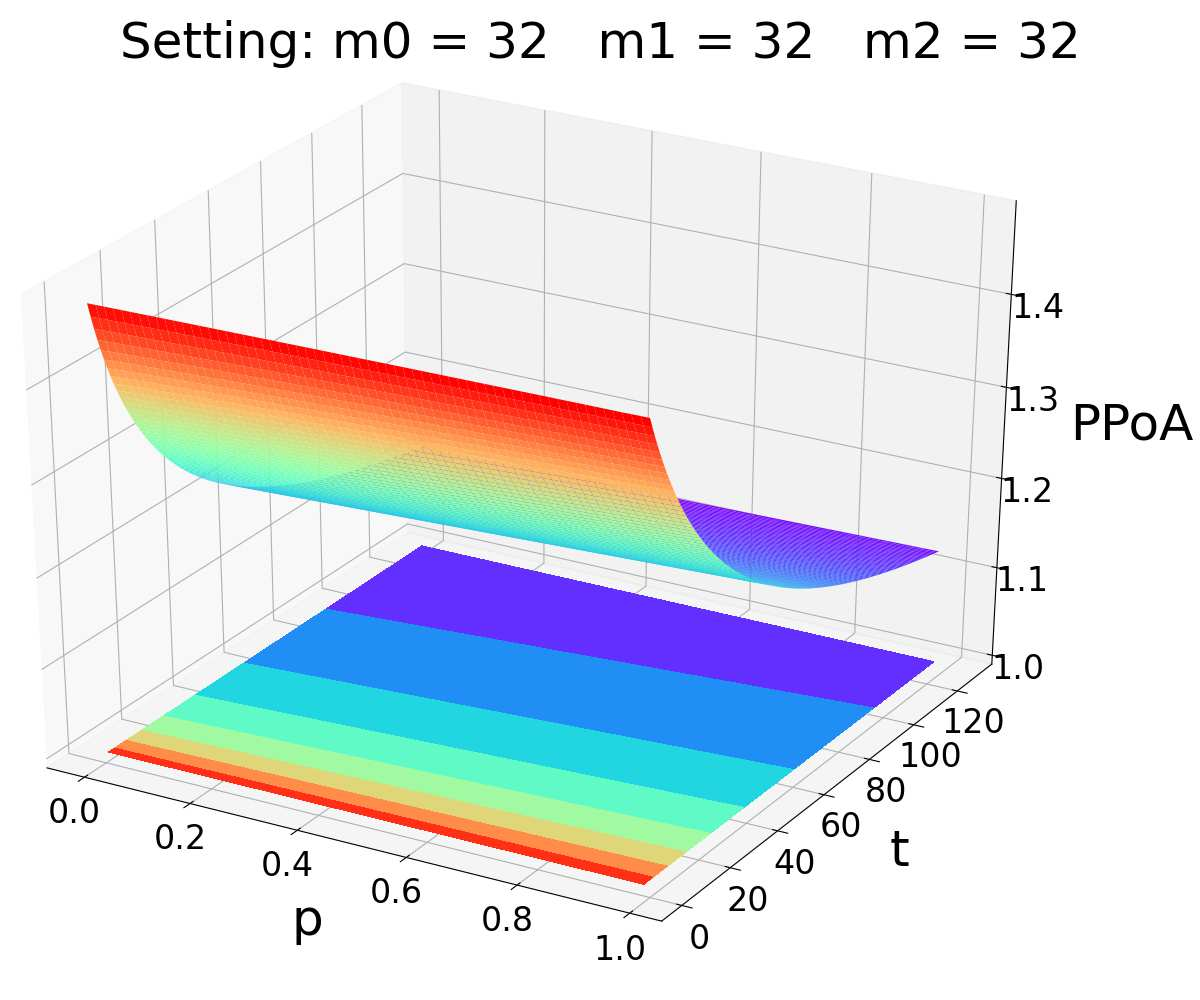
Pool block withholding attack is performed among mining pools in digital cryptocurrencies, such as Bitcoin. Instead of mining honestly, pools can be incentivized to infiltrate their own miners into other pools. These infiltrators report partial solutions but withhold full solutions, share block rewards but make no contribution to block mining. The block withholding attack among mining pools can be modeled as a non-cooperative game called "the miner's dilemm", which reduces effective mining power in the system and leads to potential systemic instability in the blockchain. However, existing literature on the game-theoretic properties of this attack only gives a preliminary analysis, e.g., an upper bound of 3 for the pure price of anarchy (PPoA) in this game, with two pools involved and no miner betraying. Pure price of anarchy is a measurement of how much mining power is wasted in the miner's dilemma game. Further tightening its upper bound will bring us more insight into the structure of this game, so as to design mechanisms to reduce the systemic loss caused by mutual attacks. In this paper, we give a tight bound of (1, 2] for the pure price of anarchy. Moreover, we show the tight bound holds in a more general setting, in which infiltrators may betray.We also prove the existence and uniqueness of pure Nash equilibrium in this setting. Inspired by experiments on the game among three mining pools, we conjecture that similar results hold in the N-player miner's dilemma game (N>=2).