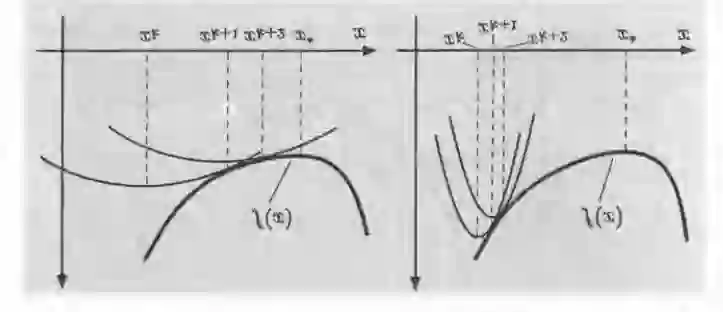
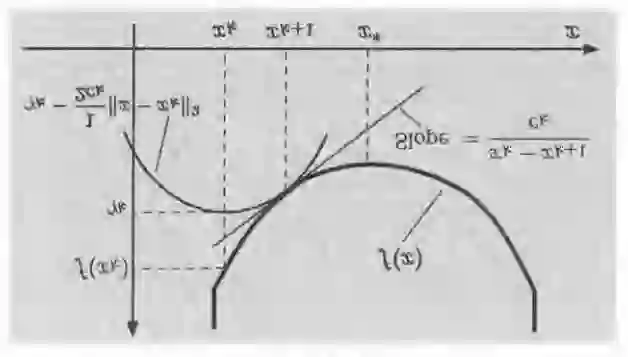
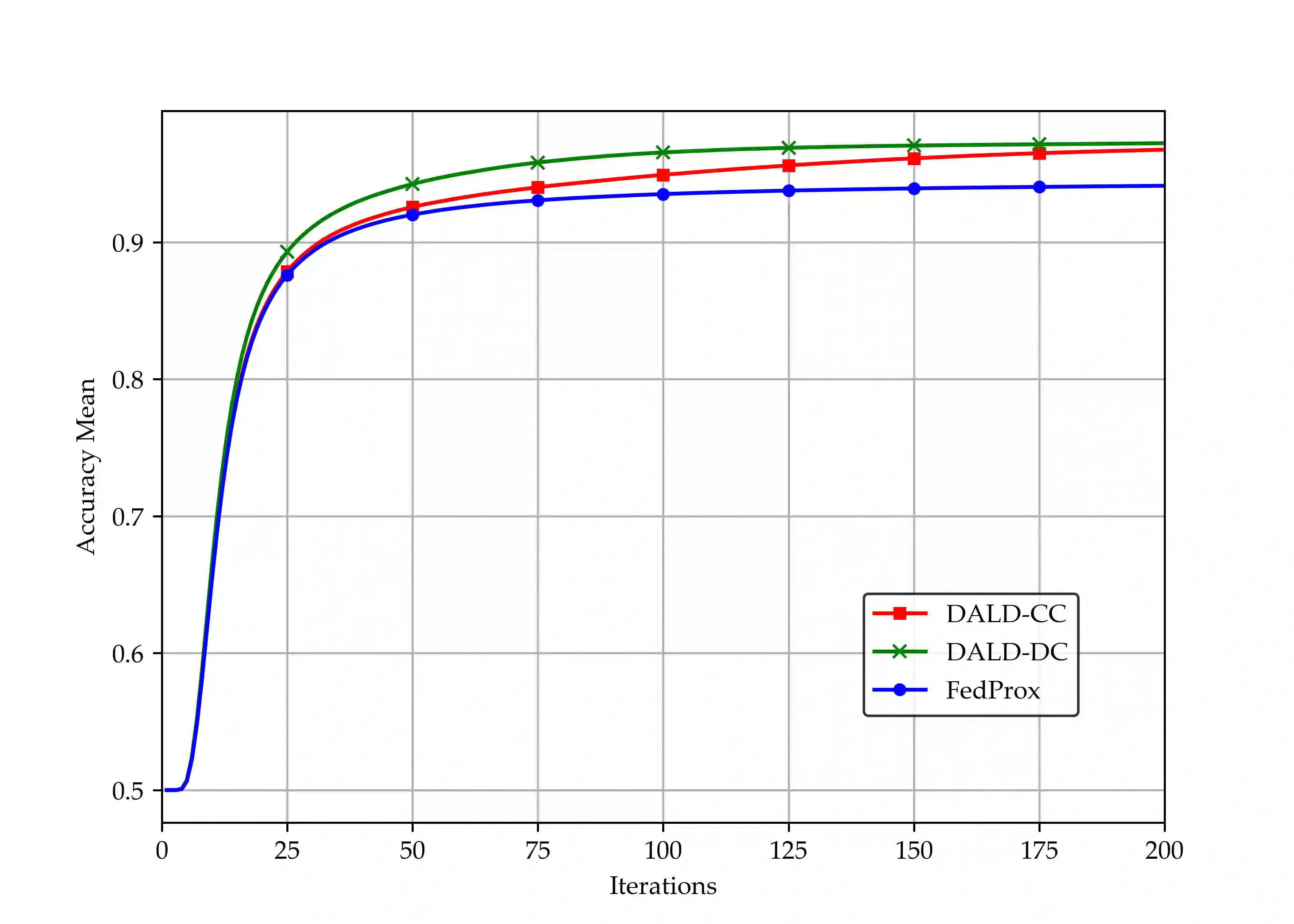
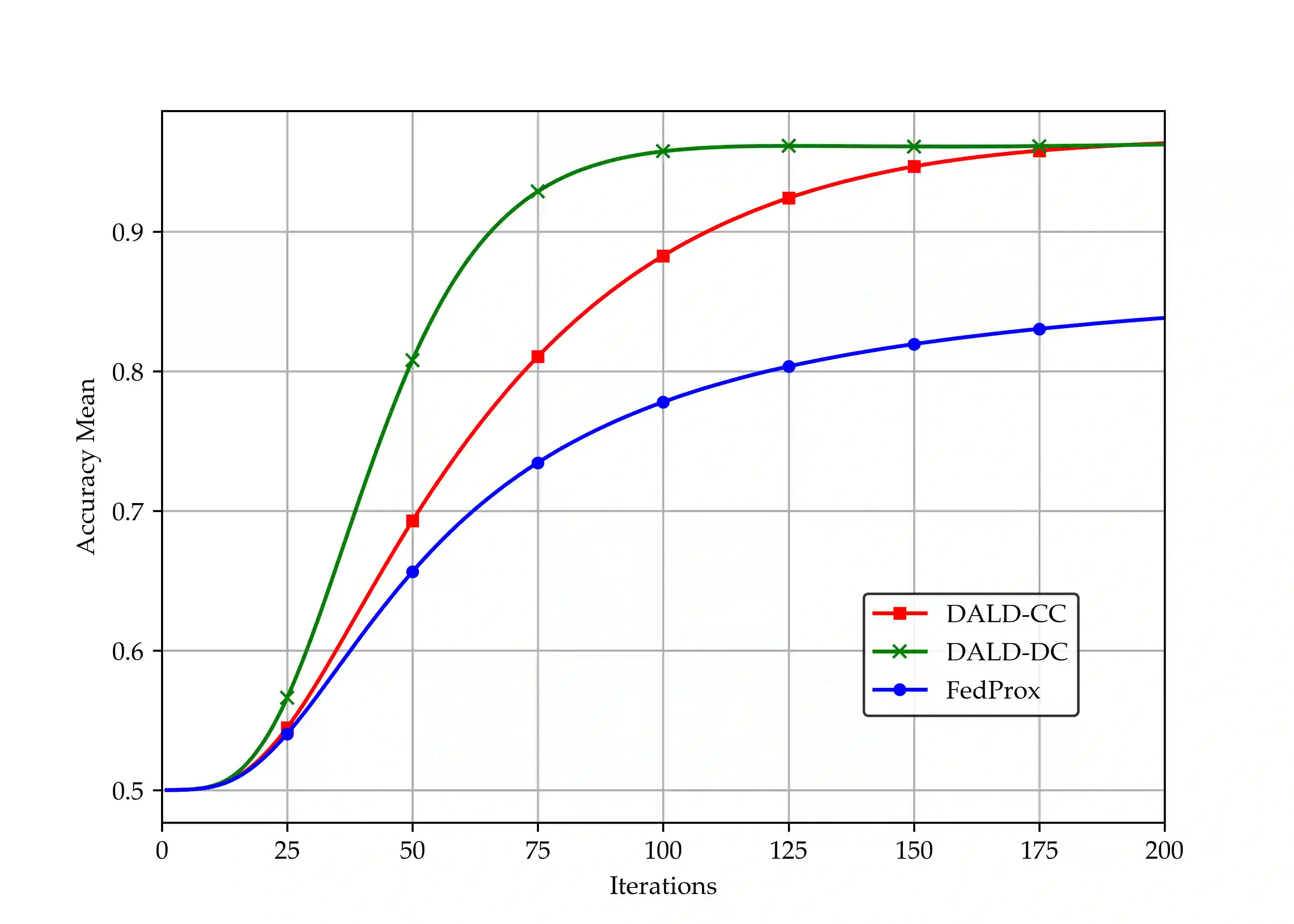
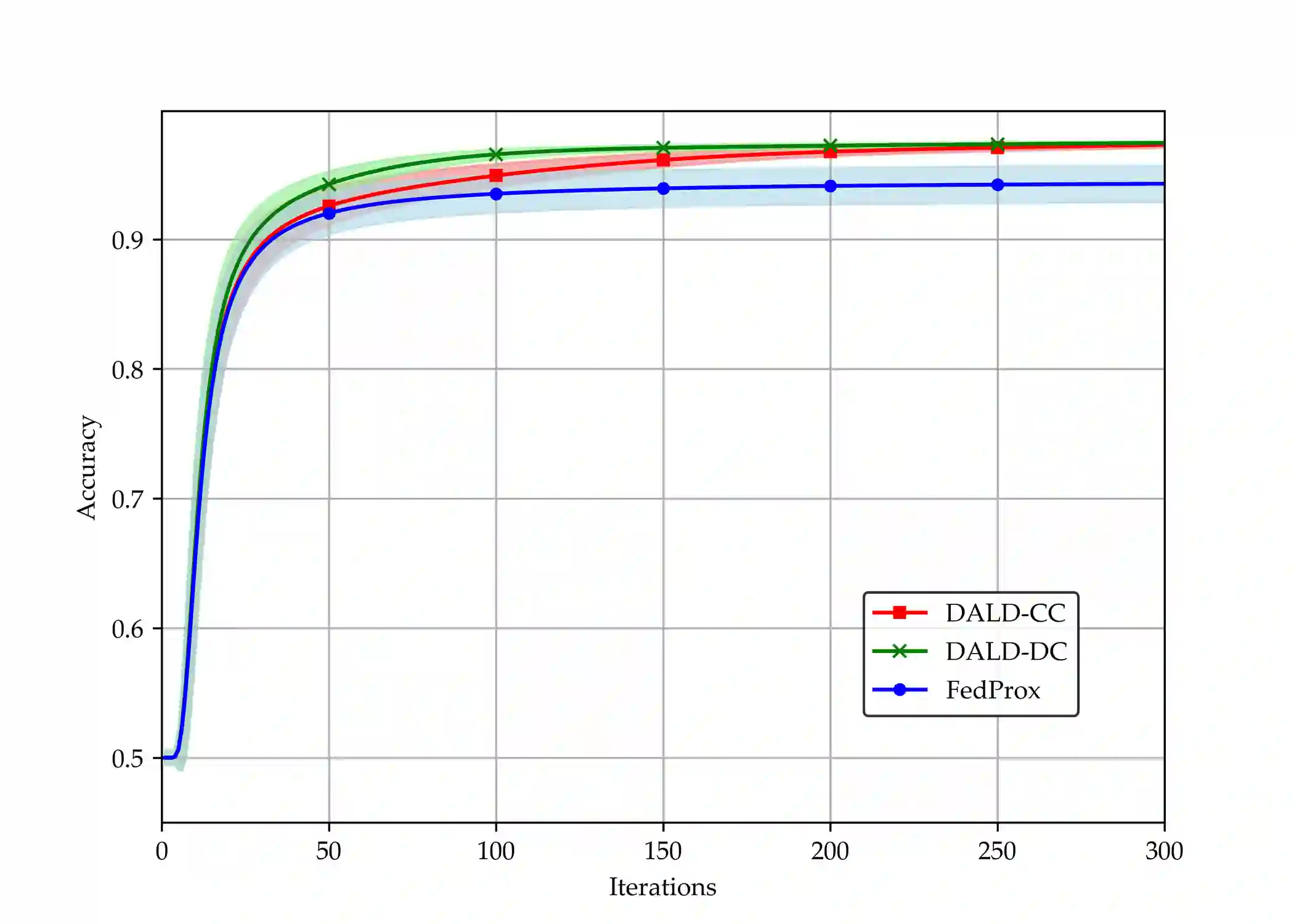
Federated learning (FL), as a distributed collaborative machine learning (ML) framework under privacy-preserving constraints, has garnered increasing research attention in cross-organizational data collaboration scenarios. This paper proposes a class of distributed optimization algorithms based on the augmented Lagrangian technique, designed to accommodate diverse communication topologies in both centralized and decentralized FL settings. Furthermore, we develop multiple termination criteria and parameter update mechanisms to enhance computational efficiency, accompanied by rigorous theoretical guarantees of convergence. By generalizing the augmented Lagrangian relaxation through the incorporation of proximal relaxation and quadratic approximation, our framework systematically recovers a broad of classical unconstrained optimization methods, including proximal algorithm, classic gradient descent, and stochastic gradient descent, among others. Notably, the convergence properties of these methods can be naturally derived within the proposed theoretical framework. Numerical experiments demonstrate that the proposed algorithm exhibits strong performance in large-scale settings with significant statistical heterogeneity across clients.
翻译:联邦学习(FL)作为一种在隐私保护约束下的分布式协同机器学习(ML)框架,在跨组织数据协作场景中日益受到研究关注。本文提出了一类基于增广拉格朗日技术的分布式优化算法,旨在适应集中式与去中心化联邦学习设置中的多样化通信拓扑。此外,我们开发了多种终止准则与参数更新机制以提升计算效率,并辅以严格的收敛理论保证。通过结合邻近松弛与二次近似对增广拉格朗日松弛进行推广,本框架系统性地涵盖了一系列经典无约束优化方法,包括邻近算法、经典梯度下降法及随机梯度下降法等。值得注意的是,这些方法的收敛性质可在所提出的理论框架内自然推导得出。数值实验表明,所提算法在客户端间存在显著统计异质性的大规模场景中表现出优越性能。