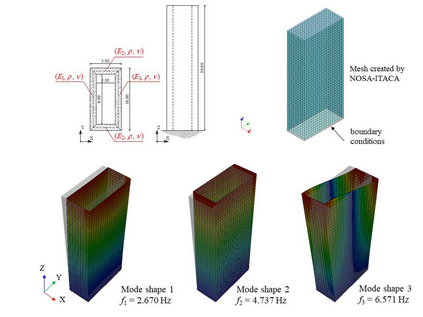
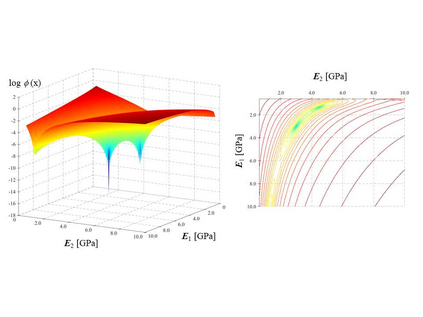
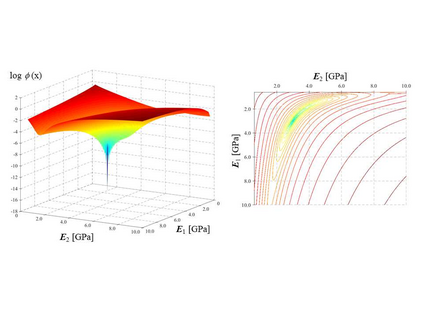
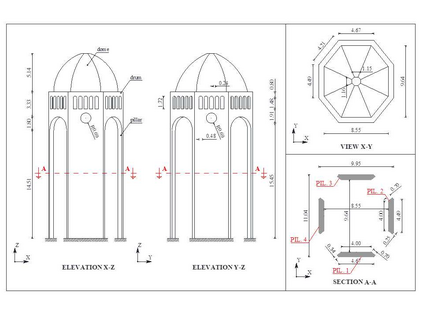
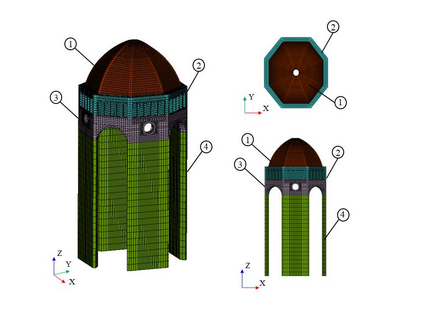
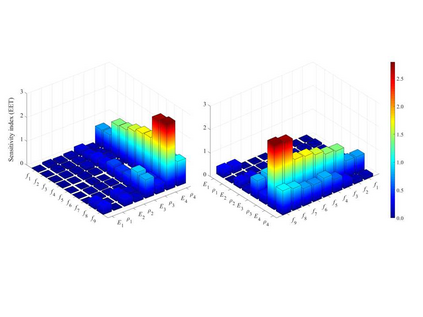
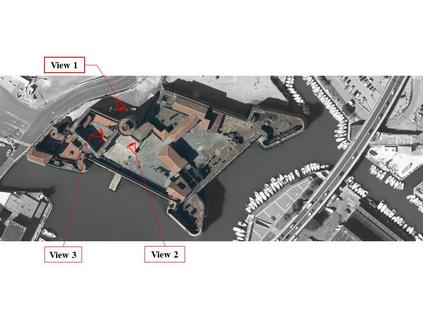
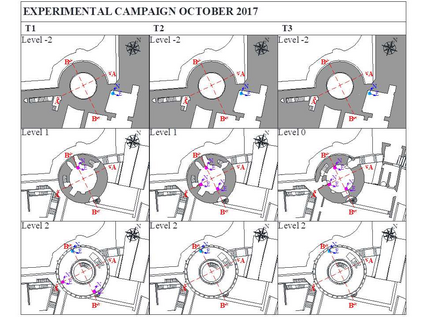
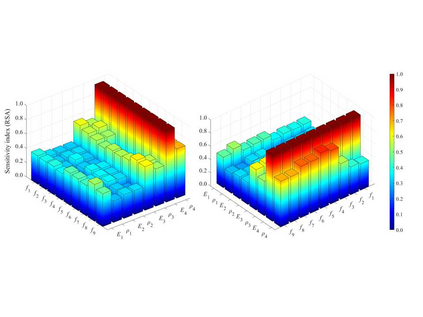
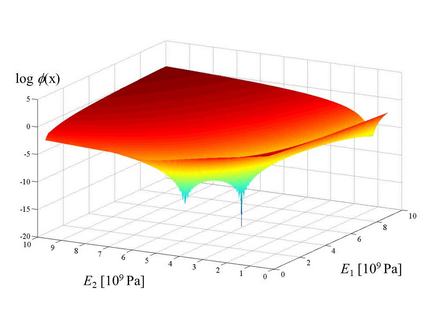
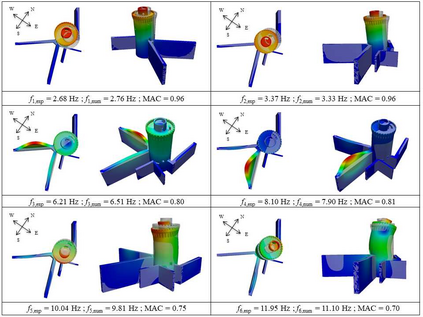
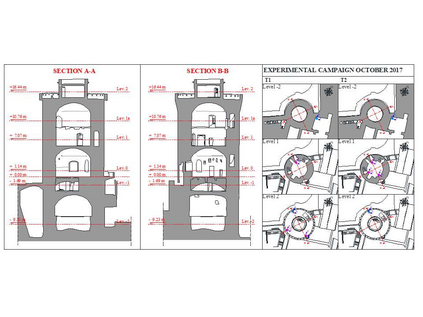
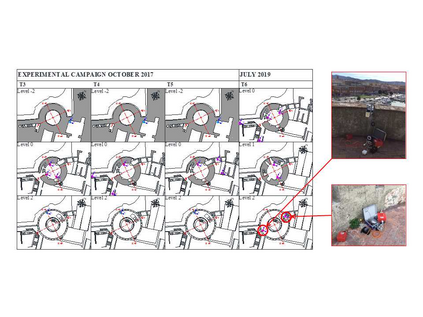
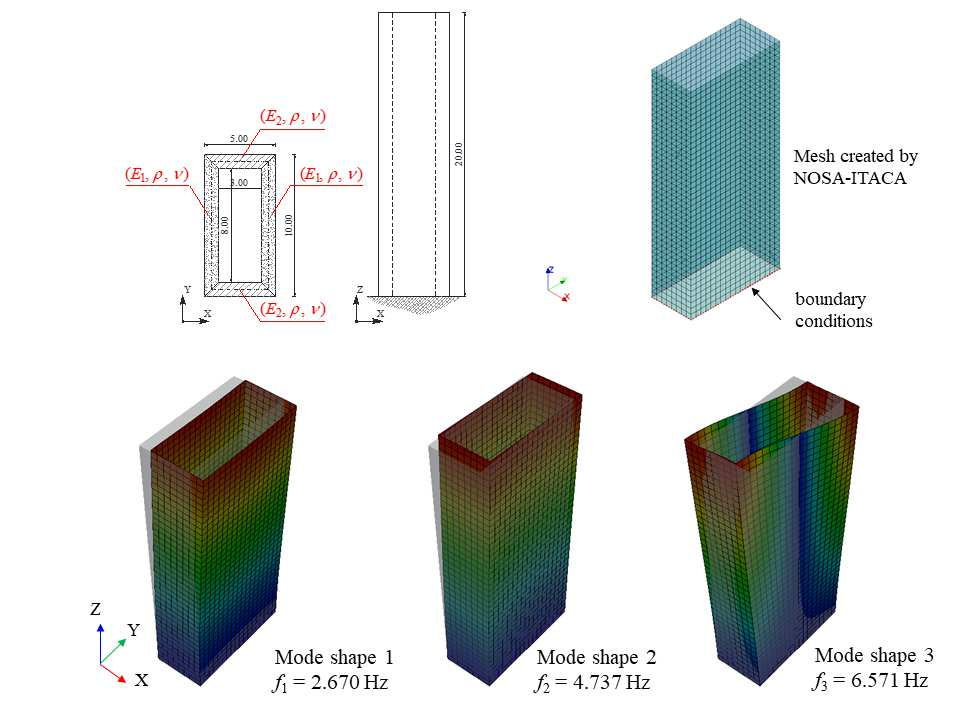
Finite element model updating of a structure made of linear elastic materials is based on the solution of a minimization problem. The goal is to find some unknown parameters of the finite element model (elastic moduli, mass densities, constraints and boundary conditions) that minimize an objective function which evaluates the discrepancy between experimental and numerical dynamic properties. The objective function depends nonlinearly on the parameters and may have multiple local minimum points. This paper presents a numerical method able to find a global minimum point and assess its reliability. The numerical method has been tested on two simulated examples - a masonry tower and a domed temple - and validated via a generic genetic algorithm and a global sensitivity analysis tool. A real case study monitored under operational conditions has also been addressed, and the structure's experimental modal properties have been used in the model updating procedure to estimate the mechanical properties of its constituent materials.
翻译:线性弹性材料结构的精度元素元件更新模型以最小化问题的解决方案为基础,目的是找到一些未知的有限元素元件模型参数(弹性模量、质量密度、限制和边界条件),以最大限度地减少一种客观功能,即评估实验和数字动态特性之间的差异。客观功能非线性地依赖参数,并可能具有多个本地最低点。本文件提出了一个数字方法,能够找到一个全球最低点并评估其可靠性。数字方法在两个模拟例子中进行了测试,即一个泥瓦塔和一个多米寺,并通过一个通用遗传算法和全球敏感度分析工具加以验证。在操作条件下监测的一项实际案例研究也得到了处理,模型更新程序使用了结构的实验模式特性来估计其组成材料的机械特性。