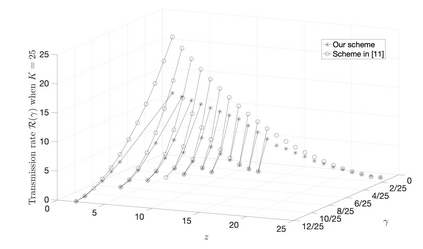
In this work, we consider a slight variant of well known coded caching problem, referred as multi-access coded caching problem, where each user has access to $z$ neighboring caches in a cyclic wrap-around way. We present a placement and delivery scheme for this problem, under the restriction of uncoded placement. Our work is a generalization of one of the cases considered in "Multi-access coded caching : gains beyond cache-redundancy" by B. Serbetci, E. Parrinello and P. Elia. To be precise, when our scheme is specialized to $z=\frac{K-1}{K \gamma }$, for any $K \gamma$, where $K$ is the number of users and $\gamma $ is the normalized cache size, we show that our result coincides with their result. We show that for the cases considered in this work, our scheme outperforms the scheme proposed in "Rate-memory trade-off for multi-access coded caching with uncoded placement" by K. S. Reddy and N. Karamchandani, except for some special cases considered in that paper. We also show that for $z= K-1$, our scheme achieves the optimal transmission rate.
翻译:在这项工作中,我们考虑的是众所周知的编码缓存问题的一个微小变体,称为多存码缓存问题,即每个用户都可以以循环包装方式获取近邻缓存的美元。我们提出这一问题的安置和交付计划,不受编码放置的限制。我们的工作是对B.Serbetci、E.Parrinello和P.Elia的“多存码缓存:超过缓存冗余的收益”中考虑的一个案例的概括化。确切地说,当我们的计划是专门为任何K\zäfrac{K-1 ⁇ K\gamma美元($)而专门为任何K$\gamma$($是用户人数,$\gamma美元是标准缓存规模。我们的工作是将我们的结果与这些案例的结果一致。我们的方案比“多存码缓存的多存的编码缓存的Rate-mory交易”中提议的计划要优于K.Reddy和N.