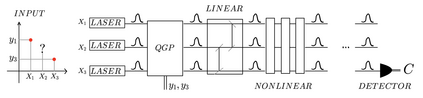
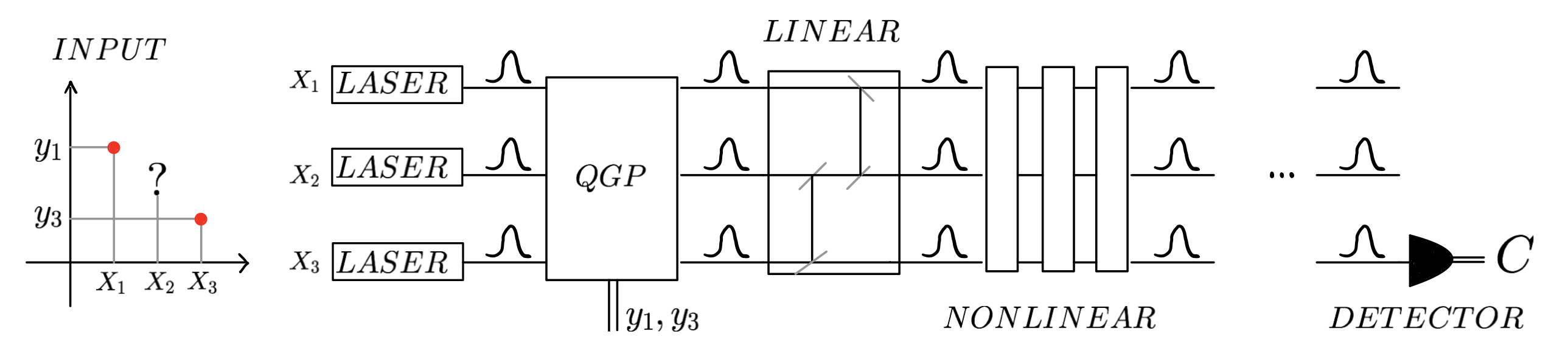
In this work we develop a quantum field theory formalism for deep learning, where input signals are encoded in Gaussian states, a generalization of Gaussian processes which encode the agent's uncertainty about the input signal. We show how to represent linear and non-linear layers as unitary quantum gates, and interpret the fundamental excitations of the quantum model as particles, dubbed ``Hintons''. On top of opening a new perspective and techniques for studying neural networks, the quantum formulation is well suited for optical quantum computing, and provides quantum deformations of neural networks that can be run efficiently on those devices. Finally, we discuss a semi-classical limit of the quantum deformed models which is amenable to classical simulation.
翻译:在这项工作中,我们开发了一种用于深层次学习的量子领域理论形式主义,输入信号在高森州编码,这是对高森过程的概括化,该过程将代理人对输入信号的不确定性编码。我们展示了如何将线性和非线性层作为单一量子门来代表线性和非线性层,并将量子模型的基本引力解释为粒子,称为“Hintons' ” 。除了为研究神经网络开辟新的视角和技术外,量子配方非常适合光学量子计算,并且提供了可以在这些设备上有效运行的神经网络的量变形。最后,我们讨论了可进行经典模拟的量变形模型的半经典极限。