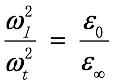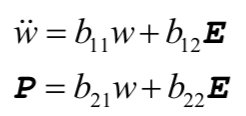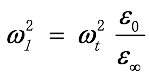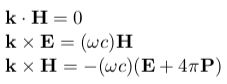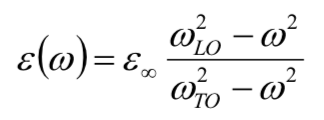从黄昆方程到极化激元——黄昆方程的历史意义和现实意义

从黄昆方程到极化激元——黄昆方程的历史意义和现实意义 | 纪念黄昆诞辰100周年

2019 年 6 月 8 日 中科院物理所

来源：公众号“返朴”（微信号：fanpu2019）

作者：王炳燊（中科院半导体所）、葛惟昆（北京大学）

2019年是黄昆先生诞辰100周年。朱邦芬院士曾将黄昆的贡献概括为：一本书、一组方程、一个理论、一种散射、一个模型。而先生自己最为满意的一项工作是黄昆方程。黄昆方程描述了离子晶体中晶格振动的声子与电磁场的相互作用，这改变了人们关于电磁模在晶体介质中传播的思维方式，并开创了后来的极化激元理论。谨以此文致敬黄昆先生。

在黄昆先生诞辰100周年之际，作为黄先生子弟和亲近后辈，我们缅怀先师的辉煌业绩，重温他对凝聚态物理学的卓越贡献。

黄昆（1919.9.2-2005.7.6），物理学家，中国固体和半导体物理学奠基人之一。

黄昆先生生前多次说过，他自己最满意的工作有两件，第一件就是1950年对离子晶体中的长波光学声子和宏观电磁场的相互作用的研究，即黄昆方程（有时也称Born-Huang方程，即玻恩-黄方程^[1]），另一件则是与晶格弛豫有关的多声子光跃迁 [Huang-Rhys参数，是黄昆与妻子A. Rhys（中文名李爱扶）合作的成果] 和无辐射跃迁理论。

黄昆先生对物理学的杰出贡献，按朱邦芬院士的归纳^[2]，可以概括为

一本书：玻恩、黄昆的《晶格动力学理论》^[3]，这本书被国际物理学界奉为经典；

一组方程：即本文重点介绍的黄昆方程^[1]；

一个理论：黄-里斯（Huang-Rhys）关于多声子跃迁的理论^[4]，以及他后来统一的关于多声子无辐射跃迁的理论^[5]；

一种散射：关于晶体中杂质引起的X射线散射——黄散射^[6]；

一个模型：关于半导体超晶格的黄-朱模型^[7]。

黄昆先生的工作博大精深，本文仅集中讨论黄昆方程出现的历史背景以及这一组方程的方法和结论对固体物理学（即现在统称的凝聚态物理学）在当时和对后来发展的重大意义。

黄昆方程

上世纪40年代，固体的电子态理论才起步不久，对于实际材料的各种性质的理论计算才刚刚开始。因此对于固体的物理性质的理论研究，都是从理论上认识比较清楚的离子晶体开始。黄昆先生那一代物理学家，都注意到介电函数是关键的物理量，因为它不仅决定物质的电学性质，而且决定物质的光学性质。对许多纯净的离子晶体而言，在可见光波段它们是透明的，而在红外波段则有许多丰富的现象。而这又与固体的一类晶格振动即光学声子（即晶格内不同原子、在离子晶体中是正负离子的相对振动）谱紧密联系。

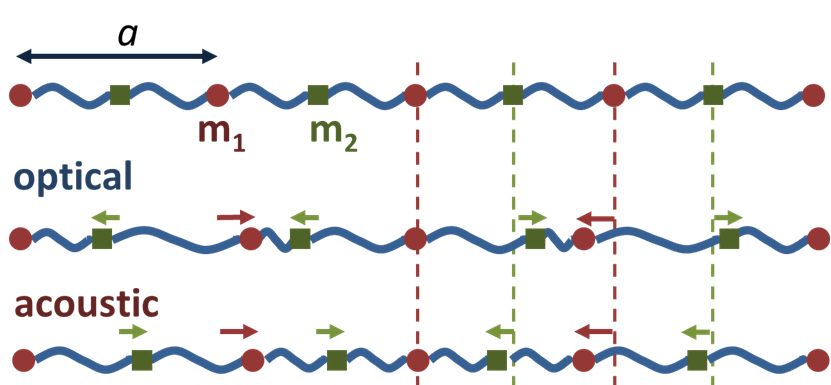
固体由若干原子（原子实与电子）按一定方式组合而成，这些粒子相互作用，形成一个巨大的多粒子系统。固体晶格振动的简正模能量量子被称为声子。离子晶体中正负离子相对振动形成长光学波，质心的振动形成长声学波。| 图片来源：维基百科

黄昆方程正是把光波与光学声子关联起来。一开始人们没有意识到它的重要价值。一个真实的故事是，当黄昆方程的论文投稿时，审稿人认为该文只是重新证明了著名的Lynddan-Sache-Teller关系^[8]，即纵光学波频率 ω_l和横光学波频率 ω_t之间的关系：

其中 ε_∞ 和 ε₀分别为高频（频率远高于声子频率）和静态（ω=0）的介电常数。审稿人坚称黄昆的论文只是LST关系的另一种证明而拒稿。幸亏黄昆先生的老师莫特教授（N.F.Mott，1977年获得诺贝尔奖）了解这篇文章的重要意义，亲自出面推荐才得以发表。

LST关系把声子的两种本征频率和作为宏观可测量的介电常数联系起来，而不需要离子晶体内部相互作用的细节，因此是一个普遍的关系，具有重要的意义。

那么黄昆先生的工作与LST关系的工作有什么不同呢？

从具体的物理图像对应的基本原理出发，而不是跟随别人已有的工作，是黄昆科研实践的一个显著特点，也是他能够成功原始创新的重要因素。黄昆天才地把电场E和磁场H所满足的麦克斯韦方程和光学声子的振幅w的动力学方程联合起来，他所提出的光学声子振幅的动力学方程为

这就是著名的黄昆方程，它把光学声子的振动动力学与晶体的极化和外加电场（即光波中的电矢量）巧妙而合理地联系起来。这组方程在本质上与许多重要的物理方程一样，不是推导的结果，而是基于高度的洞察力，对物理原理的抽象概括。牛顿方程和薛定谔方程也不例外。这个方程与麦克斯韦方程相联合，经过细致的推导，最后得出，对于纵波，有k//E//w，同时k·D=k·(E + 4πP)=0，进而得出：

这个结果和LST 关系式完全一致，但出发点完全不同。

黄昆的新贡献更在于，他进一步引入了电磁波传播的迟缓（Retardation）效应，即离子之间库仑相互作用不是瞬时发生的。此时必须考虑麦克斯韦方程组中的其它几个方程：

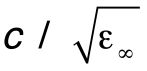
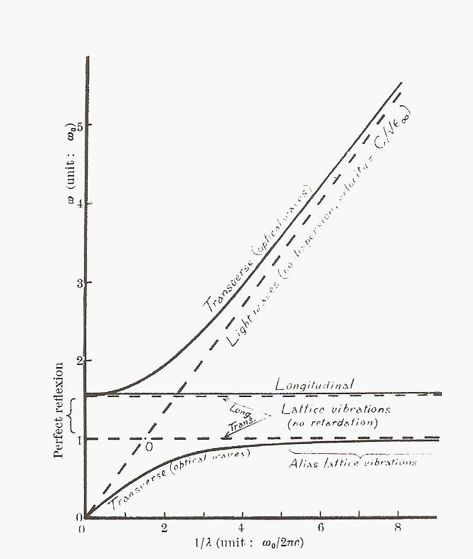
所得到的解表明，光波只受到电子（速度为）以及LO和TO声子折射的作用。其结果是纵向光学声子LO不受影响，而横向光学声子TO在其色散曲线与光子色散曲线相交之处（参看附图）形成共振、产生强烈的相互作用，由此得到一种新的色散关系：

这是前人从未得到过的结果，如图1所示。横向光学声子TO的特殊性，恰好反映了光波的横波性质。

光波与晶格振动，参见 Born & Huang 原著。图中两条水平的虚直线表示（上）纵向光学声子LO和（下）横向光学声子TO的色散关系。在这两条线之间不存在极化激元，光波几乎完全被离子晶体反射，这也就是所谓的剩余射线带。斜的虚直线表示光子的色散关系。两条实曲线表示极化激元的色散关系。在横向光学声子TO与光子的色散曲线相交的点附近，光子与声子形成共振，发生强烈的耦合。

黄昆的结果，完美地表现了离子晶体的红外色散特性，还完美地解释了所谓的剩余射线带（reststrahlen，即晶体中光的禁带，表现为全反射）带的物理起因。他指出，如果把上图旋转90度，就直观地解释了色散现象。两条竖直的虚线之间就是剩余射线带。

从黄昆方程到极化激元

黄昆方程最重要的意义，可以用美国著名物理学家E. Burnstein ^[9]在第17届国际拉曼会议上对黄昆的评价来概括：“Huang has changed our way of thinking about propagating EM mode in crystalline mediums”（黄昆改变了我们关于电磁模在晶体介质中传播的思维方式）。其实这里的介质，不止是离子晶体，而是包含了一切有光在其中传播的介质。由于黄昆方程直接利用了电场与偶极子的相互作用，它也同样适用于一切具有偶极矩的元激发与光波的相互作用，具有普遍意义。这也正是后来光波与激子（exciton）耦合的极化激元（polariton）的原始物理基础。

在人们传统的理解中，光进入固体以后，就以真空光速除以介电常数的速度传播，再通过电场的极化作用，激发光学声子或其它元激发。而现在黄昆指出，不是这样的，光进入固体后，就与贡献介电常数的元激发（不只限于横偏振光学声子）相互作用，而耦合在一起传播。并且对同一个波矢，会存在两个频率的波，其中每一个波的电磁波和机械振动成分和相应的能量所占的比例随频率变化。特别是，横、纵元激发的频率不同，在这两个频率之间，电磁波不能传播（如果不考虑元激发的色散）。这是一个全新的物理图景，彻底颠覆了光波独立传播、不与元激发耦合的传统观念。这一思维方式的转变，在各种物理现象中具有普遍的和重要的意义。黄昆方程也使人们对介电常数的意义有了更深入的理解，达到一个新的高度；而且这样表示的介电常数，也与后来由严格的线性响应理论导出的完全一致。

必须指出，虽然黄昆方程组是以经典电动力学和经典力学来表述的，但是其实质内容和结论与量子力学和量子方法的表述完全一致。J. Hopfield ^[10]在1958年的著名的关于光子与激子耦合的工作就证明了这一点。激子与光子耦合的色散曲线与附图所表示的完全一致，只是纵横声子变成纵横激子。实际上，把黄昆方程开创的这种电磁波（光子）与晶格振动（声子）的耦合予以量子化，就成为一种新的准粒子。 Hopfiled ^[10]在1957年命名为，polariton中文一般译为为极化激元（有人提议翻译成电磁耦合子，黄先生自己在私下则表示应当称为色散子，因为它完整地描述了固体的色散），现在甚至出现了polaritonics的名词，俨然已经成为一门新的子学科，可见其学术和应用上的巨大影响。由于黄昆在论述过程中已经成功地把宏观电场和微观电场分离，因此，虽然固体中电子和声子态的理论研究已经有了非常大的改变和发展，但黄昆方程仍然保持着它旺盛的生命力。

多种多样的极化激元

物理学本质上是一门实验科学，这样一种物理上全新的图景，不仅引起理论工作者的注意，也理所当然地吸引了实验工作者希望用实验证实极化激元的存在。C. H. Henry 和J. J. Hopfield ^[12]在磷化镓（GaP）中用拉曼散射证明了极化激元的存在，准确测量了其中极化激元上下两支的色散曲线，证明了极化激元理论的正确性。由于半导体中激子有的也有偶极距，因此也能形成极化激元，虽然激子具有明显的色散，而原始的黄昆方程中没有包括光学声子的色散（一般色散比较小，这也是晶格振动爱因斯坦模型的由来），但是方程完全可以不加改变地扩展到包括色散的情形。J. L. Birman等人 ^{[13, 14]} 发展了激子-极化激元（exciton-polariton）的布里渊散射理论，而在1977年，C. Weisbush等^[15]在砷化镓（GaAs）中进行布里渊散射实验，结果完全与理论符合，进一步证明了极化激元理论的正确性。

说到激子的色散，极化激元理论还给出了一个新的物理现象，即某一频率的光进入固体后，在一定条件下会变为两支快慢不同的波，被称为附加波（additional wave）^[16]，并引出了所谓附加边界条件（additional boundary condition）问题，在一段时间内成为研究热点。而光学声子的色散所引起的半导体超晶格中与电磁波相互耦合所产生的复杂现象，直到上世纪80年代末才由黄昆先生本人和朱邦芬^[7]提出的黄-朱模型予以阐明。

实际上，固体中能与电磁波耦合的运动模式不限于声子和激子，相互作用也不限于光与电偶极子。在电偶极子被禁戒的情况下，与磁偶极子等都可以形成极化激元，因此在现代物理中，有各种各样的极化激元，如自旋波极化激元等。极化激元这一概念已经深入到物理学的许多领域。比如等离激元（plasmon）、表面等离激元与电磁波的耦合、光子晶体等领域，都是这一理论的扩展。1972年，在意大利的Taormira召开了第一届极化激元国际学术会议，由于时值文化大革命，黄昆没能参加会议，但他在1951年的开创性工作得到与会者的高度评价，而他那篇二十多年前的文章被列入会议文集^[17]，这几乎是史无前例的。黄昆先生是当之无愧的极化激元理论的开创者。

1905年，玻恩把长声学声子的微观参量和宏观参量即弹性系数和泊松比联系起来，三十五年后黄昆方程把长光学声子的微观参量和宏观的介电常数和色散性质联系起来。这是一个伟大的传承和发展。同时，黄昆方程把纵光学长波振动与宏观电场相联系，为后来H.Frohlich^[18]提出著名的电声子极性相互作用理论奠定了基础。从更广泛的视野来看，黄昆先生这件工作的重大意义还不止于此。一般来说，相互耦合的两个系统是同质的，而极化激元是由声子和光子两种不同的玻色子耦合而成的，这是量子力学态叠加原理的体现，具有启发性的意义。

时至今日，如果以“polariton”作为搜索词来检索，那么将会得出成千上万的结果。可以毫不夸张地说，任何与物质的光学性质相关的研究和技术应用，都与以黄昆命名的方程或远或近地相关联。黄昆方程和同样由黄昆先生开创的与晶格驰豫相联系的多声子光跃迁理论和无辐射跃迁理论，以及黄散射等一系列原始创新的理论成果，都是凝聚态理论发展道路上光辉的丰碑，是值得我们永远纪念和学习的！

先生的音容笑貌依然历历在目，先生的谆谆教诲永远牢记心中。谨以此文，献给敬爱的黄昆老师和李爱扶（A. Rhys）师母！

作者对朱邦芬院士的宝贵意见深表谢意。

参考文献

[1] K.Huang, Proc. Cambridge. Phil. Soc. 45(1049); pp452-462, K.Huang, Nature, 167, 79(1951); K.Huang, Proc. Roy.Soc. A208, 352(1951)

[2] 《黄昆》，朱邦芬，贵州人民出版社，2004.

[3] 《Dynamic theory of crystal lattice》, M. Born and K. Huang, Oxford University Press, 1954; 《晶格动力学理论》（中文版），马克斯玻恩，黄昆著，葛惟昆，贾惟义译，北京大学出版社，1989.

[4] K. Huang, A. Rhys, 1847, London: Proc. Roy. Soc. 950, A (204), 406-424.

[5] 黄昆，中国科学，1980（23），949-954.

[6] K. Huang, London: Proc. Roy. Soc.,1947, A (190), 102-117.

[7] K.Huang, B.F.Zhu, Phys.Rev.B.38,13377(1988)

[8] R. H. Lyddane and K. F. Herzfeld, Phys. Rev. 54, 846 (1938); R. H. Lyddane, K. F. Herdeld and R, G. Sachs, Phys. Rev. 56, 1008 (1940).

[9] Burstein E, Proceeding of the 17th coference on Raman spectroscopy, International steering Committe ICORS 2000, New York, John Wile& Sons Ltd.(2000) p.40

[10] J Hopfield ,Phys. Rev. 112, 1555（1958）

[11] С.И.Пекар, ЖЭТФ Т.33, 1022 (1957) [Sov. Phys. JETP, 6, 785 (1958)]

[12] C.H.Henry and J.J. Hopfield, Phys.Rev.Lett. 15, 964-966(1965)

[13] B.Bendow,J.LBirman, Phys.Rev.B4,1678-1686(1971)

[14] W.Brenig, R Zeyler,J.L.Birman, Phys.Rev.B5,4617(1972)

[15] R.G.Ulbrich, C.Weisbush, Phys.Rev.Lett.; 33,865(1977)

[16] S.I.Pekar, Journal of Luminescence; Vol.20,No.4,333(1979)

[17] Burstein E, Martini F, Polariton, New York, Pergamaon Press (1972) Phys.Rev.Lett. 33, 865868 (1977)

[18] H.Frohlich, Proc. R. Soc. Lond. A 215, 291(1952)

来源：返朴