打破惯用范式，以数学与统计构建新一代人工智能方法论

2019 年 5 月 13 日 PaperWeekly

当前人工智能面临如下重大的理论挑战：可计算性、可解释性、泛化性，以及稳定性。围绕这些基础问题，北京智源人工智能研究院从数学、统计和计算的角度，设立了 “人工智能的数理基础”重大研究方向，并在该方向首先启动了三方面研究（可解释性的新型人工智能模型，新型的机器学习算法，深度学习的基础理论），以期打破基于计算机实验和神经科学的人工智能的惯用建模范式，建立以数学与统计理论为第一原理的新一代人工智能方法论。

2019 年 5 月 9 日，由北京智源人工智能研究院（Beijing Academy of Artificial Intelligence，BAAI）主办的“智源论坛——人工智能的数理基础”系列报告第一场开锣（参与5 ⽉ 13 ⽇及 16 ⽇的后续论坛，请关注文末信息）。

北京⼤学教授夏壁灿

上午 9:00，本次论坛在北京⼤学教授、智源研究项⽬经理夏壁灿的主持下正式开始。活动伊始，智源研究院副院长刘江代表主办方致辞，在介绍中他重点强调了支持科学家勇闯人工智能科技前沿“无人区”的智源学者计划，以及智源与北京优势高校院所和骨干企业共建联合实验室，开展跨学科、大协同创新攻关所开展的工作。

北京智源人工智能研究院副院长刘江

论坛当日，包括北京⼤学副教授董彬、北京⼤学研究员林伟、北京⼤学副教授邵嗣烘、北京应⽤物理与计算数学研究所副研究员王涵，以及北京⼤学教授张志华在内的五位学者分享了他们在人工智能数理基础领域的研究探索——当数学撞上人工智能，当纯粹的数学思维来求解智能，又会得到怎样的意外之喜？下面就带你一站式回顾此次论坛的“重点笔记”。

董彬：走出牛顿的苹果园，从大量数据中推出科学规律

北京大学副教授董彬

作为青年千人计划⼊选者、国内图像处理领域⻘年学术带头人，北京大学的董彬副教授还建立了图像科学两大数学方法的联系，并在数学领域顶级杂志 JAMS 上发表论文。他此番率先带来了《Bridging Deep Neural Networks and Differential Equations for Image Analysis and Beyond》主题报告，探讨数值微分方程启发深度学习建模，即如何在深度神经网络和微分方程之间建立联系，重点围绕其团队近两年的研究成果展开分享。从应用或计算数学的角度来来理解深度学习，希望架起这个桥梁之后可以给网络构架的设计，以及一些理论相关的研究提供一些新的指导思想。

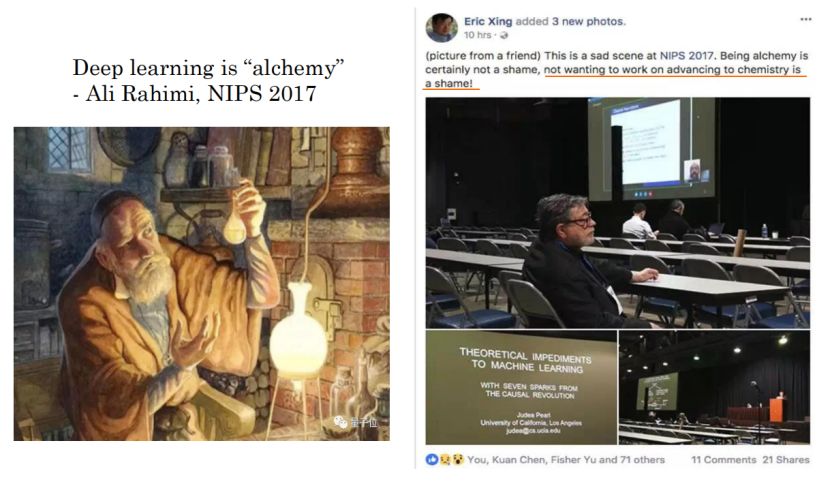
据 Google Trends 数据显示，自 2015 年起，深度学习的关键词搜索频率开始呈快速上升趋势。除却 AlphaGo 等里程碑式的优秀成果之外，深度学习也不可避免地存在着诸多问题，Ali Rahimi 在2017年的NIPS颁奖礼上就曾做过一个报告，提到“Deep learning is ‘alchemy’” ，这里的“alchemy”就是所谓的炼金术，很多人都认为深度学习就像炼丹一样，把你的 formula 塞进去过个几个小时或者一两天才能看到结果，但却不知道下一步应该怎么调，只能通过尝试。

谈及此，董彬还重点介绍了邢波（Eric Xing）针对这句话提出的一个观点，即“Being alchemy is certainly not a shame，not wanting to work on advancing to chemistry is a shame! ”——化学的前身就是炼金术，在没有系统理论指导的情况下是炼金术阶段，但被赋予系统的理论指导之后就从一个看似纯实验的学科变成有一定理论体系的科学，这也是所有想做基础理论学者的目标——赋予深度学习一套科学理论，做到 Mathematical / Theoretical Deep Learning。

之所以要这么做，是因为如今看起来长势甚好的深度学习仍然面临着各种各样的挑战：

标注缺乏（或者说非常高质量的标注相对缺乏）：即便已被广泛使用的ImageNet，label 的噪声也很大。即使标注非常丰富的计算机视觉领域也会有碰上各种各样的问题，更何况是在标注难以获得的生物医疗领域。
如何在多样的数据上学习：AI 的应用落地需要足够广泛的适用场景，因此模型也需要从不同的数据类型中学习，因为人类作出判断不仅是看一张图像，而是结合诸多信息，通过各种各样异构的数据作出决策。怎么样在多样的数据上学习，依然是挑战。
使深度学习模型更加透明：深度学习的效果时好时坏，正误尤为极端，时而完美，时而又错得离谱，其间问题为何？我们希望能够借助在设计时（设计网络构架/设计模型/设计优化算法）提供理论指导，从而使深度学习更加透明。而这最后一点挑战也恰恰是人工智能数理基础关注重点。当下的深度神经网络不透明，调参数、训练，再到测试人人可为，却无人能解其深意，这正是该项研究要解决的问题。

如何提供指导？许多优秀的数学家正在通过很严谨的理论分析去证明部分性质，但董彬团队走了另外一条路——先探寻深度学习训练及网络构架与数学中的哪些概念有关系，找到这个关系后就知道从哪里开始分析。例如可将深层网络理解成微分方程，或者将网络构架理解为微分方程的的一种离散形式，在这种情况下，网络训练对应的就是 Optimal Control，包括强化学习也可以用连续控制的观点来看待。据可考资料显示，最早提出这个观点的是鄂维南，他在 2017 年的一篇文章里分析了残差网络（Residual Networks, ResNets）和动力系统的关系。

这个桥梁一旦搭起，基本上就可知道从数学中的哪个领域出发去理解深度学习。鉴于此二者近年来相对独立的发展态势，彼此有很多思考可供借鉴，拓宽思路之余也会发现很多有趣的新应用。

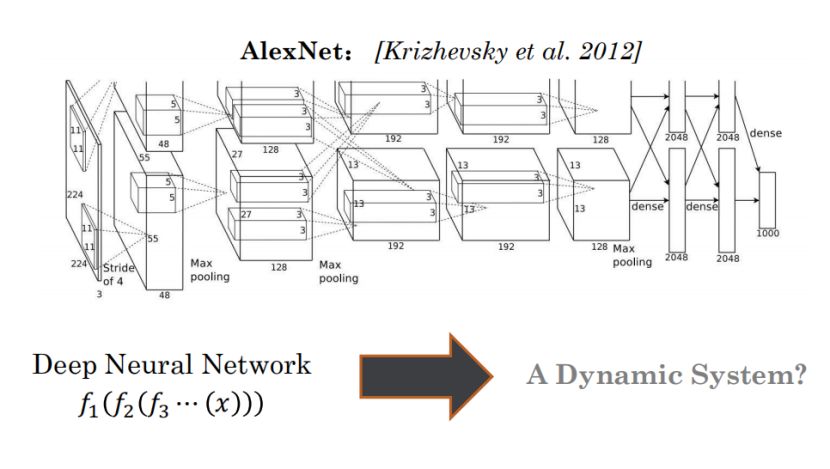
我们先来看 DNN（深度神经网络，主要是卷积网络）和数值 ODE 之间的关系。以 AlexNet 为例，若要用数学形式写出，可以将其看作一个动力系统，但是这样的动力系统很难分析，因为缺少特殊结构，这样一般形式的动力系统不知该如何入手。

相比之下，如果把残差网络的数学形式写出来，就很容易看出它是对下面这连续的 ODE 基于时间做了前向欧拉离散，只不过在网络设计时把 Δt 设成了 1。有些工作已经发现，把 Δt 设得更小，训练反而更加稳定。

这是很有意思的观察，但还要考虑残差网络和动力系统的联系是否是特例或偶然，还是一般规律。更重要的是，假如我们建立了 Numerical ODE 和网络构架这样的联系，那么能否从 Numerical ODE 这一发展了几十年的领域中去反推出一些有用的构架？而反推出的构架很多时候都是新的构架，那这些新的构架到底有没有用？这是董彬想回答的两个问题。

除此之外，深度学习训练时还会遇到各种随机扰动，这可提升训练效果。如果在训练时加上一些随机扰动，比如随机加一些噪声，那么其对应的动力系统是什么，自然而然地会想到随机偏微分方程。到底是不是呢？有两个例子，一个是 shake-shake，一个是 stochastic depth，都是对于残差网络设计的随机扰动训练。

也就是说不管用随机策略，还是网络自带的随机性质，训练它时，实际上都是在求解一个随机控制的问题，所以可以从随机控制的角度来看待这个带有随机训练策略的深度学习训练。

总而言之，董彬的目标是建立起数值 ODE 和网络构架设计之间的关系，并借此从计算数学反推网络构架。利用数学的直观，设计网络构架时就知道应该对深度是有压缩，知道其可能带来的性能提升，也可以解释为什么有这样的提升。

在我们拥有海量数据前，提出新的科学假设往往基于人类观察的现象（苹果坠落之于牛顿），如今，采集数据的手段越来越先进，大量三维甚至四维的数据涌入，我们怎么能够通过大量数据来提取规律？

数据科学的终极目标就是利用计算，然后从大量数据中发现新的规律。一方面 PDE 是描述很多动态数据非常自然的工具，另一方面深度学习又是表达能力及学习能力都非常强的工具，能否将两者结合？关于这一点，董彬想要应用的主要场景是生物和医学的动态分析，以及如何用深度学习结合 PDE，结合传统的建模思想，解决很多历史遗留问题。一者希望能够利用深度学习的强学习和强表达能力，再者希望借助 PDE 给深度学习模型一定的可解释性。

董彬介绍了他们团队如何利用深度学习端到端的训练思想和深层网络强大的表达能力，结合数值PDE方法，提出一个如何从海量数据中学习未知PDE模型并同时能做精确预测的算法框架“PDE-Net”。PDE-Net的特点如下：

自然地将先验信息与网络构架相结合，即将模型驱动与数据驱动相结合；
在训练PDE-Net时，给其中的卷积核做适当的约束使其能够逼近各阶微分算子，赋予神经网络一定的透明度（这一灵感来自之前的理论研究）。因此，PDE-Net能够在保证预测能力的同时也保证模型的可解释性。

分享最后，董彬对此次的报告内容做了一个简要总结，并对未来的研究方向做了一个大体汇报：我们之前的工作实际上是在 Numerical Differential Equation 和 Deep Nearchitecture 之间搭起一个桥梁，很多时候这个桥梁是经验性的，因为目前我们还缺少理论，只是做了一个直观性的观察。但现在通过观察提出一些新的网络构架，实际效果也不错，下一步希望能够借助智源的支持，做一些理论分析。还有就是通过搭起这个桥梁，我们是否能够从数学角度出发设计出更加 robust 或者说更加紧致的深层网络，因为现在的网络很容易被攻击，而且参数巨多无比，很难在边缘设备上实现。此外，我们希望能够真正尝试从真实的生物学动态数据里面去学一些 principles。

林伟：维数的灾难？维数的祝福！

北京大学研究员林伟

同样是青年千人计划⼊选者，北京大学研究员，国内统计学习领域的⻘年学术带头⼈林伟的报告主题为《破解机器学习中的维数灾难：从可辨识性谈起》，重点分析了高维统计比较关心的一个核心的问题。近年来，以深度学习为代表的“黑箱”机器学习算法在应用中获得了巨⼤成功，但缺乏可解释性和严格的理论基础。⽽可辨识性和维数灾难的概念是从统计学⻆度理解深度学习与机器学习算法的关键。

所谓维数灾难，就是说深度神经网络可以看成是一类过参数化的模型，数据相对于参数来说少得多，或者反过来说，参数相对于数据来说多得多。这通常会被认为是一个灾难，而林伟在报告开篇便站到了另外的一个角度，不谈维数的灾难，反过来强调了维数的“祝福”。

而所谓可辨识性，林伟也做出了阐释：f 是密度函数、分布函数，如果两个参数 θ₁、θ₂ 所对应的数据分布是一样的，那么能够推出一定是同一个参数，这就是可辨识性。也就是说从可以观测到的数据，能够辨识出参数应该是哪一个，或者可以说它的逆否命题也是对的，如果两个参数值不一样，那么它所导致的可观测数据的分布也不可能一样。

这很关键，如果不具有可辨识性，就没办法确定真实参数是什么，因为有两个不同的参数导致同样的分布。这种情况下，若是用一个算法去优化找这个参数，有时候可能跑到 θ₁，有时候比较接近 θ₂，就会非常不稳定，所以不可辨识模型也就面临着诸多缺点：

解释性差：如果你不确定 θ₁、θ₂ 到底哪一个是对的，自然无法解释 θ₁ 是什么意思；
预测（泛化）能力不稳定：正确性难以保证；
理论保证难：如果没有可辨识性，就根本不知道目标在哪儿，没有努力的方向，也不知道要保证什么。

这里的困难在于，如果一个模型是过参数化的，一般就不具有 identifiability。因为当参数个数远大于样本量时，最多进行到二层就无以为继了，因为没办法解，这个方程组有无穷多个解，特别是这个模型非常复杂，像 Deep Learning 这种有非常多的隐含层的时候，就更不知道中间的这些参数到底是不是唯一确定的了。

为了保证可辨识性，可以采取稀疏和低秩两种方法，事实上后者也属于稀疏性。这在高维统计已经做得非常成熟了，很多情况下我们提的条件中都隐含了可辨识性。但如果不能满足精确可辨识，是不是就无计可施了？我们去看一下文献，因果推断理论有很多情况实际上是不可辨识的，因为因果推断实际上极其难，无法给出点估计，但可以定界。因而便引出了近似可辨识性这样一种新的理论框架。

而可辨识性和维数灾难的概念正是从统计学角度理解深度学习与机器学习算法的关键。

邵嗣烘：人类的终极在哪儿，我们为什么知道我们是我们？

北京大学副教授邵嗣烘

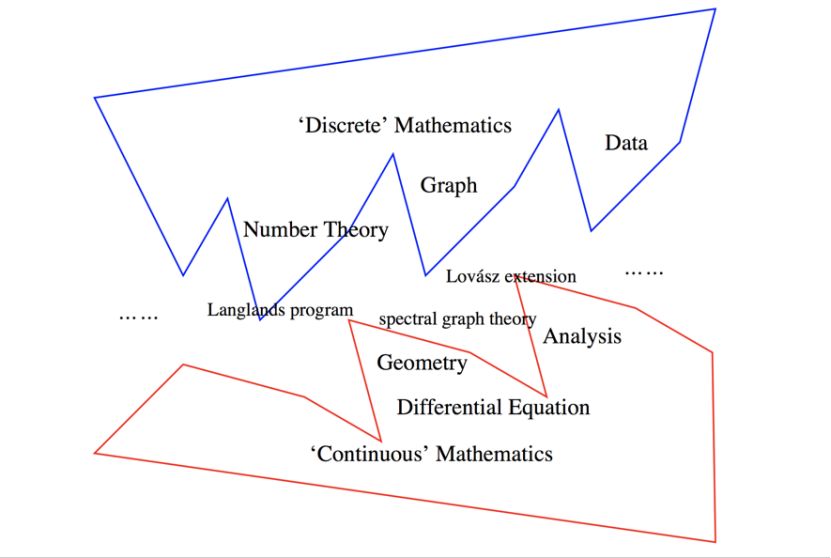
北京大学副教授邵嗣烘带来了《面向智能的数学》主题报告，探讨在脑神经⽹络上建⽴数学模型来剖析由物质世界的物理定律演变成思想世界的意识智能的过程。现在谈到网络，很多人会在计算机里做成一张图、一些点，画边连起来。但如果你用这个方法去研究人的大脑，生成的图会非常庞大。前者是一条连续的线；后者则是一个个离散的点，这二者虽然都叫数学，但离散数学更多是在计算机这边关注，连续数学就是大家常说的那一类。邵嗣烘的观点是，应该有一个更大的框架，把这两个东西放在一起考虑。他自己做的工作就是把一些离散的东西通过某一种变化变成连续的东西，因为连续的数学里面有很多很强大的工具，有这么多年的积累可以使用，只要转化过来，就可以尝试通过其中的工具解决问题。

邵嗣烘一开场便甩出了人类的终极问题——我们人类现在在哪儿，从何处来，又要到何处去？并紧接着发问，“在这些终极问题之前，我们是否应该问问自己，‘我们为什么知道我们是我们’？”这就涉及到我们人脑是怎么形成意识，或者说人工智能何解。所谓人工智能，其根本上就是想通过我们目前理论能够理解的方式去模仿智能或者探索智能的机理，但是离不开“人工”两个字就是它就一直是人工的，我们想做的事情是在这个这终极问题上做一个可能的探索。

人的意识会带来非常美妙的东西，牛顿被苹果砸到脑袋，想出了万有引力定律；张益唐教授在朋友家的后花园里散布，突然想通把孪生素猜想往前推进的关键一环……这中间的过程又是如何发生的？无论人脑产生的是美妙的想法，还是那种令人追悔莫及的念头，都是人的一部分意识而生。

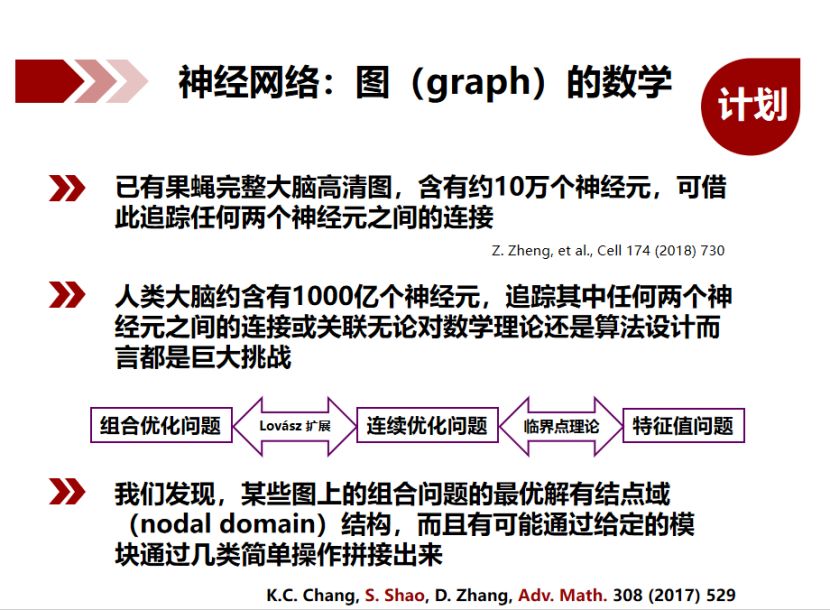
而这一切的物质基础——大脑，则是由约 1000 亿个神经元构成的脑神经网络。而组成神经元的微观粒子更是与自然界中的原子别无二致，那么该网络又是如何在在思想世界里产生意识的，是否满足量子力学的规律，所谓智能又从何而来？这个课题在学术界早有关注，但至今仍搁浅在学说阶段，一直都没有太大进展。究其原因，一言以蔽之，曰“测量难”，无论是微观世界的神经元定位，还是物理学层面去测一个对象的量子力学行为，都相当困难。

为了解答这个问题，邵嗣烘及其团队计划并展开了一系列探索，包括基于量子力学的维格纳函数的模拟，以及了解所谓的图上的数学和算法问题等，其目前已取得的主要代表性成果包括：获得了多体狄拉克波函数的渐近行为，为发展高精度相对论波函数方法提供了数学基础；发现了非线性狄拉克孤波的多峰结构，揭示了该结构会破坏稳定性，对领域的发展具有推动作用；利用维格纳方程的数学结构，设计了一类高精度数值格式，实现了四维相空间内确定性的含时计算；给出了多体维格纳方程分枝随机游走算法的数学理论，为量子动力学模拟提供了一套新的随机算法思路。

分享最后，邵嗣烘感慨道，事实上我们直到去年才有机会看到一个果蝇的脑神经元，可能是时候从根上或者从数学理论去理解人工智能的问题了，也许我们才刚刚开始……

王涵：基于深度学习的分子动力学数值方法

北京应用物理与计算数学研究所副研究员王涵

北京应用物理与计算数学研究所副研究员王涵的报告主题为《Deep Learning for Multiscale Molecular Modeling》，重点探讨了基于深度学习的分子动力学数值方法，介绍了深度学习在多尺度分子建模中独特且有趣的应用，以及过程中遇到的问题。

首先什么是分子模拟，概念非常简单，假设这个世界由原子构成，我们将每一个原子看作一个质点，然后依据牛顿运动第二定律，给定初值以后就能把这个方程解出来，从而获知所有原子在任意时刻的坐标，这就是分子模拟在做的事。但是大家如果看过《三体》，马上就会意识到这个方程要想精确求解，只能针对两原子体系，任意一个多原子体系都无法在无穷长的时间内把这个方程精确地解出来，或者说你的初值误差就会变得非常大，导致你的解完全不靠谱。

但我们想要通过分子模拟得到的并非原子运动的轨道，而是原子运动的轨道在无穷长时间内对相空间的作用。所谓相空间是什么？就是所有原子的坐标构成的一个空间。如果有 n 个原子写在一起，我们想研究这个轨道在 n 空间中的分布，在这种情况下，数值误差对这个分布的影响实际上是可以控制的。如果我们的离散做得足够好，我们得到的结果就能够和物理中想要的分布一致，这就是分子模拟一个最基本的理念，或者说是我们正在做的事情。

这里方程已经写出来了，但我们还不知道每一个原子的受力，每个原子的受力写成公式实际上就是这个能量的负梯度，能量就是依赖于所有原子的。假设一个体系里有n个原子，知道坐标后就能把体系能量写出来，同时对任意一个原子坐标求负梯度，就能知道原子的受力。我们所谓的分子建模，就是把能量函数的E给写出来。多尺度分子建模就是说对这个原子坐标做一定的粗粒化，然后怎么样写出一些等价的形式。

这里的 E 本质上是多维函数，多维函数在传统数学的手段上处理起来还是比较困难的，正好深度学习为我们处理多维函数提供了非常有利的工具，这也是我们研究的出发点。

稍微回顾一下分子建模或解能量函数E的传统方法，包括两种套路，其一是从头算，就是把体系中的电子结构给解出来，就像刚才邵老师讲的，从学薛定谔方程出发，把体系中所有电子的结构解出来，这样的话自然就获得能量函数 E。其优点在于出发的模型几乎没有任何假设，能量 E 可以解得非常精确，甚至和实验对得非常好；缺点则是非常昂贵的，典型的大家能够算得起的体系实在是太小了。另外一种套路就是经典力场建模，假设E有某种比较简单的函数形式，实际上是显式的函数形式，当然里面带了一些参数。我猜出这种函数形式，然后我去套参数，使得这个 E 尽可能的靠谱。这么做的好处当然是快，但是缺点就是精度非常有限。而我们的思路就是用深度学习去解决这个问题，我们希望达到的目标就是能够在保证第一性原理计算的精度条件下，做到计算开销和经典力场尽可能合并。

王涵及其合作者发展了基于深度学习的原子间相互作用建模方法——深度势能，提出通过模型一致性估计深度势能模型误差的方法，在本质上改善了原子间相互作用的建模精度。深度势能的模型精度达到与第一性原理计算一致，同时计算开销的阶由 O(N3) 降低到 O(N)，其中 N 为体系中原子个数。数值实验表明，在约 100 个水分子的模拟中，深度势能的计算开销比第一性原理计算节省将近 5 个数量级，极大地提高了计算效率。

英国皇家学会外籍院士 Parrinello 使用深度势能分子动力学方法研究硅的熔化，克服了传统原子间相互作用模型无法同时精确刻画硅的固相和液相的困难。北京师范大学的崔刚龙教授课题组对深度势能模型进行了扩展，用于对非绝热激发态分子动力学建模，克服了传统方法在能量面交接锥处模型精度低的难题，获得了和第一性原理一致的激发态动力学模拟结果。

张志华：“机器学习才是解决人工智能的王者之道”！

北京⼤学教授张志华

本此论坛最后一位分享嘉宾是来自北京⼤学的张志华教授，他同时还是机器学习领域顶级杂志 JMLR 的编委，国内统计学习领域的学术带头⼈。其报告题为《数学⼯程——理解机器学习的⼀种⻆度》，认为数学工程是通向人工智能的一种途径，提出从“数学⼯程”的角度来理解机器学习。

他⾸先回顾了机器学习发展的⼏个重要阶段：基于规则的学习、基于统计推理的学习、基于深度表示的学习等。同时还讨论了机器学习的四个基础原则：泛化性、稳定性、可计算性和可解释性等，并分析了解决这些问题的⼀些基本数学⼿段。

谈及此次分享，张志华坦言，他的看法和角度可能不一定是大家所公认的，但他这么多年的研究经历一直站在前沿，对机器学习、深度学习都有自己的理解。

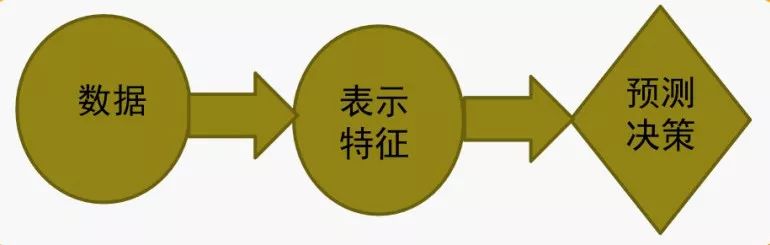
他认为机器学习与人工智能有着本质上的不同，前者志不在模拟人的思维和行为，主要是想通过经验和交互的方式改善性能，是基于规则的学习。机器学习实际上是研究算法的学科，这个算法是基于数据型算法，然后反馈到数据中去。我们可以简单地把机器学习的过程看作这样一个思路，然后可以基于此看看机器学习发展的历程：

传统方法：基于规则学习

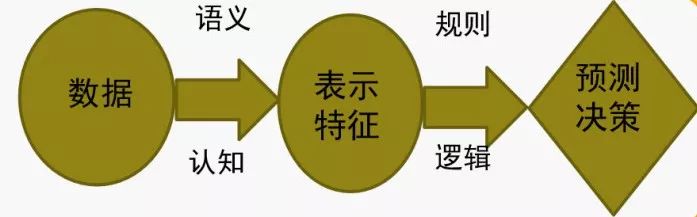
第一个比较成熟或者说比较有代表性的历程是基于规则的学习，其目的就是规则，用规则去做预测。但重点不在于怎么形成规则，而是试图把人类对目标的认知形式化表示，从而自然地形成规则推理，其代表的形态有专家系统和句法模式识别。其重点为特征工程，也就是从数据到表示，而这一过程也涉及大量深入的领域知识要求。

但这一阶段也暴露出一些问题，其一便是基于规则学习的方法虽然对于浅层推理比较有效，但遇上深层推理需求，如果形成规则过多，在其中搜索就容易出现前面的分享提到过的维数灾难问题。

为了解决这个问题，一个用一个强大的非线性学习模型来弱化数据到表示这个过程的作用，基于这样的理论，机器学习发展至第二个阶段。

统计机器学习：黄金发展十年

90 年代中期到 2005 年左右这十年，是统计机器学习发展的黄金时期。

与之相反的是，这一阶段的神经网络（80 年代就已经出现神经网络模型）则相对趋于比较低落的时期，表现平平，发展遇冷。主要原因在于这个时期的机器学习方法比神经网络要更为简单，性能也要更好，属性性质相对完美，自然而然地就取代了神经网络。

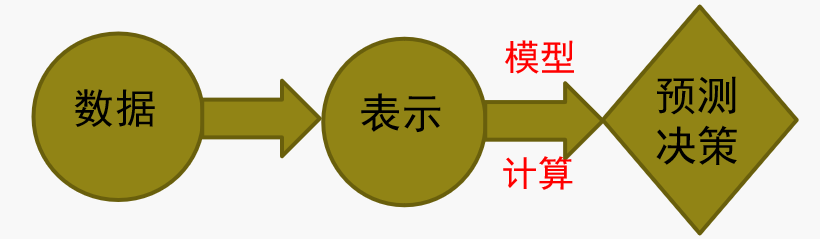
但随着这个统计方法发展到一定阶段，大家发现“数据到表示”这件事情还是绕不过去。而应对这一问题地一个简单的思路就是通过学习的途径来求解表示问题，从而弱化研究者对于领域背景高度掌握的要求，也就是通过一个自动化的方式来解决这一问题。

基于深度表示的学习

大模型+大数据+大计算使得这种思路变得可行，机器学习也进入了第三阶段。AlexNet 网络的提出在后来为这个问题带来了突破性进展，很多做计算机视觉的人在网络方面不停跟进，这些发展主要是基于视觉的。

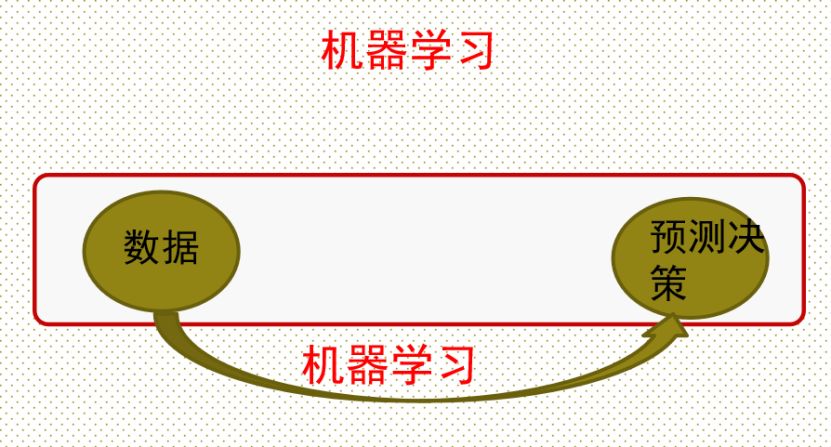
深度学习发展至今，主要是有监督的，但是现在无监督的问题远多于有监督的问题，而且还更复杂。那么一个简单的思路就是要把无监督问题形成为与有监督类似的一个学习优化过程。

张志华认为机器学习的关键在于表示学习，表示需要适合预测和适合计算。而深度表示所面临的挑战包括：由于大数据的需要可能导致过参数化；由于多层的表示，导致问题高度非凸化。而机器学习的基础原则是可预测性、可计算性、稳定性以及可解释性。

关于机器学习和数学工程间的关系，他给出了这样的阐释：

统计为求解问题提供了数据驱动的建模途径；
概率论、随机分析、微分方程、微分流形等工具可以引入来研究 AI 的数学机理；
无论从统计角度还是从数学角度来研究 AI，其实际性能最后都要通过计算呈现出来：

数值分析，即求解连续数学问题的算法；
离散算法，即求解离散结构问题的算法；
大规模计算架构。

在最后的总结中，张志华指出，现在谈数学工程，一是统计，二是数学——统计为解决问题提供了最佳建模途径；而数学里的概率论、随机分析等工具可以用来研究 AI 的数学机理。而这一切最终都将通过计算呈现。机器学习=数学+工程，应用数学最重要的魅力在于帮助我们提出解决问题的思路或途径，而不仅仅在于证明理论；工程是技术也是艺术，它是算法的必要补充，是新算法提出的源泉；机器学习是数学和工程的完美结合体现。

了解更多人工智能数理基础系列报告，请关注智源研究院公众号，紧密追踪 5 ⽉ 13 ⽇及 16 ⽇的后续论坛，另有十位顶尖学者将为大家带来精彩分享！

❖

关于主办方

北京智源人工智能研究院 （Beijing Academy of Artificial Intelligence，BAAI）是在科技部和北京市委市政府的指导和支持下，由北京市科委和海淀区政府推动成立，依托北京大学、清华大学、中国科学院、百度、小米、字节跳动、美团点评、旷视科技等北京人工智能领域优势单位共建的新型研究机构。

报名方式