基于规则的建模方法的可解释性及其发展

摘要: 建模方法的可解释性指其以可理解的方式表达实际系统行为的能力. 随着实践中对可靠性需求的不断提高, 建立出可靠且可解释的模型以增强人对实际系统的认知成为了建模的重要目标. 基于规则的建模方法可更直观地描述系统机理, 并能有效融合定量信息和定性知识实现不确定信息的灵活处理, 具有较强的建模性能. 本文从基于规则的建模方法出发, 围绕知识库、推理机和模型优化梳理了其在可解释性方面的研究, 最后进行了简要的评述和展望.

系统建模是一种简化实际工程系统的技术, 通过它可以对实际系统进行分析、预测、仿真和改进, 以满足工程应用需求[1]. 近年来, 以深度神经网络(Deep neural networks, DNN)为代表的黑箱模型由于其良好的操作性与建模精度, 在诸如人脸识别[2]、智慧医疗[3]和声纹识别[4-5]等领域中得到了广泛的应用. 然而, 黑箱模型的内部参数与结构难以被人理解, 其输出的合理性与可靠性也难以得到验证, 这从一定程度上增加了黑箱模型在实际工程应用中的潜在风险, 尤其是在如医疗诊断决策等对安全性敏感的任务中[1, 6-7]. 在工程实践中, 为了满足实际系统的高可靠性需求, 一方面是在实际系统的可靠性设计中考虑更多因素. 另一方面, 就是通过合理的建模方法建立出可靠且可理解的模型以增强人类对实际工程系统的认识, 获得系统的真实状态, 并据此采取合适的策略对实际系统进行改进和维护, 确保其安全可靠地工作[1]. 因此, 建模方法的可解释性逐渐成为了系统建模必须考虑的重要因素.

建模方法的可解释性指其以可理解的方式表达实际系统行为的能力, 它有利于提高模型的可信度. 在构建模型时, 模型的结构与表达方式清晰易理解, 能融入真实系统的设计原理与经验知识; 在推理计算时, 保持过程的合理与透明性; 在模型优化时, 保证优化后模型的上述性质不被破坏. 这些都利于建立人与模型间的信任关系, 并进一步增强人与模型之间的交互与协作[1, 8-9]. 为了提高系统建模方法的可解释性, 诸多研究人员就模型的可解释性问题开展了广泛和深入的研究, 但由于对可解释性的理解存在主观性, 目前学术界还未给出其统一的定义[1, 8-12]. 在相关研究中, 不同研究者看问题的角度不同, 赋予了“可解释性” 不同的含义, 因而所提出的可解释性方法也各有侧重.

模型的可解释性可以分为两类: 1)事后可解释性(Post-hoc可解释性), 旨在通过设计高保真的解释方法或者构建高精度的解释模型对原本可解释性弱的模型进行解释, 以可理解的方式展现其工作机制[13]. 例如, 随机森林(Random forest, RF)[14], 提升树(Boosting tree, BT)[15], DNN[2-5, 16]等模型由于参数量大, 结构复杂, 工作机制透明性低, 属于一类可解释性弱的模型. 针对这些模型, 研究人员提出包括规则提取[17-20]、模型蒸馏[21]、激活最大化[22]、敏感性分析[23-25]、特征反演[26]、类激活映射[27]等在内的一系列方法帮助人们从整体或者局部理解模型内部的复杂机理[28]. 2)事前可解释性(Ante-hoc 可解释性), 指模型本身内置的可解释性, 即无需采取额外的手段便可理解模型的工作机制. 在建模中为了实现Ante-hoc可解释性, 通常选择结构透明、易于理解的自解释模型, 例如线性回归[29]、朴素贝叶斯[30]、决策树[31]、基于规则的模型[32]等. 对于线性模型, 可以通过模型权重体现特征之间的相关关系, 并通过矩阵计算线性组合样本的特征值, 最终复现线性模型的决策过程[33]. 对于朴素贝叶斯模型, 其概率推理过程是透明可理解的[34]; 而决策树模型中, 每一条从父节点到子节点的路径都可转化为一条二分产生式规则, 形成可追溯的推理过程[35-36]. 但是单个决策树模型的建模能力较弱, 在实际工程中往往集成多个决策树构成集成学习相关方法, 其可解释性也随之降低[37]. 由于规则能够更加直观地描述和解释系统机理, 因而基于规则的建模方法(Rule-based modeling approach, RBM)在理论及应用中得到了更加广泛的认可与关注.

人工智能领域的符号主义学派强调通过逻辑来描述和模拟人的智能行为, 将知识表示系统分为四类: 1)基于逻辑的知识表示; 2)语义网络; 3)基于框架的知识表示; 4)产生式知识表示. 产生式知识表示最早来源于美国数学家 Post提出的波斯特计算模型(Post machine), 它描述的是人类思维判断中的一种固定逻辑结构关系, 即常见的“原因−结果”、“条件−结论”以及“前提−操作”等[38]. 产生式知识表示有多种可以互相转化的形式, 例如逻辑蕴含式和产生式规则. 在现有的研究中, 基于规则的建模方法中的“规则” 指的就是产生式规则. 产生式规则描述为“IF-THEN” 形式, 从Newell和Simon等开发的基于规则的产生式系统开始, 已逐渐成为了专家系统、人工智能等领域中应用最广泛的知识表示方法[1, 32]. 最初的产生式规则对确定性信息具有较为直观的描述能力. 1965年, Zadeh 在 Information and Control 杂志发表“Fuzzy sets”, 提出了一种利用模糊集合和模糊逻辑分析复杂系统的新方法[38]. 由该方法衍生的模糊规则, 如Mamdani-Larsen (ML)型规则[1, 39]及Takagi-Sugeno (TS)型规则[1, 40-41], 通过语义变量和模糊命题为系统行为的描述提供了更加易于理解的表达形式, 且更加符合人类的推理模式[32]. 在诸多领域中, 基于模糊规则的建模方法能够有效利用定量信息和定性知识处理模糊不确定性. 但是在实际工程系统中, 模糊不确定性(Fuzzy uncertainty)、不完备性(Incompleteness)、概率不确定性(Probabilistic uncertainty)等各类不确定性广泛共存, 这严重制约了模糊规则的建模性能[42-45]. 为此, Yang 等于2006年在Dempster-Shafer证据理论[46-47]、决策理论[48]、模糊理论[38]和传统产生式规则[1, 32, 38]的基础上, 将置信框架引入传统产生式规则, 提出了基于证据推理算法的置信规则库推理方法(Belief rule-base inference methodology using the evidential reasoning approach, RIMER)[42, 45]. RIMER方法的核心之一是置信规则库(Belief rule base, BRB), 它是传统模糊规则库(Fuzzy rule base, FRB)的一般化, 能为工程系统中知识提供更加可靠的描述[45].

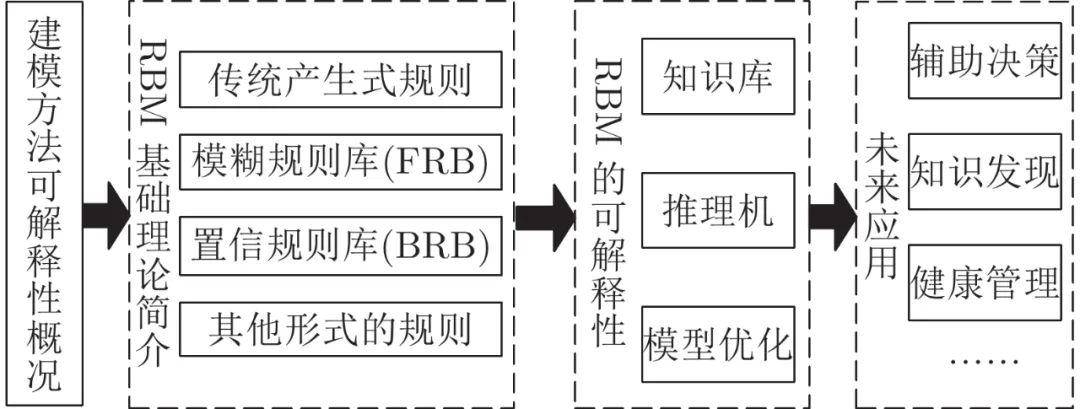
RBM的优势在于其内置的可解释性, 本文的“可解释性” 侧重于说明如何建立和保持RBM的内置可解释性, 即如何在构建知识库时获得可解释性, 如何保证推理过程的透明可解释, 如何在优化过程中保持可解释性. RBM的可解释性主要取决于几个因素, 包括模型结构、规则数目、模糊集的形状等[8, 10, 45]. Zhou等结合前人的研究从模糊集和模糊规则层面将FRB的可解释性分为低级可解释性(Low-level interpretability)和高级可解释性(High-level interpretability)[10]. 然而, 随着模糊规则被拓展为置信规则, 高低级可解释性在描述BRB系统的可解释性方面存在一定的局限性. 本文主要对RBM的发展进行概述, 从知识库、推理机、模型优化等角度分析总结典型文献中关于其可解释性的研究, 并在此基础上对其未来发展进行了阐述, 旨在为RBM的发展和改进提供一定的参考和借鉴. 本文的整体框架如图 1 所示.

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“规则可解释” 就可以获取《基于规则的建模方法的可解释性及其发展》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源