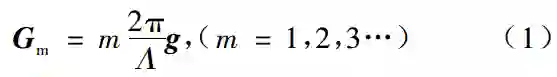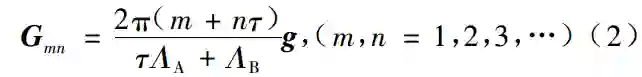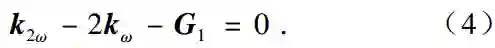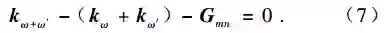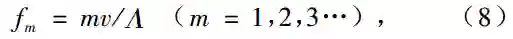介电体超晶格的研究 | 闵乃本

2018 年 9 月 18 日 中国物理学会期刊网

作者：闵乃本朱永元祝世宁陆亚林陆延青陈延峰王振林王慧田何京良（南京大学固体微结构物理国家重点实验室）

1 引言

半导体晶体中存在电子能带，通过能带设计与裁剪，实现了电子调控，奠定了当代信息技术的基础. 然而，光子能带不存在于均匀晶体中.

上世纪 70年代，将周期微结构引入半导体晶体，构成半导体超晶格. 在这一成就的启发下，我们于上世纪 80年代初，将微结构引入介电晶体，构成介电体超晶格. 超晶格的周期可和光波、超声波的波长比拟. 光波、超声波在介电体超晶格中传播，就类似于电子在晶格周期势场中运动. 于是，光子能带、声子能带及其他准粒子能带就出现在介电体超晶格中.

介电体中引入有序微结构，可以实现不同物理常数的有序调制. 介电常数（或折射率）周期调制的介电体超晶格，称为光子晶体，具有光子能带.弹性常数周期调制的称为声子晶体，具有声子能带. 压电常数周期调制的称为离子型声子晶体（ionic-type phononic crystals），具有极化激元能带. 非线性光学常数被调制的称为准位相匹配材料（quasi-phase-matching materials），在激光变频方面有着广泛的应用.

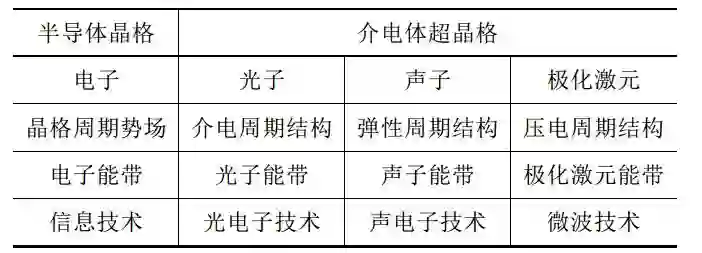
表 1 介电体超晶格与粒子或准粒子能带

表1列举出半导体晶格和介电体超晶格所具有的不同粒子（如电子和光子）、准粒子（如声子和极化激元）能带，周期结构的类型以及可能的应用领域. 我们期待介电体超晶格能像半导体超晶格一样，通过不同能带的设计、裁剪，实现粒子、准粒子的调控，对光电子技术、声电子技术以及微波技术作出贡献.

1984年发现了准晶. 1986年我们将准周期引入介电体超晶格. 周期超晶格只有一组倒格矢，只能高效完成一个光参量过程. 准周期超晶格具有多组倒格矢，能同时高效完成多个光参量过程. 我们于1990年建立了多重准位相匹配理论. 1995年发展了能够制备准周期介电体超晶格的室温电场极化技术. 1997年完成了实验验证，将两个光参量过程高效地集成于一块准周期超晶格之中，实现了两种波长激光同时输出. 2003年实验上实现了超晶格中三基色的产生. 2005年研制成超晶格三基色和白光全固态激光器原型. 此外，在光散射的准位相匹配增强效应、高频超声激发、微波与超晶格振动耦合等方面也有所发现.

从真空电子管到半导体场效应晶体管，实质上是将电子发射、电子调控、电子收集诸过程，全固态地集成于半导体微结构中. 这一全固态集成，使实现电子调控所需空间缩小了约7.2x10¹³倍，这为集成电路四十多年来能按莫尔定律发展提供了可能. 我们关注于光电子学中的类似的全固态集成，如上所述，将多个光参量过程集成于一块介电体超晶格之中，这只是第一步. 将不同的物理过程（如变频、会聚、偏转、开关等）集成于一块有序微结构材料之中，是我们的努力目标.

2 介电体超晶格的组成、制备与表征

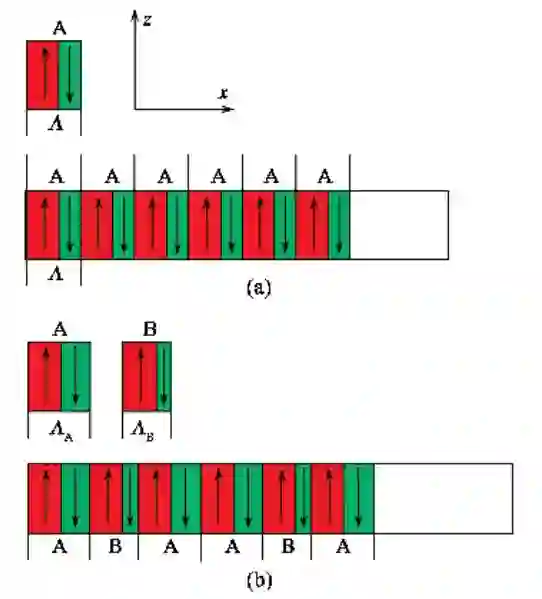
介电体超晶格的组成：以有序铁电畴为例，简要说明介电体超晶格的组成. 属 3m点群的铌酸锂（LiNbO₃, LN）、钽酸锂（LiTaO₃, LT）铁电晶体中，铁电畴自发极化矢量，或是平行于 ! 轴（正畴），或是反平行于z轴（负畴）. 取一对正、负畴作为构造单元. 如果取一种构造单元重复排列，这就构成了周期超晶格，如图 1（a）所示. 如果取二种构造单元按 Fibonacci序列排列，这就构成了二单元 Fibonacci准周期超晶格，如图 1（b）所示. 通常用倒格矢来描述晶格或超晶格. 对周期超晶格，其倒格矢可表示为

式中Λ为超晶格结构参量，即超晶格周期， g是G_m的单位矢量，垂直于畴界，见图 1（a）. 当m=1, G1=2πg/Λ为超晶格的初基倒格矢. 在光参量过程中，使用初基倒格矢，其转换效率最高. 对二单元Fibonacci准周期超晶格，其倒格矢可表示为

其中 τ=1+√5/2为黄金分割数，Λ_A和Λ_B是超晶格结构参量， g为G_mn的单位矢量，垂直于畴界，见图 1（b）. 可以看出，设计准周期超晶格，有更多的结构参量可调，更多的倒格矢可选用. 因而在一块准周期超晶格中，可以同时高效地实现多个光参量过程. 从理论和实验方面研究了二单元 Fibonacci准周期超晶格的超声激发谱、激光倍频谱和电光透射谱. 发现了超声谱结构的自相似性，这是实空间结构自相似性在倒空间中的反映. 而激光倍频谱和电光透射谱，由于折射率的色散效应，谱结构的自相似性遭到破坏. 最近还研究了极化激元的色散谱和介电谱，都得到了理论与实验相符的结果. 对二构造单元按 intergrowth序列和按Thue-Morse序列，三构造单元按准周期序列构成的超晶格，以及双周期、非周期超晶格都进行了系统的研究. 在此基础上建立了设计介电体超晶格的专家系统，己能按需优化设计介电体格超晶格.

图1 超晶格的构造（a）一种构造单元（A）无限重复就构成周期超晶格；（b）两种构造单元（A 和 B）按 Fibonacci序列就构成准周期超晶格

通过构造单元的有序排列，实现了铁电畴自发极化矢量的调制. 现在简要说明，如何通过铁电畴自发极化矢量的调制实现物性常数的调制. 从图 1（a）可以看出，构造单元是由一对正畴、负畴组成，其自发极化矢量相反. 其中负畴的形成可想象为，将原为正畴的第二片及描述物性张量坐标系的z轴，绕x轴相对于第一片旋转180°，故第二片畴中奇数阶张量变号，而偶数阶张量将保持不变. 因而在这类超晶格中，对应的三阶张量的如非线性光学常数、电光常数、压电常数不再保持不变，而是空间坐标的函数，属二阶张量的介电常数和属四阶张量的弹性常数在整个超晶格中保持不变.

介电体超晶格的制备：如何实现铁电畴自发极化矢量的有序调制，我们发展了两种技术，就是生长层技术和室温电场极化技术. 前者用于制备周期性超晶格，后者用于制备周期、非周期以及二维超晶格.

晶体生长过程中，如果出现周期性温度起伏，就出现周期性生长层，就如树木生长中出现的年轮. 周期性生长层是晶体（固溶体）中溶质浓度沿生长方向的周期性分布. 通常溶质以离子状态存在于晶体中，周期性溶质分布就等价于周期性空间电荷分布，于是在晶体中产生了周期性内电场. 在降温过程中，当温度通过居里点时，即从顺电相向铁电相转变时，该内电场将引起金属氧化物晶体（如LN，LT）中在顺电相处于对称中心的金属离子（如 Nb， Ta）沿z轴的正向或反向的择优位移，这就决定了这类晶体中铁电畴自发极化取向. 于是在晶体生长过程中，人为地引入周期性温度起伏，通过周期性生长层的产生，实现了铁电畴自发极化矢量的周期调制，并发展成制备周期超晶格的生长层技术.

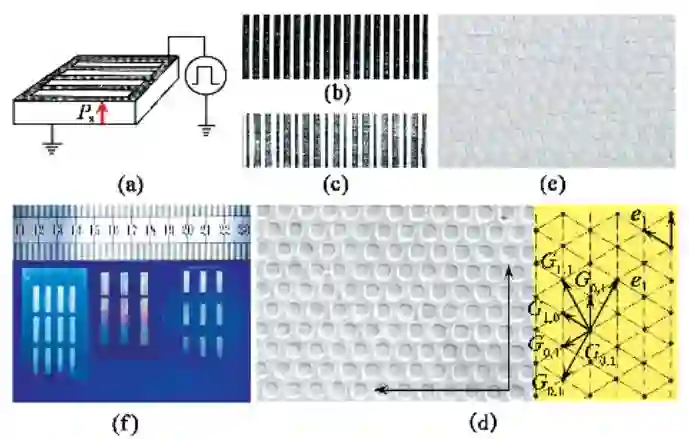
为了制备准周期超晶格，借用半导体平面工艺.取一片z切割的单畴LN或 LT晶片，在其上、下晶面沉积金属膜作为电极. 下晶面的金属膜为平面电极，上晶面的金属膜通过半导体平面工艺刻蚀成具有周期、准周期、或其他有序图案的电极，二电极与高压脉冲发生器联结，如图2（a）所示（图中 Ps为自变极化矢量）. 在高压脉冲电场作用下，单畴晶片中的反向畴首先成核于上电极界面处，逐步向下延伸. 适当选择脉冲强度、脉冲宽度和脉冲重复频率，可使反向畴贯穿整个样品，获得与图案电极相同的有序畴结构. 这被称为室温电场极化技术. 图 2（b），（c）和（d）是用该技术制备的周期、准周期和二维周期超晶格，图 2（e）是具有特定图案的有序畴结构. 该技术能用于批量生产，图 2（f）表明晶片上同时制备的多个相同和不同的超晶格.

图2 制备超晶格的室温电场极化技术（a）室温电场极化装置；（b）周期超晶格；（c）准周期超晶格；（d）二维周期超晶格；（e）二维有序畴结构；（f）超晶体的批量制备

介电体超晶格的表征：为了实现对介电体超晶格的无损检测，我们发展了两种表征技术，即介电常数与介电损耗的微波近场显微成像技术，以及环境扫描二次电子成像技术.

通常，可方便地测得体块材料的介电常数与介电损耗，我们更关心局域表征. 我们发展了介电常数与介电损耗的微波近场显微成像技术，其分辨率达亚微米量级. 我们知道，介电极化来源于电子极化和离子（位移）极化. 在光频波段只有电子极化作出贡献，而在微波波段二者都有贡献. 因此在微波波段，近场显微像能提供更多的信息. 通常复介电常数可表示为

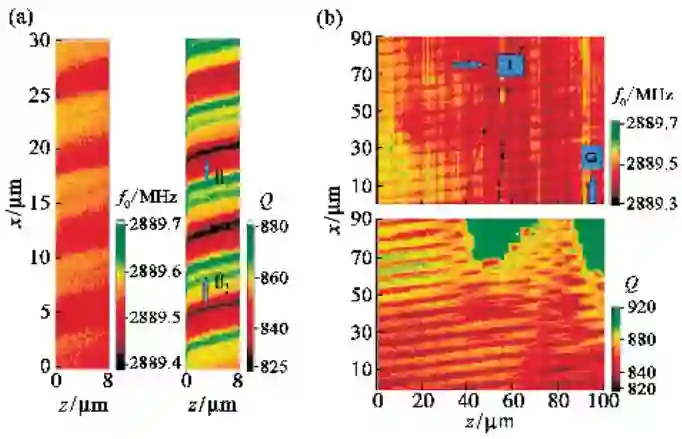
其中实部ε'为介电常数，虚部ε''为介电损耗. 系统的共振频率为 f₀，有∆f₀/f₀=g∆ε'，其中常数g=∽7.1×10^-5（给定实验系统的测量值），故共振频率像反映了介电常数的变化，因而能反映晶体中的掺杂浓度和内应力，参阅图3（a）的左图. 系统的品质因子为（1/Q），有 ∆(1/Q)=g'∆ε''，其中g'=∽7.1×10^-2，品质因子像反映了介电损耗（微波吸收）的空间变化，与微波作用下的离子位移和畴界振动有关，显然，畴界处介电损耗最大，参阅图3（b）的右图. 图3（b）对比了 LN超晶格的同一区域的两种像，上图为介电常数像，下图为介电损耗像. 可以看出，在该区域的右上部，介电常数像（上图）与介电损耗像（下图）中的周期结构遭到破坏，在介电损耗像（下图）中出现绿色区（其介电损耗最大），这对应于岛屿畴分布区. 岛屿畴区内畴界密度较大，因而介电损耗亦大. 岛屿畴区的出现是晶体生长过程中界面失稳所致. 微波近场显微术不仅能表征超晶格中的周期畴结构，还能提供超晶格中的溶质分布、内应力分布、双折射的均匀性以及微波吸收分布的有关信息.

图3 介电常数与介电损耗的微波近场显微成像. （a）左为介电常数像，右为介电损耗像；（b）同一区域的两种像，其中上部为介电常数像，下部为介电损耗像

介电材料通常都是绝缘体，用电镜观察时，入射电子束在绝缘体表面形成电荷积累，使电子像逐渐模糊. 通常必须在表面蒸镀导电膜，以防止电荷积累. 近年来，环境扫描电镜的发展，有可能直接观察绝缘样品而不需表面导电膜. 这是由于环境扫描电镜腔内的气压较通常扫描电镜内高一万倍，利用入射电子束与中性分子碰撞产生的自由离子，在样品表面邻近形成的通道，来消除表面电荷积累. 另一方面，二次电子成像技术的发展，能使不作任何处理（如浸蚀）的表面直接成像. 我们在环境扫描电镜中，在未作处理的 LT超晶格表面，实现了周期铁电畴的二次电子成像，而且图像稳定，与传统方法获得的像相符.

3 介电体超晶格的光学效应

介电体以介电极化为特征，介电极化来源于电子极化和离子（位移）极化. 在光频波段离子的位移跟不上光波的变化，因此只有电子极化作出贡献. 这里考虑二阶非线性极化. 当共线的频率为 ω₁ 和 ω₂的光作用于非线性介质时，引起的二阶非线性极化强度含有2ω₁，2ω₂， ω₁±ω₂ 等不同频率分量，相应的极化分量将辐射上述频率分量的光波. 但要获得这些频率分量的有效输出，其相应的光参量过程必须满足能量守恒和动量守恒. 以和频为例，为了使能量有效地从频率为ω₁和 ω₂的基波光转换到频率为ω₃的和频光，必须满足的能量守恒为ω₃=ω₁+ω₂和动量守恒为 k₃=k₁+k₂，或 k₃-(k₁+k₂)=0. 其中k_i=n(ω_i)/c ω_iκ，（i=1,2,3）， k_i是频率为 ω_i的光的波矢，κ是 k_i的单位矢量，三波矢是共线的. 这里动量守恒用波矢量守恒表达，通常称为位相匹配. 若ω₁=ω₂=ω，即 k_ω1=k_ω2=k_ω，由能量守恒，有 ω₃=2ω，由波矢量守恒，即k₂_ω-k_{_ω}=0，有 n(2ω)=n(ω)，此为倍频情况. 可以看出，位相匹配要求基波光与倍频光的折射率相等，亦即要求在介质中基波光与倍频光的相速度相等. 然而由于折射率色散效应，n(2ω)≠n(ω)，必然产生位相失配. 利用晶体的双折射效应，在特定的方向上可以实现基波光和倍频光的相速度相等，从而得到高效输出. 这就是光学工程中通常使用的位相匹配技术.

3.1 准位相匹配

1962年， Bloembergen提出的准位相匹配理论指出，在任何光参量过程中，由于折射率色散所引起的波矢量失配（位相失配），可用超晶格提供的倒格矢来补偿. 例如，倍频过程，其折射率色散引起波矢量失配为 ∆k=k₂_ω-k_{_ω}=2ω/c [n(2ω)-n(ω)]κ，设计周期超晶格，使其初基倒格矢G₁=∆k=2ω/c [n(2ω)-n(ω)]κ，故有

(4)式被满足，即准位相匹配的条件被满足. 此时，周期超晶格的所有构造单元产生的倍频光都满足相长干涉，其振幅相互叠加，而其强度比例于叠加振幅的平方. 若周期超晶格的构造单元数（周期数）为N，构造单元产生的倍频光强为I₀，则超晶格的倍频输出为I_2ω=I₀N². 我们曾用实验定量地验证了上述结果的正确性. 对给定的光参量过程，设计超晶格，使其倒格矢与失配矢量的矢量和为零，这样就能使准位相匹配条件被满足. 这不仅对诸波矢共线的光参量过程是如此，对诸波矢非共线的光参量过程也是如此.

3.2 多重准位相匹配

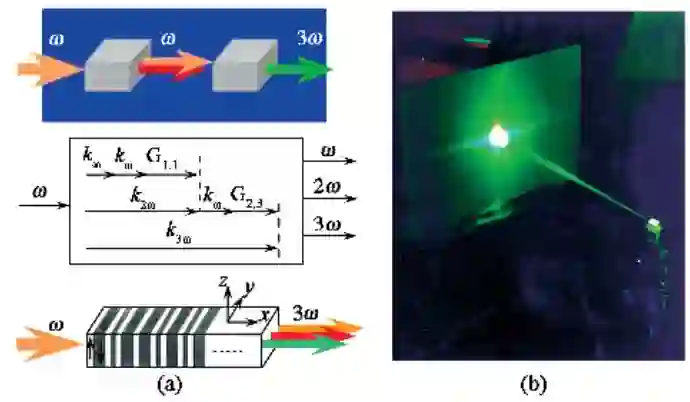
我们仍考虑二阶非线性极化. 如上所述，当二共线的频率为 ω₁ 和 ω₂ 的光作用于非线性介质，引起的二阶非线性极化强度含有 2ω₁，2ω₂，ω₁±ω₂频率分量. 如考虑一次级联效应，还存在 3ω₁，3ω₂，2ω₂±ω₁，2ω₁±ω₂ 的频率分量. 相应的极化分量将辐射上述频率的光波. 这些频率分量是通过级联光参量过程产生的. 要获得上述频率分量的有效输出，级联的诸参量过程的动量守恒必须同时满足，这对传统的位相匹配技术是不可能的，即使对上述准位相匹配技术也是不可能的. 我们于 1990年将周期超晶格拓展为准周期超晶格，建立了多重准位相匹配理论. 结果表明，准周期超晶格可提供多个倒格矢，分别参与相互级联的，或相互独立的多个光参量过程，能同时实现多个光参量过程的准位相匹配，获得多波长激光同时输出. 如果 ω₁=ω_₂=ω，上述一次级联效应产生的六种频率分量退化为一种，即三倍频3ω. 三倍频是通过抽运光ω的倍频产生 2ω，接着再与基波光 ω和频产生3ω. 这就是说，三倍频是通过倍频与和频的级联过程产生的，参阅图 4（a）. 要获得高效三倍频输出，必须同时满足倍频、和频的准位相匹配条件. 设计准周期超晶格，使之具有两个特定的倒格矢G₁₁和G₂₃，分别等于倍频与和频过程的失配矢量，于是有

（5）式和（6）式分别是倍频与和频过程的准位相匹配条件. 在准周期超晶格中，（5）式、（6）式同时被满足，级联过程得以实现，可直接得到高效三倍频输出.

图4 多重准位相匹配理论及实验（a）多重准位相匹配示意图；（b）三倍频实验

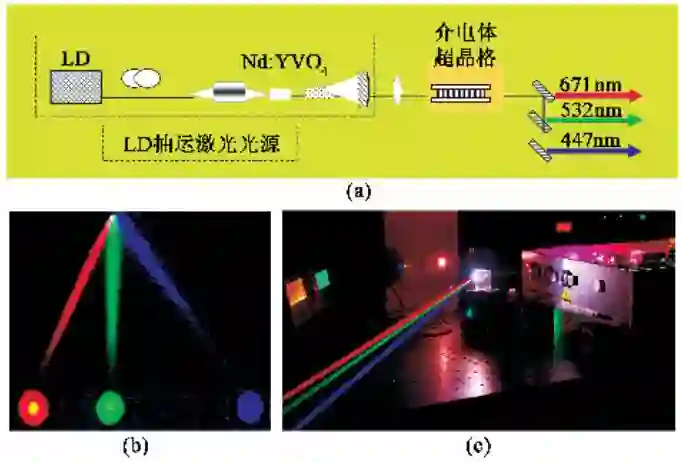
我们于 1997年实现了上述级联过程，直接得到了三倍频，转换效率为23% ，同时还获得了倍频输出，转换效率为 20% ，参阅图 4（b）. 在此基础上，通过基波（λ=1342nm）的倍频得到红光，三倍频得到蓝光，实现了红-蓝双波长激光输出. 进一步研制成红-蓝双波长全固态激光器原型，其红光输出为 1W、蓝光输出为140mW. 全固态激光技术的发展，在激光晶体Nd:YVO4中实现了波长1342nm和1064nm的同时振荡. 通过它们的倍频、和频、三倍频等就能得到多波长同时输出. 我们通过1342nm基波光的倍频得到红光、通过1342nm和 1064nm的和频得到黄光、通过1064nm的倍频得到绿光，实现了红-黄-绿三波长的同时输出. 我们还实现了红-黄-绿-蓝四波长的同时输出.

3.3 三基色与白光激光器

在上述工作基础上，我们采用了两种方案，实现了红、绿、蓝三基色同时输出，并研制成全固态准白光激光器原型. 第一方案是，用半导体抽运的掺Nd³⁺激光晶体双波长激光器作为基波光源，通过对其1342nm输出的倍频得到红光，对其1064nm输出的倍频得到绿光，对其1342nm输出的三倍频得到蓝光，见图 5（a）. 通过三基色的能量分配得到了准白光，其功率大于1W，并进一步研制成全固态三基色准白光激光器原型，参阅图5（b）和（c）. 第二方案是，以 λ_P=532nm的绿光为抽运光，通过OPO 产生 λ_s=633nm 的信号光（红光）和λ_i=3342nm 的闭置光，再由抽运光与闭置光和频产生λ_P+i=459nm的蓝光，其转换效率大于30%. 该方案的理论转换效率可达100% . 有望获得高功率白光.第二方案涉及频率下转换，可能赋于白光全新的纠缠态的特性.

图5 超晶格三基色全固态激光器（a）三基色激光器示意图；（b）实验观测结果；（c）三基色全固态激光器实物图

上面讨论的是一次级联效应和频率上转换. 在激光与非线性介质交互作用时，高次级联效应同样存在，通过上述理论与技术，可以得到高阶谐波的有效输出，如四倍频等. 频率下转换同样要求能量守恒和动量守恒，多重准位相匹配理论与技术同样有效，这就为研制量子通信的光源提供了新途径.

3.4 二维周期超晶格

我们研究了两种二维周期超晶格. 其一为铁电畴反转构成，具有二维六方对称性，在其中实现了非共线准位相匹配，获得了弹性散射和非弹性散射（拉曼散射）的准位相匹配的增强. 其二是折射率二维周期调制的，具有二维正方对称性，在其中发现新的光学双稳机制，并实现了多束光同时进入双稳态. 铁电畴反转构成的二维超晶格，其点阵参数为a=9.05 μm，初基倒格矢为垂直于密排方向的G₀₁的六个等效矢量，其大小为 4π/√3 a，参阅图 2（d）. 若入射波矢k_ω沿LT晶体的x轴，当入射波长为 1064nm时，在屏幕上出现的是其倍频光的圆环，环的中心是 k_ω在屏幕上的投影点，见图6（a）. 当入射波长为 933nm，在屏幕上为倍频光的具有镜面对称的双环，如图 6（c）所示. 若入射波矢k_ω沿LT晶体的 y 轴，随着入射光频率的变化，在投影屏上出现的倍频图样如图 6（d）、（e）、（f）所示. 详细分析表明，这是来自基波光的弹性散射导致的非共线准位相匹配倍频增强效应. 在非线性介质中，入射光与散射光的和频ω+ω'是普遍存在的. 在通常情况下，该参量过程无法满足波矢量守恒，其效应过于微弱. 弹性散射满足能量守恒，故入射光与散射光频率相等，ω=ω'，弹性散射波矢与入射光波矢大小相等，有|k_ω|+|k_ω'| . 但入射光波矢的方向是给定的，而弹性散射波矢沿所有可能的方向. 其中只有那些满足准位相匹配条件的散射波矢，才能与入射光和频得到增强. 其准位相匹配条件是，诸非共线矢量k_ω，k_ω'，k_ω+ω'与倒格矢G_mn的矢量和为零，即

如果入射波矢平行于 LT 晶体的x轴，入射波长为1064nm，初基倒格矢 G₀₁参与准位相匹配，其准位相匹配条件为k₂_ω-(k_ω+k_ω')-G₀₁=0，满足上述条件的诸波矢k₂_ω的集合，构成了半顶角为θ 的圆锥面，见图 6（b）. 因而在屏幕上的投影为一圆，见图 6（a）. 如果入射波矢平行于 LT晶体的x轴，入射光的波长为 933nm，一对镜面对称的非初基倒格矢G₁₁参与准位相匹配，在屏幕上的投影是一对具有镜面对称的双环，参阅图 6（c）. 值得注意的是，初基倒格矢 G₁₀和非初基倒格矢G₁₁及其相应的等效倒格矢，都镜面对称地分布在 y轴两侧，而沿 y轴不存在初基倒格矢，见图2（d）. 如果入射波矢平行于 LT 晶体的 y 轴，一对初基倒格矢 G₁₀参与准位相匹配，或一对初基倒格矢 G₁₀和一对非初基倒格矢 G₁₁同时参与准位相匹配，其倍频光在屏幕上的投影如图 6（d），（e），（f）所示. 关于非弹性散射，我们仔细研究了拉曼散射，证实了同样存在准位相匹配增强效应，并通过实验将散射强度提高了 10⁴-10⁵倍. 这就为设计新型拉曼激光器和发展高分辨拉曼谱学提供了新途径.

图 6 LT晶体二维铁电畴超晶格中的弹性散射和拉曼散射的准位相匹配增强效应（a）-（f）是弹性散射的增强效应，其中（a）-（c）是入射光平行于LT 晶体的 x轴，（d）-（f）是入射光平行于LT晶体的 y轴，（g）为拉曼散射增强效应

研究的第二类是折射率被调制的二维周期超晶格，具有二维正方对称性. 设计超晶格时调节其点阵面间距，对给定的入射光，使相互正交的两组点阵面都满足 Bragg条件. 因此二维超晶格内有4个Floquet-Bloch波被激发. 于是我们发展了四波动力学理论. 进一步考虑了Kerr 型介电非线性，发现了一种新的光学双稳机制，称之为折射率调制机制，观测到四束出射光同时达到光学双稳态，并对非Bragg条件下普适的多波动力学行为进行了系统的研究.

4. 介电体超晶格的声学效应

前面己经说明，在以一对正、负畴为构造单元所构成的超晶格中，相邻铁电畴的压电常数变号，即畴界处压电常数不连续. 我们知道，压电应力是压电常数与电场强度的乘积. 在恒稳电场中，畴界两侧的正、负畴内的压电应力不等（符号相反），故畴界处产生内应力. 在交变电场中，畴界处产生交变内应力. 交变内应力则产生交变应变，并以弹性波的形式在超晶格中传播，故超晶格中的畴界都可看为 δ声源. 在考虑超声激发与传播时，超晶格本身可以看为周期排列的一列 δ声源，这类超晶格我们称为声学超晶格（acoustic superlattice）. 设计声学超晶格时，适当选择相邻δ声源的间距，使所有δ声源产生的超声波相长干涉，即相干叠加. 满足相长干涉的诸δ 声源，产生的超声波的振幅相互叠加，而其强度比例于总振幅的平方. 若构造单元中δ声源所激发的超声强度为 I₀，超晶格周期数为N，该超晶格产生的超声波强度为I_n=I₀N². 通常超声工程中超声换能器都是用均质晶片制成的，可以看出，用声学超晶格研制的换能器明显地提高了超声强度和转换效率. 通过求解声学超晶格的弹性波波动方程，可得声学超晶格的电抗，从而得到谐振器、换能器的谐振频率为

其中 v是固体中声速，Λ是超晶格周期，参阅图1（a）. 值得注意的是，谐振频率只决定于超晶格周期Λ，而与晶片的总厚度无关. 如我们所知，如果用通常均质材料来制备工作频率为几百兆周到几千兆周的体波超声器件，其晶片总厚度要减薄到几十微米到几微米，对当前超声工程中的工艺系统是有困难的. 然而制备周期为数微米的声学超晶格是很方便的. 另一方面，通过求解声学超晶格的弹性波波动方程，所得换能器的电抗是超晶格周期数N 和电极面积 A 的函数. 用通常均质材料制备换能器，电抗只是电极面积 A的函数. 我们知道，在高频下静态电容是电抗的主要部分，因而换能器的插入损耗很高. 但若使用超晶格，适当地选用 N 和A，可使电抗的实部等于甚至大于虚部. 这样，换能器的插入损耗在50Ω 的测量系统中可接近于零. 我们利用声学超晶格的上述优点，研制成或提供了超声换能器、谐振器、声光偏转器、集成声开关的原型器件和设计原理，填补了当前超声工程中体波声学器件从几百兆周到儿千兆周的空白频段.

5 超晶格振动与微波耦合以及极化激元激发

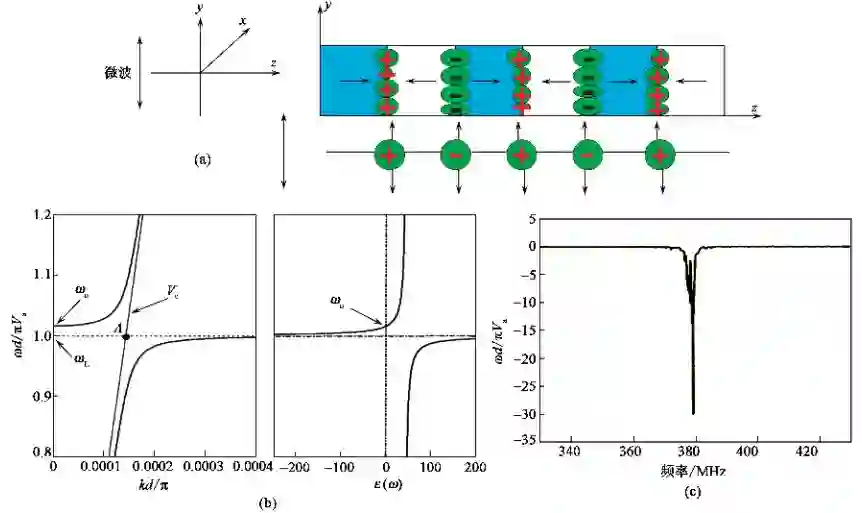
在 LT，LN这类晶体中，铁电畴自发极化矢量只能平行或反平行于 z轴，因而超晶格中存在两类典型畴界：一类是平行于z轴的畴界，如图1 所示，在畴界上不存在束缚电荷；另一类是垂直z轴的畴界，如图 7（a）所示，畴界上存在束缚电荷，且其面密度最大. 我们先讨论第二种情况，如图 7（a）所示，畴界上存有束缚电荷，且相邻畴界束缚电荷的符号相反.这样，畴界既可看为电荷中心，又可看为质量中心，于是，近似地将这类超晶格看为一维正、负离子链，如图 7（a）所示. 若 y偏振的电磁波沿 . 轴通过超晶格，将引起畴界（束缚电荷）沿 z 方向振动，这就是说，电磁波激发了超晶格振动. 反之，畴界（束缚电荷）沿y方向振动，将激发沿z轴传播沿y 偏振的电磁波. 这表明超晶格振动与电磁波耦合，并导致极化激元的产生. 这十分类似于1951年黄昆先生提出的离子晶体中电磁波与晶格振动的格波互相耦合形成的极化激元，因而我们将这类超晶格称为离子型声子晶体. 我们研究了离子型声子晶体中相邻畴界的运动规律，发现它满足的运动方程与反映离子晶体中正负离子相对运动的黄昆方程在形式上完全一样. 所得的色散曲线和介电函数曲线完全类似，参阅图 7（b）（图中ω₀为介电函数的零点频率， ω_L为超晶格中纵声波的谐振频率， V_c为尚未与超晶格振动耦合的微波波速），还得到了完全类似的联系纵、横光学波频率的Lyddane-Sachs-Teller关系式. 只不过在离子晶体中上述长波光学性质是发生在红外波段，这里发生在微波波段. 同时，我们在实验上发现了由于极化激元激发而引起的强烈的微波吸收（见图 7（c）），也就是说发现了微波吸收的新机制.

图 7 微波与超晶格振动耦合. （a）离子型声子晶体示意图；（b）极化激元的色散与介电异常；（c）极化激元激发引起的微波吸收

进一步研究发现，畴界上是否存在束缚电荷，并非产生超晶格振动与微波耦合的根本原因，其根本原因在于压电效应，在于超晶格中压电系数的周期跃变. 我们考虑如图 a（a）所示的超晶格，可以看到，超晶格中畴界上不存在束缚电荷. 在前面讨论超晶格的声学效应时，己经说明，超晶格中畴界处压电系数变号，因而可将畴界看为δ 声源，故在微波的交变电场中必然产生超晶格振动. 另一方面，在超晶格振动时，由于正、负畴中应变的符号相反，通过压电效应产生的感生极化矢量在正负畴中方向相同，在同一瞬间超晶格中所有畴的感生极化矢量方向相同，于是超晶格振动引起感生极化矢量振动，从而引起微波激发. 这就是说，由于压电效应产生了微波与超晶格振动的耦合. 基于超晶格的压电效应可以得出，不仅畴界的横振动可与微波耦合，畴界的纵振动也可与微波耦合导致极化激元激发. 这是由于畴界的纵振动通过压电效应产生横向感生极化矢量振动的原故，在实验上测量了纵振动与微波耦合产生的极化激元带隙的中心频率与带宽，其结果与理论估计相符. 我们还发现了两种不同偏振态的微波耦合而产生两类极化激元的新效应. 参阅图1（a），若y偏振的微波在超晶格中沿 x方向播，通过压电效应，激发畴界沿 x方向振动，从而产生沿 x方向传播的纵超声波. 沿 x方向传播的纵超声波通过压电效应不仅产生y偏振沿 x方向传播的微波，还同时产生z 偏振沿 z方向传播的微波. y偏振和 z 偏振的电磁波的耦合，引起了介电椭球主轴的旋转. 在这种情况下，出现了两类极化激元，一种不能通过带隙，称寻常极化激元（ordinary polariton），另一种能通过带隙，称异常极化激元（extraordinary polariton）. 这一有趣的发现，对进一步通过极化激元能带设计与裁剪，实现极化激元调控，以及研制新型的微波器件，可能具有十分重要的意义.

6 结束语

二十多年的理论与实验研究表明，介电体超晶格己经成为一种具有重要应用前景的人工有序微结构材料. 在我们对铁电畴超晶格研究的基础上，准位相匹配材料己经成为国际热门领域，以及在光电子学、声电子学、材料科学的交叉领域中催生了称之为“畴工程学”的新生学科. 实践表明，已能将多个光参量过程、平行光束的汇聚过程（透镜功能）和偏转过程（棱镜功能）集成于一块有序畴结构材料之中. 相信随着工作的持续深入，在粒子（如光子）、准粒子（如声子、极化激元、表面等离激元等）能带设计、裁剪方面，在实现上述粒子、准粒子调控方面，在级联物理过程全固态集成方面，必将对未来光电子技术、声电子技术、微波技术的发展作出贡献.

本文选自《物理》2008年第1期

十大热门文章

8. 忆阻器研究新进展：基于二维材料的可耐受超高温忆阻器

9. 寂静春天里的动力学（上）

10. 一种充满惊喜的二维材料