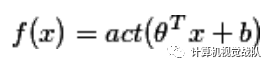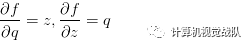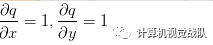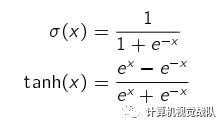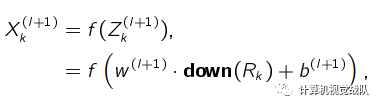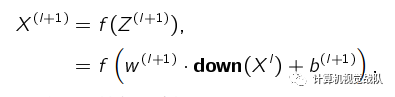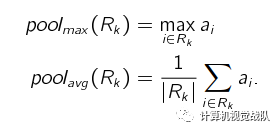CNN的全面解析(带你简单轻松入门)
亲爱的关注者您好!真的是好久不见,上次与您相见还是8月18日的晚上,不知道35天的时间不见,你们都有了哪些成果?有了哪些成就?有了哪些offer?但是,本平台的所有学生工作者祝您前程似锦。
今天主要给大家详细说说深度学习的基础知识——卷积神经网络。这不是刚开学不久,绝对又有一大批同学选择进入计算机视觉领域。所以今天主要的内容是想让刚入门或想入门的您有一个简单轻松的入门方式(有兴趣或附近朋友想加入这个领域,欢迎他关注我们的平台,加入我们的学习群,谢谢!),希望可以给您带来一丝丝帮助,也希望给已经入门的您回归下基本知识,当作科研后的歇息放松的一种方式。谢谢大家的支持。
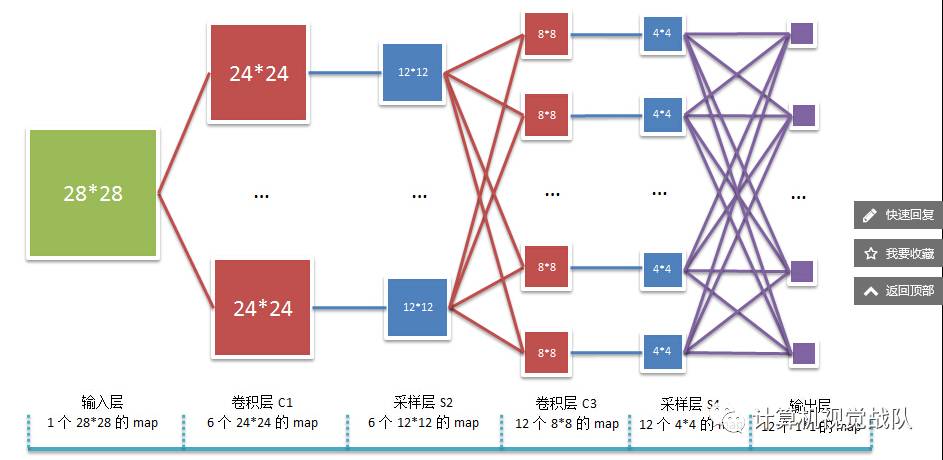
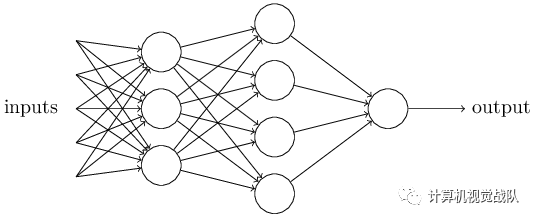
卷积神经网络沿用了多层感知器的结构,是一个前馈网络。在语音和图像领域有很好的应用,大体主要结构如图1所示。
1、输入层:
一般使用RGB彩色图像,此时输入图像有三张,分别为RGB分量。
2、卷积层(C)和下采样层(S):
将上一层的输出与本层权重W卷积得到各个C层,然后下采样得到各个S层。一般会使用激活函数,如果使用Sigmoid激活函数,则归一化到[0, 1],如果使用tanh激活函数,则归一化到[1, 1]。这些层的输出称为Feature Map。
3、全连接层(FC):
将上一层的所有Feature Map的每个元素依次展开,排成一列。
4、输出层:
最后的分类器一般使用Softmax,如果是二分类,当然也可以使用LR。
如果要深入理解CNN,现在开始从感知器开始学习。
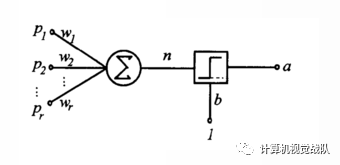
感知器
深入学习可阅读此文章:每日一学——卷积神经网络
模型:
其中 act 为激活函数,可以使用{sign, sigmoid, tanh等}之一。现在流行的激活函数就更加丰富了,请阅读:最近流行的激活函数。
接下来简单说说前向和反向传播的简单理解与计算
反向传播是利用链式法则递归计算表达式的梯度的方法。理解反向传播过程及其精妙之处,对于理解、实现、设计和调试神经网络非常关键。
问题陈述:这节的核心问题就是:给定函数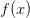
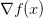
目标:之所以关注上述问题,是因为在神经网络中f(x)对应的是损失函数(L),输入x里面包含训练数据和神经网络的权重。
举个例子:
损失函数可以是SVM的损失函数,输入则包含了训练数据(xi,yi),i=1,...,N、权重W和偏差b。注意训练集是给定的,而权重是可以控制的变量。因此,即使能用反向传播计算输入数据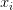
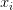
使用链式法则计算复合表达式
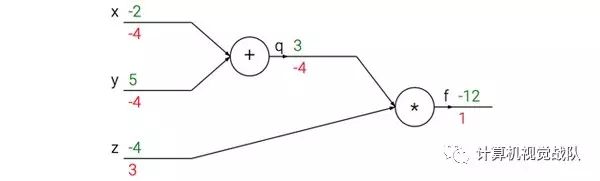
现在考虑更复杂的包含多个函数的复合函数,比如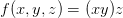
在前面已经介绍过如何对这分开的两个公式进行计算,因为f是q和z相乘,所以:
又因为q是x加y,所以:
然而,并不需要关心中间量q的梯度,因为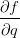
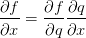
最后得到变量的梯度[dfdx, dfdy, dfdz],它们告诉我们函数f对于变量[x, y, z]的敏感程度。这是一个最简单的反向传播。一般会使用一个更简洁的表达符号,这样就不用写df了。这就是说,用dq来代替dfdq,且总是假设梯度是关于最终输出的。
这次计算可以被可视化为如下计算线路图像:
上图的真实值计算线路展示了计算的视觉化过程。前向传播从输入计算到输出(绿色),反向传播从尾部开始,根据链式法则递归地向前计算梯度(显示为红色),一直到网络的输入端。可以认为,梯度是从计算链路中回流。
真正开始讲解CNN
在图像处理中,往往把图像表示为像素的向量,比如一个1000×1000的图像,可以表示为一个1000000的向量。如果隐含层数目与输入层一样,即也是1000000时,那么输入层到隐含层的参数数据为1000000×1000000=10^12,这样就太多了,基本没法训练。所以图像处理要想练成神经网络大法,必先减少参数加快速度。
局部感知
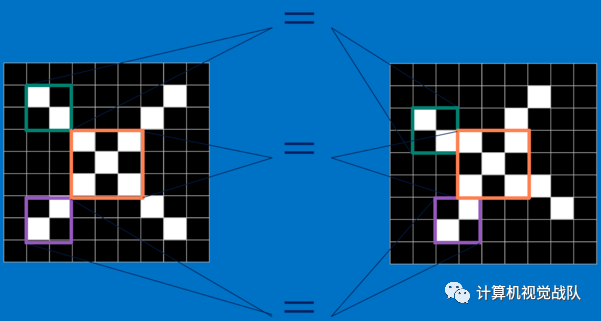
感受野可以理解为模仿人类视觉感知,人类看某个事物的时候,其实聚集点都是在局部小的局域。卷积神经网络有两种经典的方式可以降低参数数目,第一种方式叫做局部感知野。一般认为人对外界的认知是从局部到全局的,而图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。网络部分连通的思想,也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的(即这些神经元只响应某些特定区域的刺激)。如下图所示:上图为全连接,下图为局部连接。
参数共享
如果使用了局部感受野,其实这样的参数仍然过多,那么就用第二个经典方式,即权值共享。在上面的局部连接中,每个神经元都对应100个参数,一共1000000个神经元,如果这1000000个神经元的100个参数都是相等的,那么参数数目就变为100了。
可以把这100个参数看成是提取特征的方式,该方式与位置无关。这其中隐含的原理则是:图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征。
更直观一些,当从一个大尺寸图像中随机选取一小块,比如说 8×8 作为样本,并且从这个小块样本中学习到了一些特征,这时可把从这个 8×8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,可以用从 8×8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
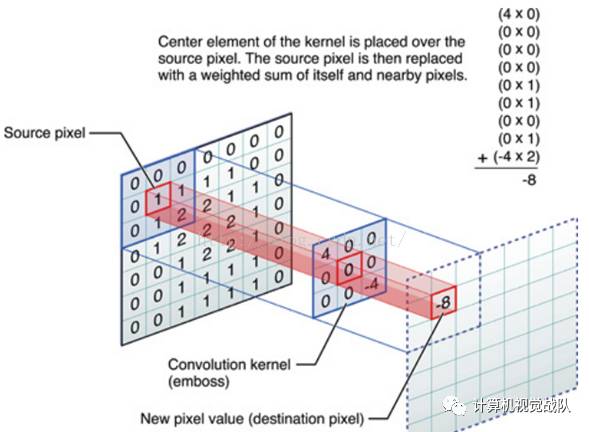
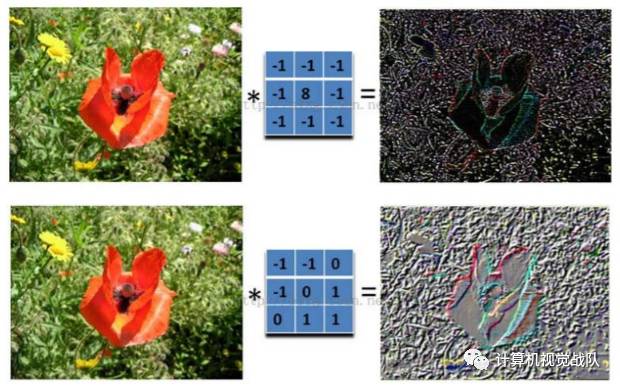
如下图所示,展示了卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。
图像上的卷积
在下图对应的计算过程中,输入是一定区域大小(width*height)的数据,和滤波器filter(带着一组固定权重的神经元)做内积后等到新的二维数据。
具体来说,左边是图像输入,中间部分就是滤波器filter(带着一组固定权重的神经元),不同的滤波器filter会得到不同的输出数据,比如颜色深浅、轮廓。相当于如果想提取图像的不同特征,则用不同的滤波器filter,提取想要的关于图像的特定信息:颜色深浅或轮廓。
下面简单说说激活函数
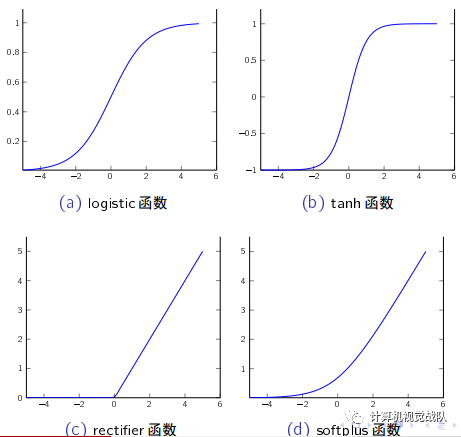
传统神经网络中最常用的激活函数分别是 sigmoid型函数。 sigmoid型函数
是指一类 S型曲线函数,常用的 sigmoid型函数有 logistic函数 和 tanh函数。
rectier函数 定义为
rectier(x) = max(0; x)
rectier函数被认为有生物上的解释性。神经科学家发现神经元具有单侧抑
制、宽兴奋边界、稀疏激活性等特性。采用 rectier函数的单元也叫作修正线性单元(rectied linear unit, ReLU)。
softplus函数 定义为:
softplus(x) = log(1 + ex )
softplus函数可以看作是 rectier函数的平滑版本,其导数刚好是 logistic函
数。 softplus虽然也有具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活
性。
子采样层
卷积层虽然可以显著减少连接的个数,但是每一个特征映射的神经元个数并没有显著减少。这样,如果后面接一个分类器,分类器的输入维数依然很高,很容易出现过拟合。为了解决这个问题,在卷积神经网络一般会在卷积层之后再加上一个池化(Pooling)操作,也就是子采样(Subsampling),构成一个子采样层。子采样层可以来大大降低特征的维数,避免过拟合。
对于卷积层得到的一个特征映射 X (l),我们可以将 X (l) 划分为很多区域
Rk; k = 1; ; K,这些区域可以重叠,也可以不重叠。一个子采样函数
down(····)定义为:
其中, w (l+1) 和 b(l+1) 分别是可训练的权重和偏置参数。
down(X l)是指子采样后的特征映射。
子采样函数 down()一般是取区域内所有神经元的最大值(Maximum
Pooling)或平均值(Average Pooling)。
子采样的作用还在于可以使得下一层的神经元对一些小的形态改变保持不
变性,并拥有更大的感受野。
案例
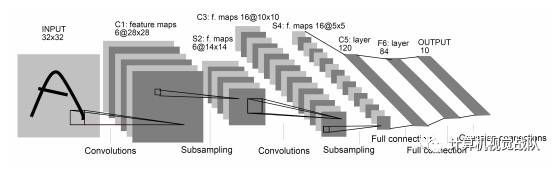
卷积神经网络示例: LeNet-5
LeNet-5虽然提出时间比较早,但是是一个非常成功的神经网络模型。基于 LeNet-5的手写数字识别系统在 90年代被美国很多银行使用,用来识别支票上面的手写数字。 LeNet-5的网络结构如下图所示。
不计输入层, LeNet-5共有 7层,每一层的结构为:
输入层:输入图像大小为 32X32 = 1024;
C1层:这一层是卷积层。滤波器的大小是 5 X5 = 25,共有 6个滤波
器。得到 6组大小为 28X28 = 784的特征映射。因此, C1层的神经元
个数为 6X784 = 4704。可训练参数个数为 6X25 + 6 = 156。连接数为 156X784 = 122304(包括偏置在内,下同)。S2层:这一层为子采样层。由 C1层每组特征映射中的 2X2 邻域点次采样为 1个点,也就是 4个数的平均。这一层的神经元个数为14X14 = 196。可训练参数个数为 6X(1 + 1) = 12。连接数为6X196X(4 + 1) = 122304 (包括偏置的连接)。
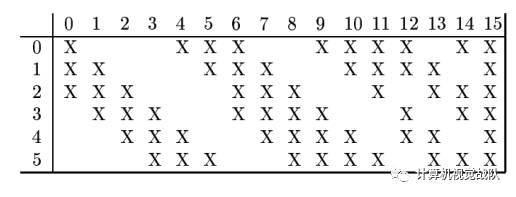
C3层:这一层是卷积层。由于 S2层也有多组特征映射,需要一个连接表来定义不同层特征映射之间的依赖关系。 LeNet-5的连接表如下图所示。这样的连接机制的基本假设是: C3层的最开始的 6个特征映射依赖于 S2层的特征映射的每 3个连续子集。接下来的 6个特征映射依赖于 S2层的特征映射的每 4个连续子集。再接下来的 3 个特征映射依赖于 S2层的特征映射的每 4个不连续子集。最后一个特征映射依赖于 S2层的所有特征映射。这样共有 60个滤波器,大小是5X5 = 25。得到 16组大小为 10X10 = 100的特征映射。C3层的神经元个数为 16X100 = 1600。可训练参数个数为(60X25 + 16 = 1516。连接数为 1516X100 = 151600。
S4层:这一层是一个子采样层,由 2X2邻域点次采样为 1个点,得到16组 5X5大小的特征映射。可训练参数个数为16X2 = 32。连接数为 16X(4 + 1) = 2000。
C5层:卷积层,得到120组大小为1X1的特征映射。每个特征映射与 S4层的全部特征映射相连。有120X16=1920 个滤波器,大小是5X5 = 25。C5层的神经元个数为120,可训练参数个数为1920X25+120 = 48120。连接数为 120X(16X25 + 1) = 48120。
F6层:是一个全连接层,有 84个神经元,可训练参数个数为84X(120 + 1) = 10164。连接数和可训练参数个数相同,为 10164。
输出层:输出层由 10个欧氏径向基函数(Radial Basis Function,RBF)函数组成。这里不再详述。
一下是简单的代码(若有兴趣可以阅读一番):
1、导入必要的模块
import cPickle
import gzip
import os
import sys
import time
import numpy
import theano
import theano.tensor as T
from theano.tensor.signal import downsample
from theano.tensor.nnet import conv
2、定义LeNetConvPoolLayer
class LeNetConvPoolLayer(object):
def __init__(self, rng, input, filter_shape, image_shape, poolsize=(2, 2)):
assert image_shape[1] == filter_shape[1]
self.input = input
#每个隐层神经元(即像素)与上一层的连接数为num input feature maps * filter height * filter width。
fan_in = numpy.prod(filter_shape[1:])
#lower layer上每个神经元获得的梯度来自于:"num output feature maps * filter height * filter width" /pooling size
fan_out = (filter_shape[0] * numpy.prod(filter_shape[2:]) /
numpy.prod(poolsize))
#以上求得fan_in、fan_out ,将它们代入公式,以此来随机初始化W,W就是线性卷积核
W_bound = numpy.sqrt(6. / (fan_in + fan_out))
self.W = theano.shared(
numpy.asarray(
rng.uniform(low=-W_bound, high=W_bound, size=filter_shape),
dtype=theano.config.floatX
),
borrow=True
)
#偏置b是一维向量,每个输出图的特征图都对应一个偏置,
#而输出的特征图的个数由filter个数决定,因此用filter_shape[0]即number of filters来初始化
b_values = numpy.zeros((filter_shape[0],), dtype=theano.config.floatX)
self.b = theano.shared(value=b_values, borrow=True)
#将输入图像与filter卷积,conv.conv2d函数
#卷积完没有加b再通过sigmoid,这里是一处简化。
conv_out = conv.conv2d(
input=input,
filters=self.W,
filter_shape=filter_shape,
image_shape=image_shape
)
#maxpooling,最大子采样过程
pooled_out = downsample.max_pool_2d(
input=conv_out,
ds=poolsize,
ignore_border=True
)
#加偏置,再通过tanh映射,得到卷积+子采样层的最终输出
#因为b是一维向量,这里用维度转换函数dimshuffle将其reshape。比如b是(10,),则b.dimshuffle('x', 0, 'x', 'x'))将其reshape为(1,10,1,1)
self.output = T.tanh(pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
#卷积+采样层的参数
self.params = [self.W, self.b]
3、定义隐含层HiddenLayer
class HiddenLayer(object):
def __init__(self, rng, input, n_in, n_out, W=None, b=None,
activation=T.tanh):
self.input = input
#类HiddenLayer的input即所传递进来的input
#如果W未初始化,则根据上述方法初始化。
#加入这个判断的原因是:有时候我们可以用训练好的参数来初始化W。
if W is None:
W_values = numpy.asarray(
rng.uniform(
low=-numpy.sqrt(6. / (n_in + n_out)),
high=numpy.sqrt(6. / (n_in + n_out)),
size=(n_in, n_out)
),
dtype=theano.config.floatX
)
if activation == theano.tensor.nnet.sigmoid:
W_values *= 4
W = theano.shared(value=W_values, name='W', borrow=True)
if b is None:
b_values = numpy.zeros((n_out,), dtype=theano.config.floatX)
b = theano.shared(value=b_values, name='b', borrow=True)
#用上面定义的W、b来初始化类HiddenLayer的W、b
self.W = W
self.b = b
#隐含层的输出
lin_output = T.dot(input, self.W) + self.b
self.output = (
lin_output if activation is None
else activation(lin_output)
)
#隐含层的参数
self.params = [self.W, self.b]
4、定义分类器
class LogisticRegression(object):
def __init__(self, input, n_in, n_out):
#W大小是n_in行n_out列,b为n_out维向量。即:每个输出对应W的一列以及b的一个元素。
self.W = theano.shared(
value=numpy.zeros(
(n_in, n_out),
dtype=theano.config.floatX
),
name='W',
borrow=True
)
self.b = theano.shared(
value=numpy.zeros(
(n_out,),
dtype=theano.config.floatX
),
name='b',
borrow=True
)
self.p_y_given_x = T.nnet.softmax(T.dot(input, self.W) + self.b)
self.y_pred = T.argmax(self.p_y_given_x, axis=1)
#params,LogisticRegression的参数
self.params = [self.W, self.b]
5、实现LeNet5并测试
def evaluate_lenet5(learning_rate=0.1, n_epochs=200,
dataset='mnist.pkl.gz',
nkerns=[20, 50], batch_size=500):
rng = numpy.random.RandomState(23455)
#加载数据
datasets = load_data(dataset)
train_set_x, train_set_y = datasets[0]
valid_set_x, valid_set_y = datasets[1]
test_set_x, test_set_y = datasets[2]
# 计算batch的个数
n_train_batches = train_set_x.get_value(borrow=True).shape[0]
n_valid_batches = valid_set_x.get_value(borrow=True).shape[0]
n_test_batches = test_set_x.get_value(borrow=True).shape[0]
n_train_batches /= batch_size
n_valid_batches /= batch_size
n_test_batches /= batch_size
#定义几个变量,index表示batch下标,x表示输入的训练数据,y对应其标签
index = T.lscalar()
x = T.matrix('x')
y = T.ivector('y')
print '... building the model'
layer0_input = x.reshape((batch_size, 1, 28, 28))
layer0 = LeNetConvPoolLayer(
rng,
input=layer0_input,
image_shape=(batch_size, 1, 28, 28),
filter_shape=(nkerns[0], 1, 5, 5),
poolsize=(2, 2)
)
layer1 = LeNetConvPoolLayer(
rng,
input=layer0.output,
image_shape=(batch_size, nkerns[0], 12, 12),
#输入nkerns[0]张特征图,即layer0输出nkerns[0]张特征图
filter_shape=(nkerns[1], nkerns[0], 5, 5),
poolsize=(2, 2)
)
layer2_input = layer1.output.flatten(2)
layer2 = HiddenLayer(
rng,
input=layer2_input,
n_in=nkerns[1] * 4 * 4,
n_out=500,
activation=T.tanh
)
layer3 = LogisticRegression(input=layer2.output, n_in=500, n_out=10)
#代价函数NLL
cost = layer3.negative_log_likelihood(y)
#test_model的输入是x、y,输出是layer3.errors(y)的输出,即误差。
test_model = theano.function(
[index],
layer3.errors(y),
givens={
x: test_set_x[index * batch_size: (index + 1) * batch_size],
y: test_set_y[index * batch_size: (index + 1) * batch_size]
}
)
#validate_model,验证模型,分析同上。
validate_model = theano.function(
[index],
layer3.errors(y),
givens={
x: valid_set_x[index * batch_size: (index + 1) * batch_size],
y: valid_set_y[index * batch_size: (index + 1) * batch_size]
}
)
params = layer3.params + layer2.params + layer1.params + layer0.params
#对各个参数的梯度
grads = T.grad(cost, params)
updates = [
(param_i, param_i - learning_rate * grad_i)
for param_i, grad_i in zip(params, grads)
]
#train_model,代码分析同test_model。train_model里比test_model、validation_model多出updates规则
train_model = theano.function(
[index],
cost,
updates=updates,
givens={
x: train_set_x[index * batch_size: (index + 1) * batch_size],
y: train_set_y[index * batch_size: (index + 1) * batch_size]
}
)
###############
# 开始训练 #
###############
print '... training'
patience = 10000
patience_increase = 2
improvement_threshold = 0.995
validation_frequency = min(n_train_batches, patience / 2)
#这样设置validation_frequency可以保证每一次epoch都会在验证集上测试。
best_validation_loss = numpy.inf
#最好的验证集上的loss,最好即最小
best_iter = 0
#最好的迭代次数,以batch为单位。比如best_iter=10000,说明在训练完第10000个batch时,达到best_validation_loss
test_score = 0.
start_time = time.clock()
epoch = 0
done_looping = False
while (epoch < n_epochs) and (not done_looping):
epoch = epoch + 1
for minibatch_index in xrange(n_train_batches):
iter = (epoch - 1) * n_train_batches + minibatch_index
if iter % 100 == 0:
print 'training @ iter = ', iter
cost_ij = train_model(minibatch_index)
if (iter + 1) % validation_frequency == 0:
validation_losses = [validate_model(i) for i
in xrange(n_valid_batches)]
this_validation_loss = numpy.mean(validation_losses)
print('epoch %i, minibatch %i/%i, validation error %f %%' %
(epoch, minibatch_index + 1, n_train_batches,
this_validation_loss * 100.))
if this_validation_loss < best_validation_loss:
if this_validation_loss < best_validation_loss * \
improvement_threshold:
patience = max(patience, iter * patience_increase)
best_validation_loss = this_validation_loss
best_iter = iter
test_losses = [
test_model(i)
for i in xrange(n_test_batches)
]
test_score = numpy.mean(test_losses)
print((' epoch %i, minibatch %i/%i, test error of '
'best model %f %%') %
(epoch, minibatch_index + 1, n_train_batches,
test_score * 100.))
if patience <= iter:
done_looping = True
break
end_time = time.clock()
print('Optimization complete.')
print('Best validation score of %f %% obtained at iteration %i, '
'with test performance %f %%' %
(best_validation_loss * 100., best_iter + 1, test_score * 100.))
print >> sys.stderr, ('The code for file ' +
os.path.split(__file__)[1] +
' ran for %.2fm' % ((end_time - start_time) / 60.))