SOS—操弄对称的相似原理 (下)
海归学者发起的公益学术平台
分享信息,整合资源
交流学术,偶尔风月
无 题
编者按
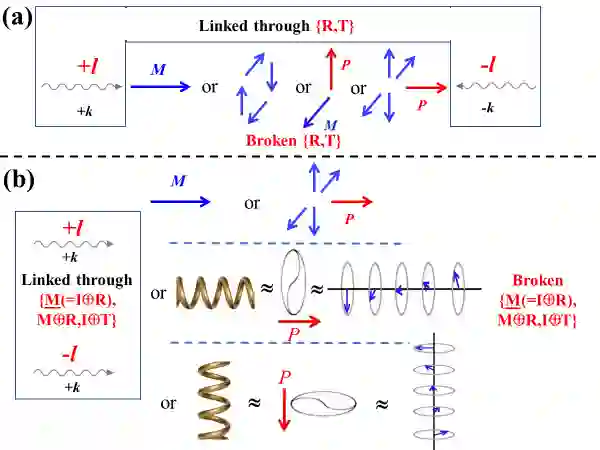
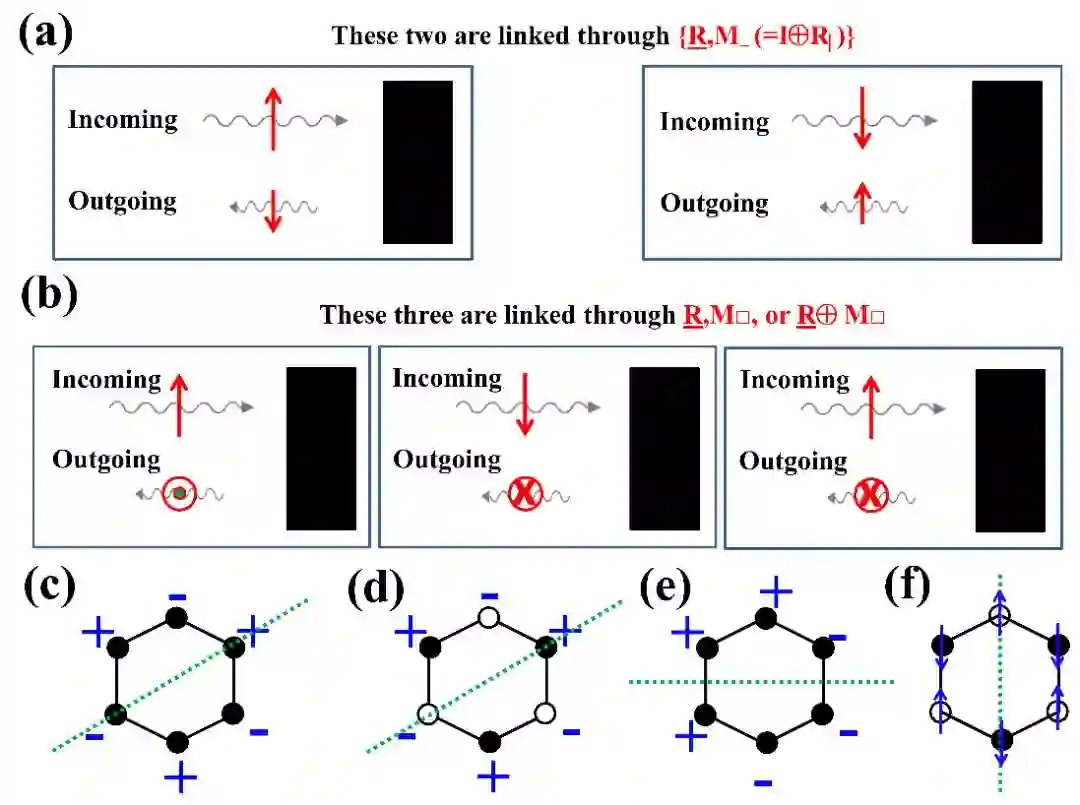
角动量与非互易
SOS之拓展:准静态电子输运
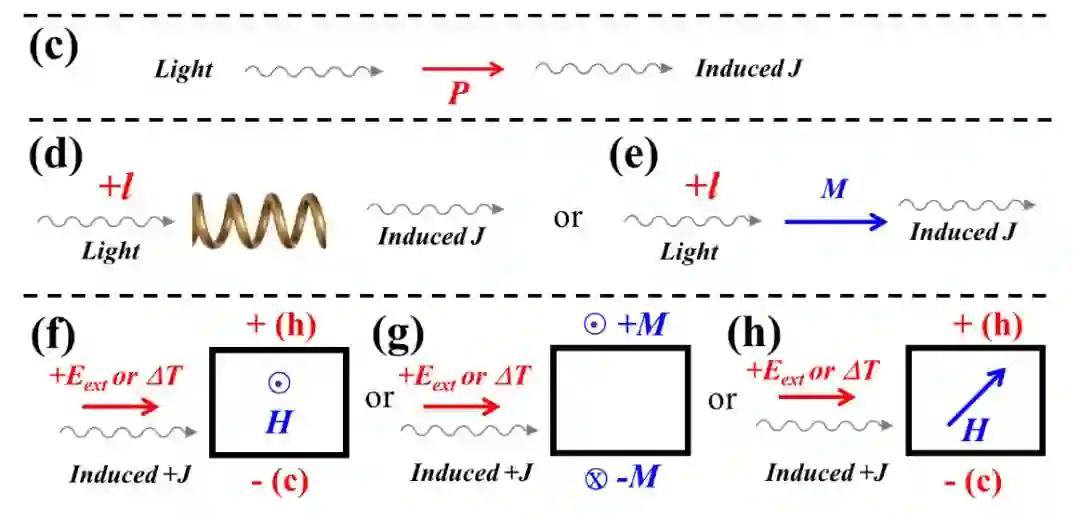
MOKE 型旋光
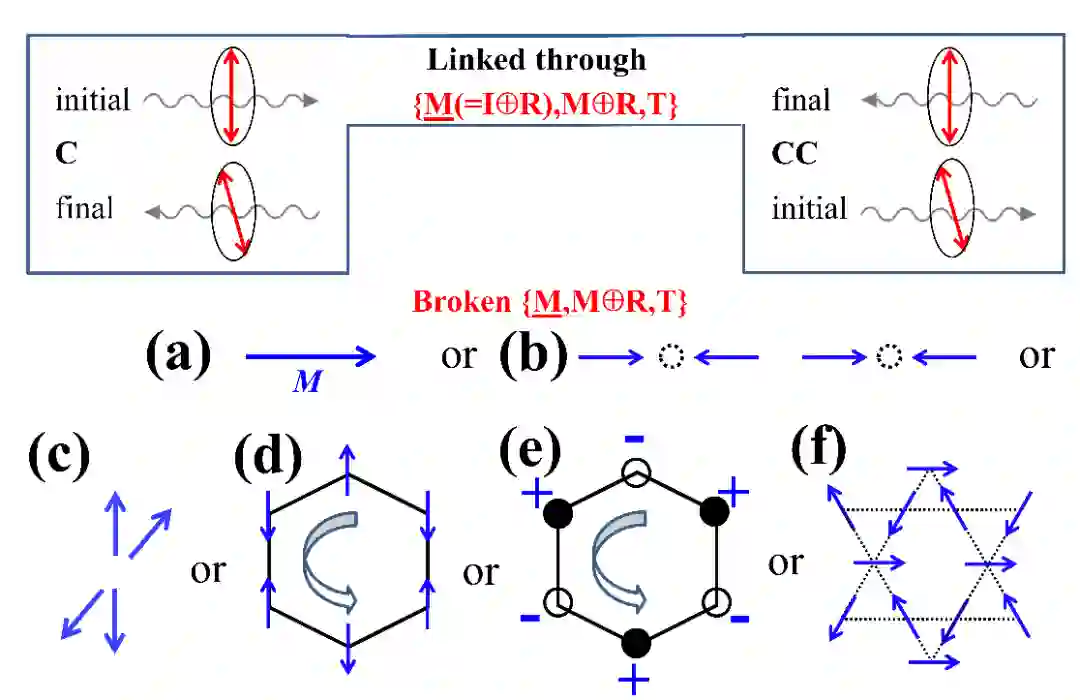
二次谐波发生 (SHG)
总结与展望
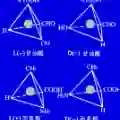
磁螺旋序具备关于结构手性的 SOS,将能展现出旋光性;
在图 2(c) 单轴手性材料中,将能出现光学传输或电子输运的横向磁 - 手性效应;
对图 2(g) 中由旋转自旋构成的环磁极矩,能够观察到非偏振光或自旋波传播的非互易性;
当Neel 型铁电畴壁沿着垂直于畴壁的方向运动时,能够诱导出垂直于极化旋转方向的磁性;
图 5 以及图 6(a) & 6(b) 中很多未在实际材料中观察到或考虑过的现象;
图 6(c) 中未在实际材料中观察到或考虑过的铁磁/亚铁磁 CPGE 效应;
图 6(f) 中未在实际材料中观察到或考虑过的非线性霍尔型输运性质。这些性质从技术来看,应该比较容易在实验中得到检验;
图 7 中磁单极子系统和具有反铁磁伊辛序的 (翘曲) 蜂窝系统中,可能存在 MOKE 型旋光性;
利用 SHG 成像技术观察图 8(c) & 8(e) & 8(f) 中的反铁磁 (翘曲) 蜂窝晶格系统。
后话
最后,略显遗憾的是,SOS 原理既不能说明物理现象的微观机制,也不能预估它们的大小。不过,正如在图 4(a)中所展示的那样,所有具有螺旋自旋序的磁体在实验中均展现了可观测的极化 P。我们坚信,如果某一物理现象在对称性破缺考虑下是允许的,那么这个效应通常就足够大到可以被实验所观测。这似乎与著名的 Murray Gell-Mann 论述遥相呼应:“everything not forbidden is compulsory (只要没有基本原理禁止它发生,它就可以发生)” [61]。
[39] Allen, L., Beijersbergen, M. W., Spreeuw, R. J. C. & Woerdman, J. P. Orbital angular-momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 45, 8185-8189 (1992).
[40] Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. Nat. Phys. 3, 305 (2007).
[41] Yuan, J., Lloyd, S. M., & Babiker, M. Mechanical properties of electron vortices. Phys. Rev. A 88, 031801(R) (2013).
[42] Verbeeck, J., Tian, H. & Schattschneider, P. Production and application of electron vortex beams. Nature 467, 301-304 (2010).
[43] Sirenko A. A. et al. Terahertz vortex beam as aspectroscopic probe of magnetic excitations. Phys. Rev. Lett. 122, 237401 (2019).
[44] Buckingham A. D. & Stephens P. J. Magnetic optical activity. Annu. Rev. Phys. Chem. 17, 399-432 (1966).
[45] Vlokh, O. G., Zheludev, I. S. & Klimov, I. M. Electric field-induced optical activity of centrosymmetrical crystals of lead molybdate PbMoO4. Doklady Akademii Nauk SSSR. 223, 1391–1393(1975).
[46] Ivchenko, E. L. and Pikus, G. E. New photo galvanic effect in gyrotropic crystals. Pis’ma Zh. Eksp. Teor. Fiz. 27, 640 (1978); JETP Lett. 27, 604-608 (1978).
[47] Belinicher, V. I. Space-oscillating photo current in crystals without symmetry center. Phys. Lett. A 66, 213-214 (1978).
[48] Asnin, V. M., Bakun, A. A., Danishevskii, A. M., Ivchenko, E. L., Pikus, G. E., Rogachev, A. A. Observation of a photo-emf that depend on the sign of the circular polarization of the light. Pis’ma Zh.Eksp. Teor. Fiz. 28, 80-84 (1978); JETP Lett. 28, 74-77 (1978).
[49] Hall E. On a New Action of the Magnet on Electric Currents. Am. J. Math. 2, 287–92 (1879).
[50] v. Ettingshausen A. and Nernst W. Ueber das Auftreten electromotorischer Kräfte in Metallplatten, welche von einem Wärmestrome durchflossen werden und sich im magnetischen Felde befinden. Annalen der Physik und Chemie 265, 343–347 (1886).
[51] Dyakonov M. I. and Perel V. I. Possibility of orientating electron spins with current. JETP Lett. 13, 467-469 (1971).
[52] Kim D. J. et al. Observation of transverse spin Nernst magnetoresistance induced by thermal spin current in ferromagnet/non-magnet bilayers, Nature Commun. 8, 1400 (2017).
[53] Goennenwein S. T. B. et al. Planar Hall effect and magnetic anisotropy in epitaxially strained chromium dioxide thin films. Appl. Phys. Lett. 90, 142509 (2007).
[54] Wesenberg, D. Hojem, A. Bennet R. K. and Zink B. L. Relation of planar Hall and planar Nernst effects in thin film permalloy. J. Phys. D: Appl. Phys. 51, 244005 (2018).
[55] Nandy S., Taraphder A., and Tewari S. Planar thermal Hall effect in Weyl semimetals. arXiv: 1711.03102.
[56] Krichevtsov, B. B., Pavlov, V. V., Pisarev, R. V. & Gridnev, V. N. Spontaneous non-reciprocal reflection of light from antiferromagnetic Cr2O3. J. Phys. Condens. Matter 5, 8233-8244 (1993).
[57] Muthukumar, V. N., Valentí, R. & Gros, C. Theory of nonreciprocal optical effects in antiferromagnets: The case of Cr2O3. Phys. Rev. B 54, 433-440 (1996).
[58] Higo T. et al. Large magneto-optical Kerr effect and imaging of magnetic octupole domains in an antiferromagnetic metal. Nat. Photonics 12, 73-78 (2018).
[59] Fiebig, M., Frӧhlich, D. & Sluyterman G. & Pisarev R. V. Domain topography of antiferromagnetic Cr2O3 by second-harmonic generation. Appl. Phys. Lett. 66, 2906-2908 (1995).
[60] Yokosuk, M. O. et al. High-energy nonreciprocal directional dichroism in a chiral magnet. To be published.
[61] Gell-Mann, M. The interpretation of the new particles as displaced charge multiplets. Il NuovoCimento 4, 848-866 (1956).
备注:
(1) 题头小诗以示春华秋实之物理,乃对称最被钟情。这是物理的魅力和景色。
(2) 封面图片来自https://www.ics.usi.ch/index.php/group-bronstein/13-ics/projects/。
(3) 本文翻译得到作者授权并经Nature 出版集团同意。
点击左下角“阅读原文”查看论文原文。
扩展阅读
本文系网易新闻·网易号“各有态度”特色内容
媒体转载联系授权请看下方