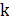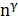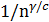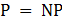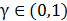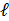预告 | 火爆！NIPS 2017注册已满，没机会去前方参会怎么办？

2017 年 9 月 21 日 AI科技评论 沐沐

人工智能关注度继续升温。

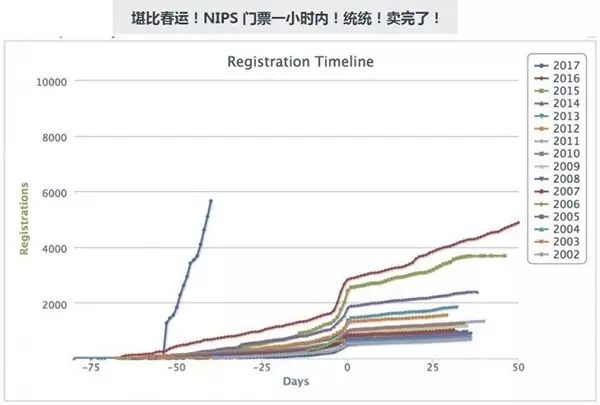
继CVPR 2017会议在报名人数以及论文收录等方面创下多项“历史第一”之后，计算神经科学最好的会议之一——NIPS（神经信息处理系统大会）在文章收录结果仅仅公布10天之后，官方数据显示注册名额已满！

（图片来源雷锋网）

NIPS是由连接学派（connectionist）神经网络的学者于1987年在加拿大创办，后来随着影响力逐步扩大，也曾移师美洲、欧洲等地举办。早年发布在NIPS中的论文包罗万象，从单纯的工程问题到使用计算机模型来理解生物神经元系统等各种主题。但现在论文的主题主要以机器学习，人工智能和统计学为主。在各种学术会议统计中，NIPS被认为有着很强的影响力和很高的排名。

今年的NIPS将于12月4日-9日在美国西岸加州南部城市长滩市（Long Beach）举办。在距离正式开会还有将近3个月的时候，注册人数已满足以看出本次会议的火爆程度。那么对于广大还没来得及注册或者没有机会去到前方的同学们来说，如何才能更进一步的了解本次NIPS的论文情况呢？

机会来了！第四期的“GAIR大讲堂”我们将再次回到北京清华，本次活动主办方雷锋网第一时间邀请到了NIPS 2017入选论文作者去到清华大学预讲入选论文同时分享他们投递论文的心得，相信他们的分享能够对广大同学们如何发Paper 起到重要帮助！

嘉宾介绍

陆洲北京大学数学科学学院大四本科生

陆洲，北京大学数学科学学院大四本科生，导师为王立威。NIPS 2017 一作论文一篇。主要关注机器学习理论，目前研究方向主要为神经网络的表达能力和泛化能力。

主题：从宽度来看神经网络的表达能力（The expressive power of neural networks : A view from the width）

分享内容：

深度学习应用火爆，难以掩盖其理论的缺少。神经网络对函数的表达能力，便是其理论重要的一部分。本文中，我们从宽度入手，得到了以下关于神经网络表达能力的新结果：

1、经典的一致逼近定理说明深度为2，不限制宽度，并使用适当激活函数的神经网络对任意紧集上连续函数能做到任意精度的一致逼近。这里我们得到了一个近似对偶的结论，设网络输入维数为n，则宽度为n+4，不限制深度的全连接relu网络对任意勒贝格可积函数能做到任意精度的积分意义逼近。

2、我们接着证明了宽度不足n的网络，其表达能力极差，勒贝格可积函数以概率为1无法被其逼近，由此得到了一个关于宽度的相变。

3、我们证明了存在一些深度为3的浅网络，需要深网络多项式级更多的节点才能逼近，并用实验说明，将这些深网络宽度扩大常数倍，就能极高精度逼近浅网络。

邓志杰清华大学计算机系人智所博士生

邓志杰，清华大学计算机系智能媒体实验室一年级博士生，导师为朱军。主要关注深度产生式模型，分布式机器学习等方向，现在主要研究生成对抗网络的理论和应用。

主题：结构化生成对抗网络（Structured Generative Adversarial Networks）

分享内容：

本工作研究基于指定语义或结构信息的条件产生式建模。现有的模型在搭建条件生成器时，往往需要大量的标注数据作为监督信号，而且不能够准确地对生成样本的语义信息加以控制。因此我们提出结构化生成对抗网络(SGAN) 来解决半监督条件产生式建模这个问题。SGAN 假设数据 x 基于两个独立的隐变量 y 和 z 来生成: y 编码了指定的语义信息，z 包含其他的可变因素。SGAN 的训练要解决两个对抗游戏，它们能够保证模型中各部分收敛到数据的真实联合分布p(x, y)和p(x, z)。为了确保 y 和 z 的解耦和，SGAN 搭建了两个合作游戏，它们在隐空间上最小化重建误差。我们进行了大量的实验来评估结构化生成对抗网络。我们的实验表明 SGAN 能够学习出一个高度可控的条件生成器，以及数据的解耦和的表示。SGAN 在半监督分类任务的多个数据集上都取得了很好的实验结果。得益于对 y 和 z 的分开建模，SGAN 能够生成高质量并且严格遵循指定语义的样本。此外，SGAN 还能被扩展来进行一些有趣的实验，包括图像演化和图像风格迁移。

陈键飞清华大学计算机系人智所博士生

陈键飞是清华大学计算机系博士四年级学生，导师为朱军副教授。主要从事大规模机器学习、产生式模型、话题模型的研究。在NIPS、VLDB、ICML等重要国际会议和NSR、TVCG等国际重要期刊发表学术论文10篇，其中第一作者/学生第一作者4篇。他曾获2009年全国青少年信息学奥林匹克竞赛（NOI）金牌。

主题：样本匹配差异及其在深度学习中的应用（Population Matching Discrepancy and Applications in Deep Learning）

分享内容：

两个概率分布之间可导的距离估计是对很多深度学习任务重要的问题。其中一种距离估计是最大平均差异（MMD）。但是MMD有对核半径敏感、梯度弱以及用于训练目标时mini batch过大等问题。

本次分享将围绕这一问题，介绍我们NIPS2017上提出的样本匹配差异（PMD）。我们提出了PMD作为分布之间距离的估计，并提出了用PMD作为目标函数时学习分布参数的算法。PMD定义成两分布样本构成的二分图的最小匹配，我们证明了PMD是Wasserstein度量的强一致估计量。我们把PMD用于了两个深度学习问题，包括领域自适应和训练产生式模型。实验结果表明PMD克服了上述MMD的不足，并在效果和收敛速度上都超过了MMD。

汪跃北京交通大学理学院博士生

汪跃，北京交通大学理学院在读博士生，专业是概率论与数理统计。2015年汪跃在北京交通大学信息与计算科学专业本科毕业，随后师从马志明院士，刘玉婷教授读博士，2016年加入微软亚洲研究院机器学习组(Machine Learning Group)做实习生。

虽然是数学专业，但是汪跃特别喜欢跟应用结合的相关领域。曾经做过一段时间与脑科学有关的影像遗传学方面的工作。最近感兴趣的方向主要集中在强化学习中的算法理论分析和算法设计等方面，以及优化算法相关的方向。

主题：马尔科夫情形下的GTD 策略评估算法有限样本误差分析（Finite sample analysis of the GTD Policy Evaluation Algorithms in Markov Setting）

分享内容：

策略评估是强化学习中一个重要的组成部分。策略评估的目标是估计给定策略的价值函数（从任一状态出发，依照给定的策略时，期望意义下未来的累计回报）。一个好的策略评估算法可以更准确的估计出当前策略的价值函数，并且有助于找到一个更好的策略。当状态空间特别大或者是连续空间的时候，线性函数近似下的GTD策略评估算法非常常用。考虑到收集数据的过程非常耗费时间和代价，清楚的理解GTD算法在有限样本情况下的表现就显得非常重要。之前的工作将GTD算法与鞍点问题建立了联系，并且在样本独立同分布和步长为定值的情况下给出了GTD算法的有限样本误差分析。但是，我们都知道，在实际的强化学习问题中，数据都是由马氏决策过程产生的，并不是独立同分布的。并且在实际中，步长往往也不一定是一个定值。

因此在我们的工作中，我们首先证明了在数据来自于马尔科夫链的情况下，鞍点问题的期望意义下和高概率意义下的有限样本误差，进而得到了更接近于实际情形下的GTD的算法的有限样本误差分析。从我们的结果中可以看到，在实际中的马尔科夫的情形下，（1）GTD算法确实依然收敛；（2）收敛的速率依赖于步长的设定和马尔科夫链的混合时间这一属性；（3）通过混合时间的角度解释了经验回放这一技巧的有效性，其有效性可以理解成缩短了马尔科夫链的混合时间。就我们所知，我们的工作首次给出了GTD算法在马尔科夫情形下的有限样本误差分析。

单小涵中国科学院计算技术研究所博士生

单小涵是中国科学院计算技术研究所的一名在读博士生，师从孙晓明研究员。她的研究兴趣包括社交网络，算法博弈论，组合最优化等。于2014和2011年在中国海洋大学分别获得硕士和学士学位。

主题：带有ε-近似次模阈值函数的影响力最大化问题（Influence Maximization with epsilon-Almost Submodular Threshold Function ）

分享内容：

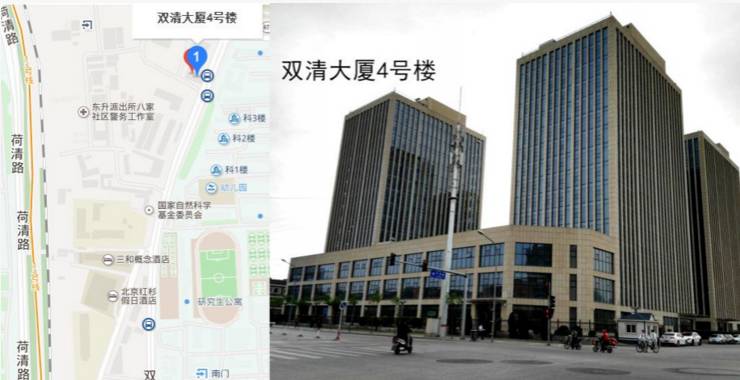
影响力最大化旨在从社交网络中选择个种子节点，使得这个种子节点通过传播产生的影响范围最大。这个问题已经被广泛研究，但是大多的工作专注于次模的影响力传播模型。然而许多现实的传播现象表明，在实际传播中非次模现象十分普遍。在此背景下，我们提出了一类具有次模上下界的-近似次模函数，并以这类函数作为阈值，研究通用阈值模型下的影响力最大化问题。我们首先证明了不可近似性结论：如果一个n个节点的图中有个非次模阈值节点，那么就不存在近似比为的算法，除非，其中且是依赖于的常数。然后我们针对有个-近似次模阈值函数节点的图设计了近似比为的算法。最后我们在一系列真实的社交网络数据上做了对比试验，实验结果表明我们提出的近似算法比其他基准算法效果更好。