双人协作游戏带你理解变分自编码器-Part2

2018 年 5 月 3 日 专知

【导读】本文是AI研究员Max Frenzel关于变分自编码器的系列教程的Part 2。在part 1的教程中，作者从双人协作游戏的角度介绍了自编码器的原理，本文介绍了为解决自编码器的缺点而提出的变分自编码器。同样是使用双人协作游戏来举例，使用重新参数化的技巧来使解码器能提供给编码器有用的反馈信息。具体内容参见本文详情。

双人协作游戏带你理解变分自编码器-Part1

编译 | 专知

参与 | Yingying, Xiaowen

欢迎来到关于变分自动编码器系列的part 2，以及它们在编码文本中的应用。

在part 1中，我们跟随我们的两位选手Alice和Bob，因为他们正在训练自动编码奥运会。我们学习了自动编码器的基础知识、一般的深度学习算法，以及Alice和Bob可能学习的代码类型。我们也看到，传统的自动编码器有单纯记忆内而不是进行学习的风险。这最终导致了Alice和Bob在奥运会上的失败表现，因为他们遇到了以前从未见过的数据。

引入变分自动编码器(VAE)【1】

回到家后，他们对自己在自动编码奥运会上的糟糕表现感到非常沮丧，Alice和Bob重新组合，并考虑如何改变他们的下一场比赛的方式。因为他们的经历是失败的，他们没有得到一个哪怕是正确的测试图像，他们决定从头开始。所以Alice和Bob把他们想出来的编码扔掉，进行一场史诗式的狂欢，把他们所学到的一切都从他们的脑海中抹去。

他们的头脑又完全空白了。就像我们第一次见到他们一样。他们决定将自己的自动编码器升级到他们最近听说的一个新的方法——变分模型。变分模型只建议专家级编码器/解码器来使用。它只是用来训练的，这实际上使过程更加困难。但是Alice和Bob想通过它要成为游戏的高手。

没有痛苦就没有收获。最初的模型实际上只是一组代码和反馈的发送者和接收者。新方法略有不同。让我们看看它们是如何工作的。

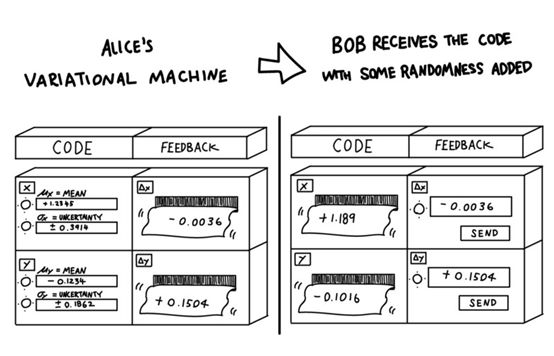
Alice仍然输入她认为最有可能的编码。但除此之外，她也要进入一个不确定的状态！基于此，机器不会直接将Alice输入的值传递给Bob。相反，它根据输入的分布选择一个随机数。它随机抽取了Alice的编码分布。因此，Bob仍然只得到每个编码维度的单个数字。但是这个数字在从Alice的机器转移到Bob的过程中获得了一点随机性。

实际上，引入VAE的原始论文的主要贡献之一是使用：重新参数化技巧（reparametrization trick），它允许Bob在不知道Alice所选择的精确值的情况下，给Alice提供有用的反馈，但只有机器传递给他的随机变量。

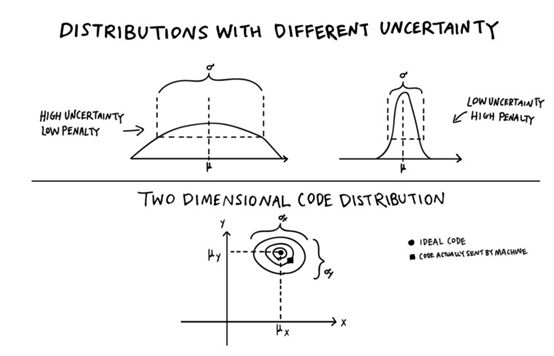
原则上，Alice仍然可以选择输入非常低的不确定性，这样Bob几乎可以得到她想要传输的准确值。但问题是Charlie变得更严格了。他现在也从他们的得分中减去了一个惩罚。Alice所选择的不确定性越小，Charlie的惩罚就越大。如果Alice有信心，哪怕只是接近她想要的值，仍然可以传递所有的信息，她可以选择更高的不确定性和损失更少的分数。另一方面，如果编码需要非常精确地将图像传送给Bob，那么Alice需要选择一个低的不确定性。这样，即使Bob完美地重构了图像并为他们赢得了一个完美的分数，他们也因为不确定性的惩罚而失去了很多。

这迫使Alice和Bob更聪明地选择他们所用的编码。它需要更有力地应对小变化。即使代码在传输过程中被扭曲了一点，Bob还是应该画一幅相当相似的画。

消除编码

让我们再来看看用一个数字编码的极端例子。

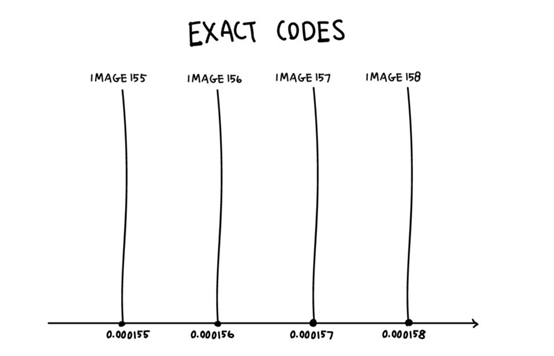
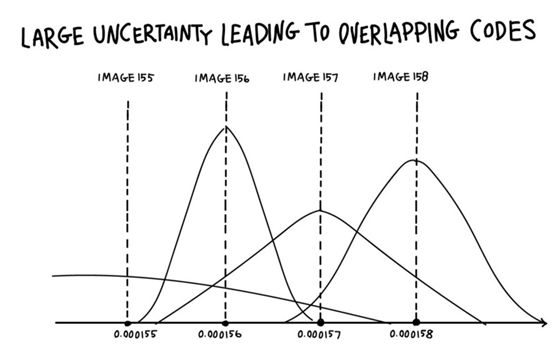
我们在Part 1中看到，没有不确定性，Alice和Bob可以学习如何将一个唯一的代码编号与他们的每个训练图像关联起来，基本上记住了他们的整个训练数据集。在一个特定的代码中，Alice可以将连续编号的图像编码为0.000001。图像156对应代码0.000156，图像157到0.000157，等等。而不管这些图像实际上包含什么。如果Bob得到了准确的数字，他已经通过多次反复的尝试和错误学习了相应的图像。

问题是，这会在代码中创建“漏洞”。Alice从来没有在空间中编码任何东西，例如0.000156和0.000157。因此，这些间隙中的任何数字，比如0.0001561或0.0001568，对Bob来说都是毫无意义的。当然，他可以把他和一个图像联系在一起，或者向下移动到最近的数字，但是这意味着他们的代码在像0.0001565这样的地方有一个急剧的转变。代码中最小的变化可能意味着Bob必须绘制完全不同的图像。它也不能用于对不熟悉的图像进行编码而无需进一步的训练和修改。这导致了他们在part1的失败。

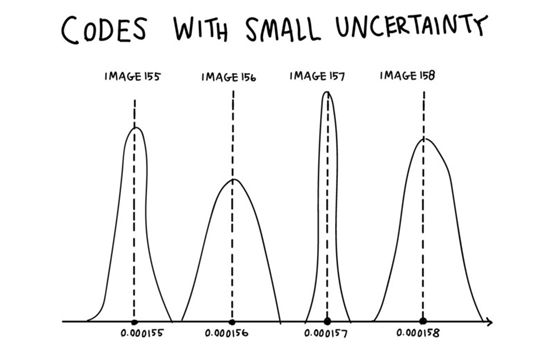
然而，当Alice开始使用少量的不确定性时，她开始“填充漏洞”，并稍微平滑了他们的编码。

如果她想发送图像156，并输入0.000156的小的不确定性，Bob将得到一个接近它的数字，但可能不完全相同。当他们多次使用相同的图像进行相同的游戏时，即使Alice的代码没有改变，Bob仍然会看到几个与每个图像相关的稍微不同的数字。这已经帮助他们减少了对精确数字的依赖。

但是这样微小的不确定性仍然会带来很高的惩罚！

如果他们真的想要获得成功，并从Charlie那里获得一个好的整体分数，他们需要弄清楚如何想出一个能使不确定性高得多的编码。如果Alice仍然想要将图像编码为0.000156，图像为0.000157，那么她最好确保这两个图像几乎是相同的，除非他们想通过牺牲大量的分数来选择微小的不确定性。

因此，除非这两张图片非常相似，否则这段编码是非常浪费的，应该避免。

如果不确定度小于0.000001，那么即使Alice想要编码图像157，也有很大的可能性这台机器实际上会发送她选择的代码，以图像156给Bob，或者更不一样的东西。然后，即使Bob理解了Alice的代码，他仍然会画出错误的图像。如果他们想要获得高分，同时保持低的惩罚，他们必须学会用类似的代码来编码相似的图像。

获得有意义的代码

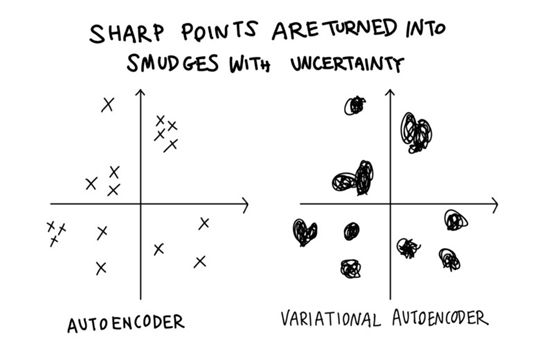
回到完整的游戏和一个二维的代码，我们也可以用稍微不同的方式来思考这个问题。而不是将每个图像编码成二维平面上的一个点，Alice现在必须将它们编码成小的smudges（污点）。smudges越小，惩罚越高。

你可以把无穷多的点塞入一个极小的空间。另一方面的污点很快就会开始重叠，所以你最好确保重叠的部分是有意义的。

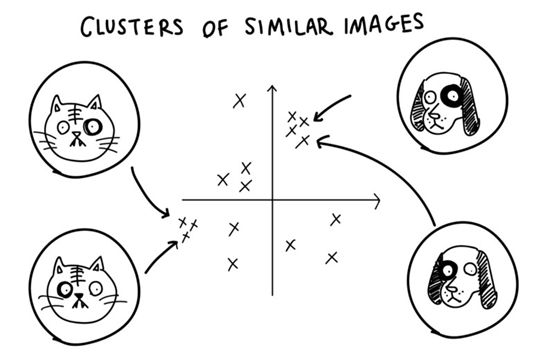
使用这台新机器和Charlie的更严格的计分策略使他们无法记住训练数据。他们需要给他们的代码赋予实际意义。这迫使他们提出一种平滑的、连续的代码，因此“代码空间”(也称为“潜在空间”)中的相邻区域在“数据空间”中编码非常相似的图像。这样他们就不会牺牲太多的分数，因为他们必须非常准确地指出这个点，而且是不确定的。这自然会导致代码空间的集群化。

他们学到的改进后的代码更有意义。与直接编码图像相比，代码实际上包含了更多的抽象概念，就像我们在part 1中讨论的那样。在一个区域，我们可能会在照片的右下角看到白色吉娃娃的图片，在另一个区域，所有的图片都是黑猫在照片的中心玩球，等等。所有的转换都尽可能的平稳，这样相邻的图像就尽可能的相似。

离开Alice和Bob的世界一会儿，Laurens van der Maaten和Geoffrey Hinton为著名的MNIST数据集制作了一个很好的可视化的聚类(参考链接【2】），包括许多不同的数字0到9的图像。

我们看到类似的数字聚在一起，比如左下角的零。但是，在每个数字集群中，我们看到相似的样式(例如，倾斜，笔画宽度，…)聚集在一起。

回头来看Alice和Bob。随着他们从变分训练中获得的新经验，他们回到了下一个自动编码的奥运会。在这里，他们简单地回到原来的策略，在那里Alice直接传递代码而不使用任何不确定性。

但至关重要的是，他们使用了通过变分训练学习的新编码。训练也得到了回报!

有了这段代码，他们就能在训练中取得成功并彻底摧毁他们的竞争对手。

游戏时间

为了庆祝他们的胜利，他们用他们的学习代码来玩。他们发现了一些现在可以表演的有趣的戏法。第一个允许他们平滑地插入真实的照片。然后，它们可以编码两个真实的图像，为每个图像获取一个代码，然后通过使用中间代码和让Bob对它们进行解码，从而顺利地从一个到另一个。

一个简单的例子，让我们假设他们用人的图像重复他们的训练，然后对他们自己的照片进行编码，其中一个是Alice，另一个是Bob。举个例子，假设Alice的代码是(0.0,3.0)，Bob的是(6.0,0.0)。他们现在可以在他们之间不断地转换。

假设他们解码了两个等距的中间图像。这些中间图像应该是(2.0,2.0)和(4.0,1.0)。当Bob解码时，他们看到(2.0,2.0)的照片基本上是66.6% Alice和33.3% Bob，而一个 (4.0, 1.0)的比例是相反的，33.3% Alice和66.6% Bob。

但至关重要的是，这不仅仅是你可以在Photoshop中轻松完成的原始照片。这真的是看起来像“三分之一Alice和三分之二Bob”。

这样，VAEs允许创建绝对真实的、不存在于现实世界中的数据。例如，我们可以对自己和伴侣的照片进行编码，并在他们之间插值来猜测我们的孩子可能是什么样子(假设他们也变成了某种性别混合的人)。

对于一个真实的照片插值的例子，可以看看这段非常有趣的关于名人脸插值的视频。

视频地址：https://www.youtube.com/watch?v=36lE9tV9vm0

这不仅仅局限于图像。我们将在下一部分中看到，我们也可以对其他类型的数据进行编码。我们可以把我们喜欢的两首歌编成编码，听两首歌曲之间的不同插值。或者如Magenta团队展示了他们的NSynth项目，我们可以在不同的乐器之间进行插值。

NSynth：https://magenta.tensorflow.org/nsynth

这也为我们提供了巨大的艺术上的应用。举一些很好的例子，看看hardmaru在人画草图和他的其他作品之间的插值。它使用的技术与Alice和Bob使用的技术非常相似。

Hardmaru：http://blog.otoro.net/2017/05/19/teaching-machines-to-draw/

他们发现的另一个有趣的技巧是，通过修改他们的训练过程，他们实际上可以给一个或多个代码维度赋予特定的含义。这类似于我们在part 1中讨论的简单的dog/cat和black/white代码，其中两个维度人类可解释的含义。例如，他们可以用一个维度来编码胡子长度的属性。

假设他们使用的第一个维度是胡子长度，0表示没有胡须，而长度越大表示胡子越长。Alice又把自己的形象写下来。当然，Alice不是一个有胡子的女士，这对于第一个编码值是0.0。让我们假设它在这个新代码中被编码为(0.0,4.0)。Bob现在可以做一些有趣的事情了。他可以画出他会联想到的图像(X, 4.0)。较大的X，表示胡子的长度越长，保持其他代码尺寸不变，就能保持图像的“Aliceness”。所以他基本上可以准确地预测出Alice会长什么样的胡子。

对于一个真实的例子来说，看看由Xi Chen等人提出的InfoGAN所生成的数据。本文采用了一种不同的生成模型，即所谓的生成对抗性网络(GAN)，但其基本思想是相同的。艺术的状态得到了极大的改善，可以生成的图像变得更加详细和真实，但这是早期的论文先驱之一。

InfoGAN：https://papers.nips.cc/paper/6399-infogan-interpretable-representation-learning-by-information-maximizing-generative-adversarial-nets.pdf

蛮好玩的！但是玩够了。爱丽丝和鲍勃需要再次关注。他们已经有了一个新的目标！

下次，在本系列的part 3，我们将跟随他们的旅程回到自动编码的奥林匹克。这一次是讨论一个新的学科——文本编码。

参考链接：

1. VAE原始论文：https://arxiv.org/abs/1312.6114

2. http://jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf

原文链接：

https://towardsdatascience.com/the-variational-autoencoder-as-a-two-player-game-part-ii-b80d48512f46

更多教程资料请访问：人工智能知识资料全集

-END-

专 · 知