太阳耀斑环——射电微波及相关波段的研究

作者：黄光力 (中国科学院紫金山天文台)

摘要 与大多以光学波段为主的耀斑研究不同的是，作者拟以射电微波(厘米波段)的频谱和成像观测为主及相应的辐射机制研究太阳活动的基本单元——耀斑环及其物理参数的空间分布和时间演化规律。特别是中国研制的具有国际最高的时间、空间和频率分辨率的射电日像仪(MUSER)已投入运行，文章将为推动该设备即将开展的科学研究提供重要的参考工具。此外，文中也加入了与射电微波辐射密切相关的X射线、紫外和光学波段的研究，符合太阳物理乃至整个天体物理多波段研究的大趋势。文章集中介绍作者最具特色的研究，由于篇幅所限只能给出基本物理思想和概念、主要结论和代表性插图，对相应的理论推导、观测数据处理等细节，读者可根据需要参阅对应的参考文献。

关键词 太阳，耀斑，射电辐射，微波，日像仪

1 概述

耀斑是太阳爆发的主要方式之一，在几分钟到几小时内可释放10³⁰—10³²尔格的磁能，常伴有的高能粒子事件和日冕物质抛射可能穿越日地空间抵达地球，导致人造卫星、导航、通信，乃至电力运行的中断。耀斑通常表现为复杂的局部增亮的多重环状结构，为不同温度的等离子体，由植根于太阳表面(光球)的环状磁力线所约束，可在不同波段观测到，并称之为耀斑环。其中发生的物理过程有：磁力线重联触发磁能释放、带电粒子加速、传播和辐射、不同尺度的磁流体波和等离子体湍流的形成和演化等，从而成为太阳物理、等离子体物理和空间物理共同关注的目标^[1]。

射电波段是天文观测的一个重要窗口，波长从十米、米、分米、厘米(可向更长或更短扩展)几乎覆盖从太阳到地球的传播路径；观测手段从早期的单频流量计，到宽带频谱仪，进而有单频成像观测，最终走向高时间、高空间和高频率分辨的频谱日像仪^[2]。由于射电辐射的频率和射电源所在的高度有内在关联，频谱日像仪原则上可实现耀斑环的三维成像，其优势是其他波段很难具备的。在我国研制的分米—厘米波段频谱日像仪MUSER^[3]投入运行之前，日本野边山日像仪(工作频率17 和34 GHz)是国际上性能最稳定和数据利用率最高的设备之一^[4]，本文相当一部分的研究成果都是基于该设备的观测数据。

就辐射机制而言，射电微波主要来自于中等相对论电子的回旋同步辐射，而更低频率的射电辐射(分米、米以及更长波)多来自等离子体辐射及各种等离子体波和不稳定性的贡献，不在本文讨论范围内，感兴趣者可参考《等离子体动力学及其在太阳物理中的应用》^[5] 一书。

本文主要源于黄光力、V. F. Melnikov(俄)、季海生和宁宗军合作撰写的专著《耀斑环物理》^[6]，增订的英文版于2018 年由Springer 出版社出版(题为：Solar Flare Loops: Observations and Interpretations)，得到了国家科学技术学术著作出版基金的支持^[7]。

2 耀斑环中的微波辐射理论研究进展

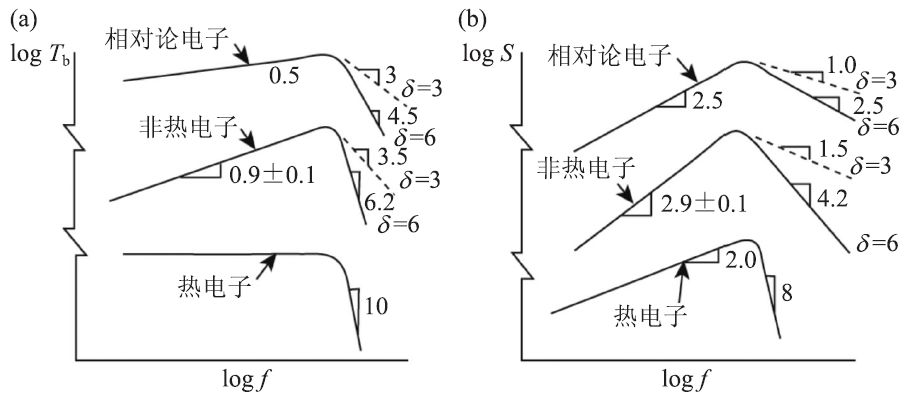
回旋同步辐射介于非相对论电子的回旋辐射和相对论电子的同步辐射之间，图1 给出了3 种情况下的亮温度谱(等效的黑体辐射温度)和流量谱的比较^[8]。通常用非热电子来区分非相对论的热电子和相对论电子。在对数坐标下的回旋同步辐射谱具有单峰，低于峰值频率一侧斜率为正(称为光学厚)，高于峰值频率一侧斜率为负(称为光学薄)。对耀斑而言我们主要关心光学薄辐射，其谱指数(即斜率)的绝对值越小高频辐射越强，称为较硬的谱，反之，则称为较软的谱。

图1 对数坐标下的回旋同步辐射谱(a)亮温度谱T_b；(b)流量谱S。电子能谱指数δ为3—6，微波谱斜率(绝对值)用直角标注，横坐标为频率f ^[8]

经典的回旋同步辐射理论由Ramaty(1969 年)奠定^[9]，之后几十年经各国太阳射电学者不断发展和完善。V. F. Melnikov 与同事合作发表系列论文着重研究Razin 效应、非热电子投射角及其在耀斑环注入位置等因素对回旋同步辐射的影响，被国际太阳物理同行所关注^[10]，并发展了高速计算程序(http://www.lmsal.com/solarsoft/ssw_packages_info.html) 及详细的使用说明(https://web.njit.edu/~gnita/gx_simulator_help/)^[11]。

(1)Razin 效应的物理本质是在等离子体折射率小于1(波的相速度大于真空光速)时，和真空(折射率等于1)情况相比，所产生的回旋同步辐射受到很强的抑制，特别是在较低的频率(光学厚区)，与回旋同步辐射的自吸收共同影响辐射谱的形状、峰值频率和谱指数。对Razin 效应而言，可从相对论电子的Lienard—Wiechert(推迟)势函数的分母在真空趋于零，而在等离子体中偏离零值来直观地理解，所以Razin 效应并非是通常意义下的吸收机制。

(2)经典理论通常假设电子投射角分布是各向同性的，大量数值计算表明电子投射角的各向异性对辐射性质有显著影响。我们从经典理论导出图1 中光学薄谱指数α和产生辐射的电子能谱指数δ之间存在某种关系(如α=0.9δ－1.22)^[8]，而在投射角各向异性的情况下将会明显偏离上述关系；投射角各向异性还有可能导致谱指数的振荡乃至偏振极性的反转，预期对未来研究耀斑环中不同位置辐射谱的分布和电子谱的诊断有重要的意义。

此外，我国学者周爱华将回旋同步辐射理论从厘米推广到毫米波段也是值得关注的^[12]。

3 耀斑环微波辐射的观测及其解释

这部分是文章要重点介绍的内容。首先从没有空间分辨的观测研究微波爆发谱的峰值频率的变化及其原理解释，以及微波爆发的发生率和频率的统计关系及其对雪崩模型的修正；进而利用有空间分辨的观测研究发现，相当一部分环顶辐射强于环足，首次发现一类硬软硬的微波谱的演化特征，以及足点辐射的不对称性和偏振极性及相应的物理解释。分别介绍如下。

(1)对美国欧文斯谷太阳射电阵(OVSA，1—18 GHz)观测的34 个简单脉冲爆发的统计发现：60%—80%的峰值频率和爆发强度成正相关，可用回旋同步辐射的自吸收解释；同时30%—36%的峰值频率在爆发中基本保持不变，可能是Razin 效应使得低频射电源变为光学薄抵消了自吸收的影响；此外，还有70%的爆发的下降阶段在某一时刻开始出现峰值频率上升及高频谱的变硬，均可用Razin 效应来解释^[13]。

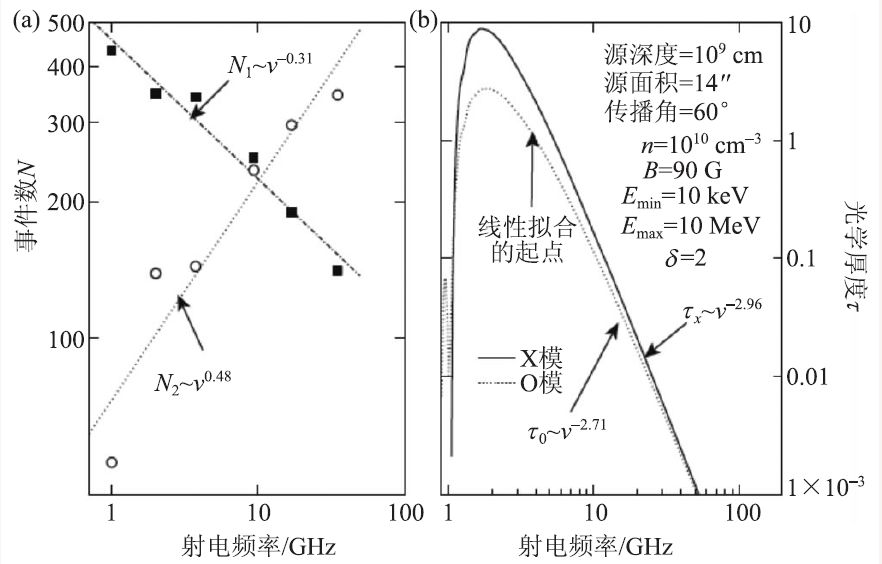
(2)不同波段的统计证实，耀斑发生率和强度满足指数约为1.8 的幂律分布，符合非线性雪崩模型的预期^[14]，上述统计的缺陷是对偏离幂律分布的小事件的低端截止的任意选择。为此我们用改进后的最大似然法^[15]，按严格的数学标准选取低端截止，分析了日本野边山偏振计(1—35 GHz)观测的486 个爆发，发现满足幂律分布的事件数随着频率增大而上升，即光学薄区有更多事件反映耀斑能量释放的特征(图2)。进而发现幂律指数随频率增大逐渐变小(1.95—1.75)，低频端斜率接近于满足微耀斑加热日冕的理论要求^[16]。

图2 (a)满足和偏离幂律分布的事件数(N₂和N₁)随频率变化；(b)回旋同步辐射光学厚度τ随频率变化(n为等离子体密度，B为磁场，E_max和E_min为电子能量的上下限)^[16]

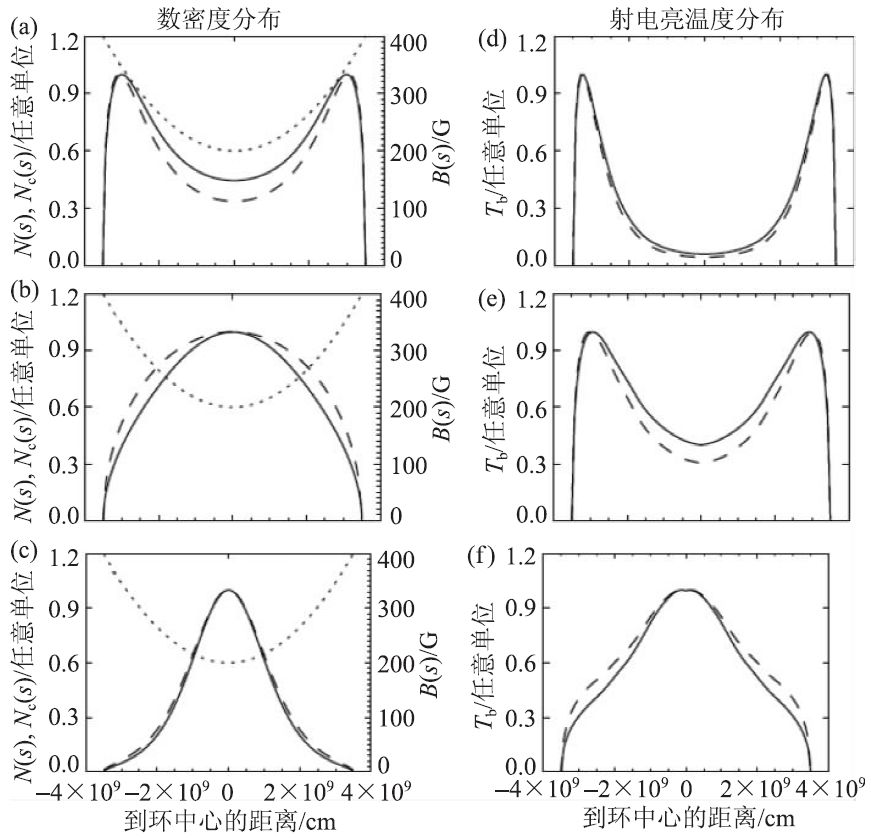
(3)由于微波辐射随源区磁场强度增大^[8]，通常认为耀斑环的足点辐射强于环顶。我们对日本野边山日像仪的个例和统计研究发现，相当一部分(约40%)爆发峰值时刻环顶光学薄辐射强于环足^[17]，其原因很可能是由于环顶的非热电子密度明显高于环足(图3(c)，(f))。进一步求解电子密度满足的福克尔—普朗克方程发现，当非热电子的加速和注入位置在环顶附近时可以解释这一新的观测现象^[18]。

图3 左列给出电子密度的3 种沿耀斑环的分布：(a)类束流，(b)损失锥和(c)馅饼(右侧纵坐标为磁场强度)。右列为对应3 种分布的射电微波光学薄(34 GHz)亮温度分布T_b的理论计算值。实线和虚线分别表示密度N和柱密度N_c，点线表示磁场强度B^[18]

(4)耀斑环的足点的微波辐射不对称性是普遍存在的，传统的解释是由于磁镜不对称和辐射强度依赖于当地磁场。我们的统计发现，辐射强度和足点磁场的不对称性没有相关性，足点辐射的不对称很可能是由于非热电子初始投射角的不对称所造成^[19]。

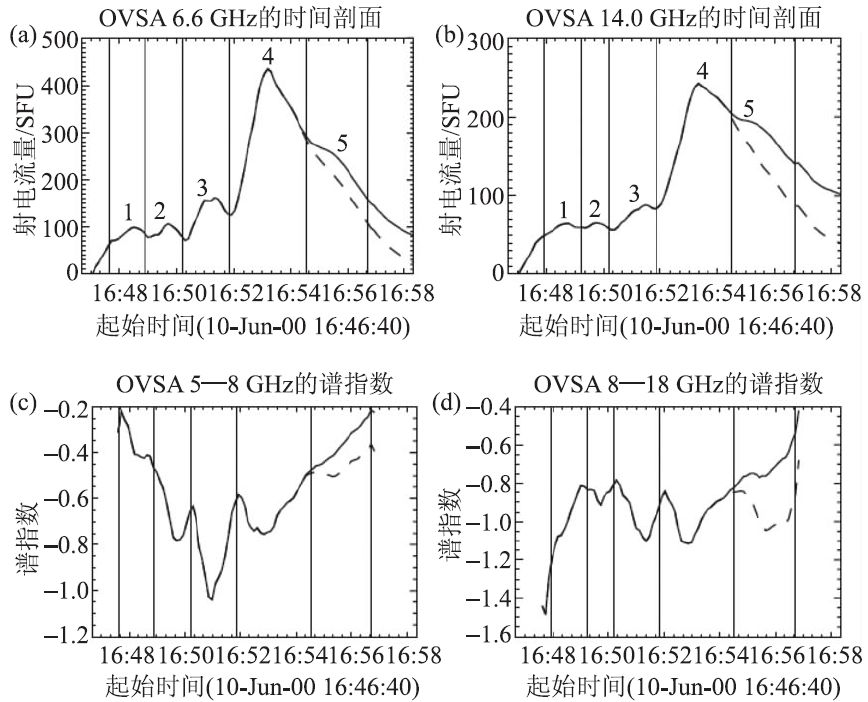
(5)关于微波爆发谱指数演化的软硬软或软硬硬特征，通常用辐射谱和电子谱同步演化以及磁镜的捕获效应导致爆发后期高能电子数增加(变硬)来解释。我们首次发现一类新的演化特征——硬软硬(图4)^[20]。有趣的是，这一类事件均具有精细结构，爆发的整体和每一个精细结构脉冲与谱指数均具有负相关，即谱指数演化具有硬软硬的特征。初步解释为非热电子多次注入，捕获效应导致电子谱变硬^[21]，下次入射时电子谱回软，如此周而复始。值得注意的是，硬软硬的特征在低频段更为明显(比较图4 左右两列)，在高频段(耀斑环底部)由非热电子重复注入所产生的精细结构在向下传播的过程中逐渐被平滑。

图4 (a，b)OVSA在低频(6.6 GHz)和高频(14 GHz)的流量时变曲线；(c，d)对应的低频段谱指数(5—8 GHz)和高频段谱指数(8—18 GHz)的演化曲线。一组垂直线段将上述时变曲线分割成5 个精细结构对应的小脉冲。图中的虚线是在扣除热的轫致辐射之后的结果，其中，源区温度由日本阳光卫星的软X射线望远镜数据获取^[20]

(6)对微波辐射足点偏振的统计研究发现，多数情况下具有相同的偏振极性。与传统的磁场极性相反导致其偏振极性相反的观点不符，表明线性模转换的弱耦合产生偏振极性翻转是普遍存在的^[22]。可以从观测确认弱耦合的两个必要条件是否满足：电磁波穿越准横区和辐射频率小于弱耦合的临界频率^[23]。

4 耀斑环中的X 射线辐射理论进展

尽管由轫致辐射激发X射线的经典理论已经成熟，但仍有需要完善之处。比如，非热电子低能截止的变化可能导致熟知的厚靶和薄靶公式的失效；非热电子进入耀斑环后分解为捕获和沉降两部分，其比例是由磁镜镜比和电子初始投射角共同决定；电子投射角各向异性对X射线属性的影响等，下面将逐一介绍。

(1)硬X 射线的轫致辐射预期电子谱指数等于辐射谱指数减1(薄靶)或加1(厚靶)，成为目前诊断非热电子谱的基本公式^[24]。我们发现，上述关系只有在非热电子的低能截止小于光子能量的条件下成立，计算表明只有在低能截止小于20 keV 的情况下方可使用上述关系。比如，当低能截止等于50 keV时，电子谱指数为7 的厚靶辐射谱指数从标准模型的6 偏离到4.3，这种偏离随电子谱指数增大而增大，随光子能量增大而减小^[25]。

(2)耀斑环中的非热电子由于磁矩守恒分解为(逃逸)沉降和捕获电子两种成分，分别激发硬X射线和微波辐射。我们借助于核聚变等离子体理论，求解非热电子所满足的福克尔—普朗克方程，根据两种成分在速度空间的边界条件、入射电子的幂律分布和任意投射方向，导出沉降和捕获电子分布的解析表达式。一个重要的推论是：沉降和捕获电子数之比取决于镜比和初始投射角两个因素，即沉降电子随镜比和初始投射角增大而减少，捕获电子随镜比和初始投射角增大而增加^[26]。在以往研究中通常只考虑磁镜而忽略了初始投射角的影响。

(3)和微波辐射类似，首次强调电子入射角各向异性对X 射线辐射强度、方向性和偏振的影响，预期对今后研究耀斑环中的X射线辐射有重要的意义^[27]。

5 耀斑环X 射线辐射的观测及其解释

由于X射线和微波辐射密切相关，作为比较研究，以下将分别介绍耀斑环顶部和足点的谱指数关系及其对应的辐射机制；首次发现X射线爆发中的谱指数所具有的硬软硬特征，及其对能量和位置的依赖性；以及足点的X 射线辐射不对称性。

(1)耀斑环顶部和环足的X射线辐射来自同源的非热电子，其属性应具有明显的相关性。我们对RHESSI 卫星观测的28个耀斑环样本进行统计分析，发现环顶和环足谱指数的相关性可分成两组，分别具有正相关和负相关，与前人一致的是环顶谱指数总是比环足软，两者之差对正相关组为2—4，对负相关组为0—2，后者恰好符合薄靶(软)和厚靶(硬)的理论差值，前者则必须考虑热辐射的贡献。进而分别对环顶和环足的光子流量和谱指数进行相关分析，发现环足满足负相关(符合轫致辐射和热辐射的理论预期)，而环顶同样可以分为正相关和负相关两组，且两次分组的界限都是在谱指数为4.5 附近。我们采用RHESSI 卫星软件包含的薄靶程序进行计算，发现随非热电子低能截止增大在谱指数为4.5 附近确实出现正负两种相关性，可以很好地解释上述观测现象^[28]。

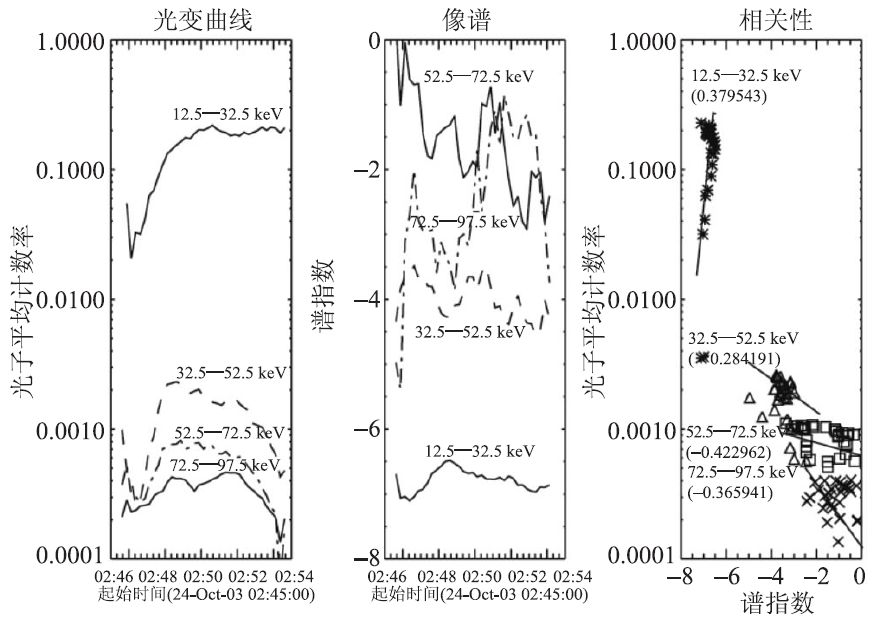
(2)和微波辐射类似，硬X射线辐射谱在高能段的演化出现了硬软硬的新特征，在较低能段仍保持熟知的软硬软，可分别从图5 中光子数和谱指数分别呈负相关和正相关来确认，同样可用捕获效应解释。上述数据选自RHESSI 卫星的成像观测，环顶的捕获效应明显强于环足^[29]。此外，硬X射线的回流和光球反射等物理效应也是上述现象的可能的解释。

图5 2003 年10 月24 日耀斑环顶不同能段的时变、谱指数演化及其相关性^[29]

(3)耀斑环足X射线辐射的不对称性前人已有关注，大多用磁镜不对称来解释，即磁场较强的足点沉降电子数量较少，故X射线辐射较弱。但仍有少量事例的不对称性恰好与磁镜效应预期相反，以及随时间、能量变化等复杂情况；另外，双环和多环结构经常出现，通常是一个致密磁环位于另一大尺度磁环的具有较强磁场的足点附近，致密环的足点具有较强的X射线辐射，微波辐射则出现在具有较弱磁场的大环足点。以上反常结果都是磁镜效应无法解释的。我们利用前面导出的沉降电子分布函数，当非热电子加速位置较高时可解释反常的环足不对称性，对于双环相互作用的上述情形，考虑镜比和电子投射角的联合效应也可得到合理的解释^[26]。

6 耀斑环物理参数的诊断

辐射机制不仅可用来正向的解释观测，还可反向的推测未知的源参量，特别重要的是，目前尚无法直接测量的耀斑环磁场和非热电子参量(截止能量和投射角等)，将有助于理解耀斑环中发生的物理过程。

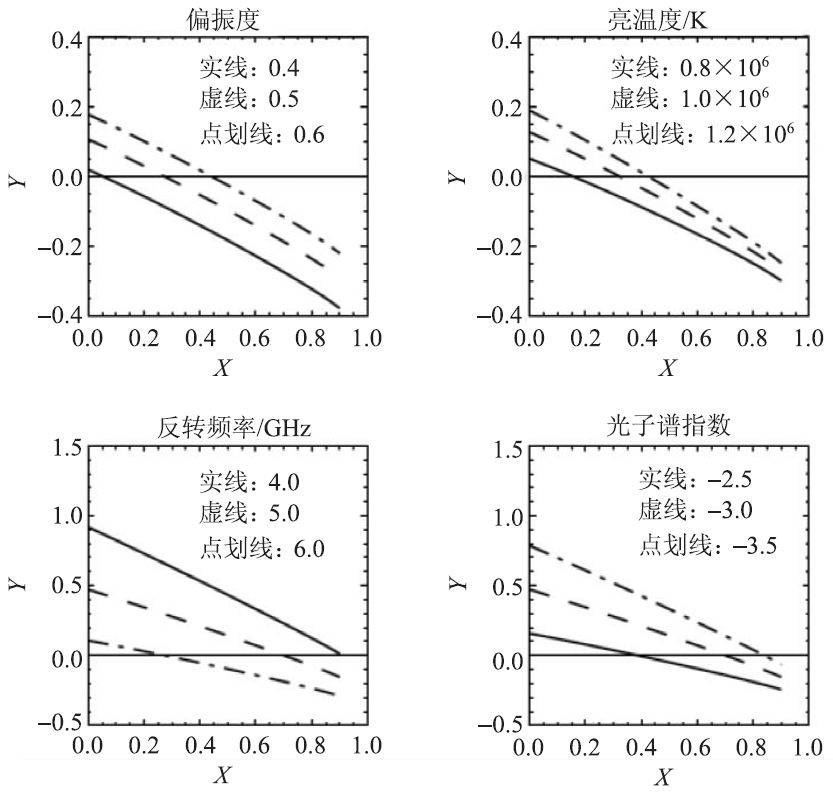
(1)因日冕的线辐射及其塞曼效应很弱，背景磁场成为耀斑环最为重要却无法直接测量的物理参数^[30]。从回旋同步辐射理论的近似拟合^[31]和微波爆发的峰值频率、亮温度和光薄谱指数，可以导出源区磁场强度和非热电子密度的解析式^[32]，进而计入微波辐射的偏振度即可得到磁场和视线方向的夹角，从而计算磁场在平行和垂直于视线方向的两个分量^[33]。图6 给出该夹角余弦所满足的非线性方程的数值解，对偏振度、亮温度、反转(峰值)频率，和光学薄谱指数的典型值满足存在唯一性(曲线和Y=0 的直线交点对应的X值)^[22]。对于有时空分辨能力的日像仪而言，可以直接得到微波爆发源区磁场的空间分布和时间演化；对于MUSER这样具有频率分辨能力的频谱日像仪而言，我们还可计算不同频率对应的爆发源区高度的磁场，从而实现日冕磁场的三维重构，并且可与光球磁场外推进行比对。进一步对若干具体事件的研究表明：日冕磁场横向分量的大小和变化范围远超纵向磁场，支持爆发能量主要来自横向磁场的观点^[34]。注意上述诊断受到若干近似条件的限制，可从更严格的理论导出日冕磁场的数值解^[22]。

图6 从偏振度、峰值频率、亮温度和光学薄谱指数计算磁场和视线方向的夹角^[22]

(2)非热电子的加速通常具有能量下限即所谓低能截止(等离子体物理称之为逃逸限)，在观测到的硬X射线能谱中表现为低能端变平(偏离幂律分布)，成为研究非热电子加速的重要参量。由于光球的康普顿散射同样会造成低能端变平，低能截止是否存在曾被质疑^[35]；然而，RHESSI卫星的大样本统计表明，即使扣除康普顿散射仍不能排除低能截止的存在^[36]。

现有的诊断低能截止有几种方法：轫致辐射理论拟合观测^[37]、不同时刻的光子谱的共同交点可能给出低能或高能截止^[38]、相邻能段辐射强度比值拟合观测^[39]、严格的辐射理论反演等^[25]，所得到的低能截止有较大的变化范围。

(3)如前所述，微波和硬X射线辐射与非热电子初始投射角密切相关，在爆发源区磁场诊断的基础上，可以进一步诊断耀斑环两个足点的非热电子初始投射角(之比)^[17]。

7 耀斑环的整体行为

以上侧重研究的是耀斑环中的微观物理过程(辐射机制、非热电子的加速和传播等)和对应的观测现象。下面将介绍一些耀斑环的大尺度的整体行为，例如耀斑环的膨胀和收缩、耀斑环的准周期振荡、耀斑环的相互作用、耀斑环中的色球蒸发等现象的研究进展。

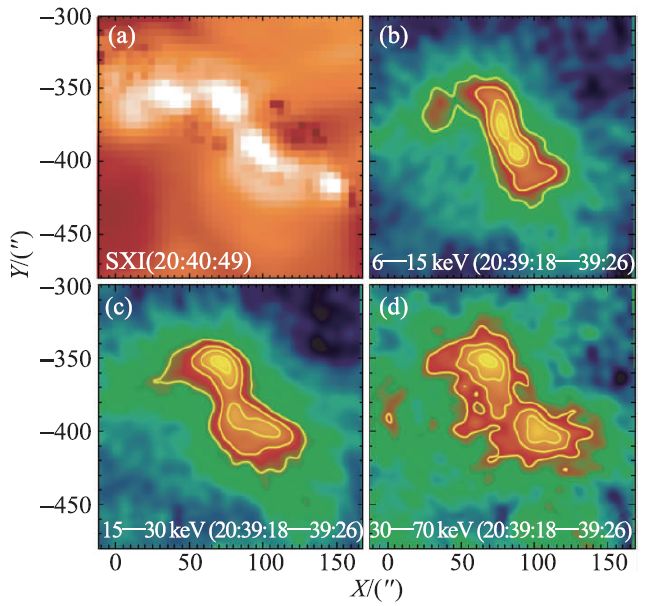
(1)耀斑环在爆发期间的不断膨胀已为大量观测所证实，可用磁重联位置随磁绳或暗条不断上升来解释。季海生等利用美国大熊湖天文台高分辨观测发现Hα亮核距离在耀斑上升期间减少，过了极大相之后开始增大，与此同时硬X射线的足点运动也有类似的规律^[40]，进而提出耀斑足点的汇聚和分离是一种退剪切运动^[41]，首次发现这种运动与X射线之字型结构(Sigmoid)同时出现(图7)^[42]，在野边山日像仪的观测中也有类似的现象^[43，44]。

图7 2003 年10 月29 日观测到的X射线之字型结构^[42]

(2)耀斑环的准周期振荡在光学、X射线、紫外和微波段被观测到，并携带有关能量释放、触发机制和粒子加速等重要信息(详参评述文章^[45])。当调制深度较大时，可视为一系列准周期元爆发的组合，其重复率R 和爆发本底流量S 之间满足S=UR+b 的准量子化能量释放的关系，即单个爆发释放的能量U近似为常数^[46]；从日本野边山偏振计(1—35 GHz)观测发现，能量U的极大值在10 GHz附近，表明在该频率对应的高度耀斑活动可能比较剧烈，与雪崩模型的统计结果可比^[47]。

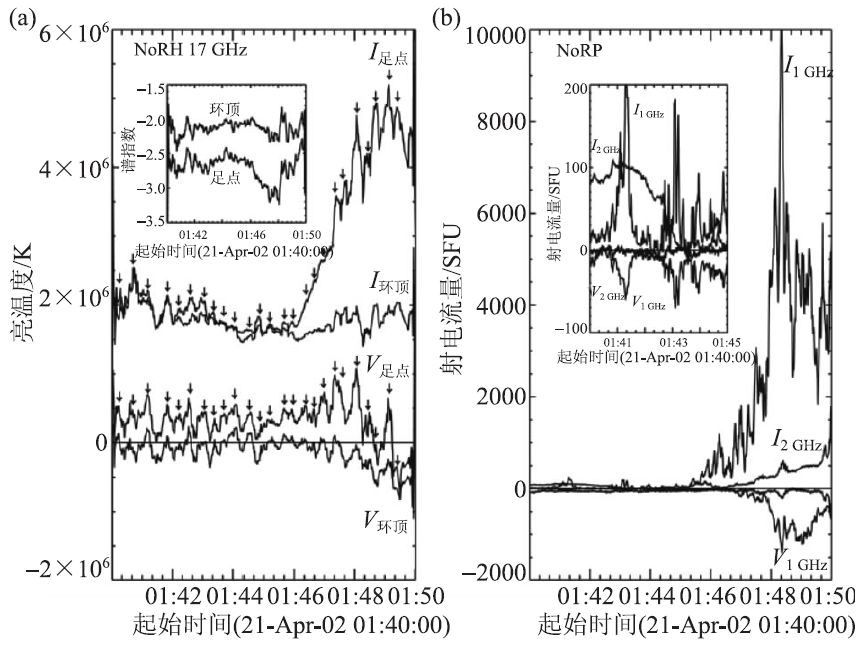
(3)耀斑环相互作用是重要的耀斑触发机制。2002 年4 月21 日X 级耀斑前期的多波段观测发现，耀斑环系从日面边缘向外膨胀，环顶处发生剧烈碰撞和局部增亮。有趣的是，环足的微波偏振极性保持正常的右旋极性，而环顶偏振在零点附近振荡最终反转为左旋(图8)，同时辐射强度和偏振时变的反相关表明耀斑能量释放和源区磁场的内在关系^[48]。

图8 2002 年4月21 日野边山日像仪(a)和偏振计(b)的强度和偏振观测^[48]

(4)由于日冕和色球的温度密度均有数量级的差异，色球蒸发在耀斑能量的积累、传输和释放过程中发挥重要的作用。色球蒸发在光谱观测中表现为高速等离子体外向流(蓝移)，有时伴随色球凝聚即等离子体内向流(红移)。文献[7]中有专门章节介绍近年来色球蒸发的观测和理论研究进展(还可参考文献[49，50])。

8 总结

太阳无可争辩的是与我们关系最为密切的一颗星球，不仅带来了人类生存所必需的光和热，太阳大气磁场的活动还可能直接影响当代航天航空乃至电力通讯，从而产生空间天气学这样一门新兴学科。同时，太阳又是人类唯一可以近距离观测的恒星，作为组成宇宙的基本单元，决定了太阳物理的研究在现代天文学中所占有的特殊位置。太阳活动的主要形式(耀斑、日冕物质抛射、高能粒子事件等)的发生与太阳大气磁场的环状结构(即耀斑环)有密切关系。由于历史的原因，耀斑观测以光学波段为主，而射电观测近年来逐渐显示其独特的优越性。作者希望通过本文让物理界同行、研究生和本科生更多地了解、关注乃至投入这一方面的研究。

参考文献

[1] 方成，丁明德，陈鹏飞. 太阳活动区物理. 南京：南京大学出版社，2008

[2] 谭宝林，程俊，谭程明等. 天文学报，2018，59：37-1

[3] Yan Y，Zhang J，WangWet al. EM&P，2009，104：97

[4] Nakajima H，Nishio M，Enome S et al. Proc. IEEE，1994，82：705

[5] 黄光力. 等离子体动力学及其在太阳物理中的应用——现代太阳物理丛书. 北京：科学出版社，2009

[6] 黄光力，Melnikov V F，季海生等. 耀斑环物理. 北京：科学出版社，2016

[7] Huang G L，Melnikov V F，Ji H S et al. Solar Flare Loops: Observations and Interpretations. Singapore：Springer，jointly with Beijing：Science Press，2018

[8] Dulk G A. Annual Rev. Astron. Astrophys.，1985，23：169

[9] Ramaty R. Astrophys. J.，1969，158：753

[10] Melnikov V F，Gorbikov S P，Pyatakov N P. Formation of anisotropic distributions of mildly relativistic electrons in flaring loops. Proceedings of the International Astronomical Union，IAU Symposium，2009，Volume 257，p. 323-328

[11] Fleishman G D，Kuznetsov AA. Astrophys. J.，2010，721：1127

[12] Zhou A H，Li J P，Wang X D. Research in Astron. and Astrophys.，2016，16：31

[13] Melnikov V F，Gary D E，Nita G M. Solar Phys.，2008，253：43

[14] Charbonneau P，McIntosh SW，Liu H L et al. Solar Phys.，2001，203：321

[15] Song Q，Huang G，Tan B. Astrophys. J.，2012，750：160

[16] Song Q，Huang G，Huang Y. Astrophys. Space Sci.，2013，347：15

[17] Huang G L，Nakajima H. Astrophys. J.，2009，696：136

[18] Melnikov V F，Shibasaki K，Reznikova V E. Astrophys. J.，2002，580：L185

[19] Huang G L，Song QW，Huang Y. Astrophys. J.，2010，723：1806

[20] Song Q W，Huang G L，Nakajima H. Astrophys. J.，2011，734：113

[21] Metcalf T R，Alexander D. Astrophys. J.，1999，522：1108

[22] Huang G，Song Q，Li J. Astrophys. Space Sci.，2013，345：41

[23] Cohen M H. Astrophys. J.，1960，131：664

[24] Brown J. Solar Phys.，1972，26：441

[25] Huang G L. Solar Phys.，2009，257：323

[26] Huang G L. New Astron.，2007，12：483

[27] Melnikov V F，Charikov Y E，Kudryavtsev I V. Geomagn. Aeron.，2015，55：983

[28] Shao C，Huang G. Astrophys. J.，2009，691：299

[29] Huang G L，Li J P. Astrophys. J.，2011，740：46

[30] 黄光力. 日冕磁场的射电诊断，10000 个科学难题——天文学卷. 北京：科学出版社，2010. 59

[31] Dulk G A，Marsh K A. Astrophys. J.，1982，259：350

[32] Zhou A H，Karlicky M. Solar Phys.，1994，153：441

[33] Huang G L. Solar Phys.，2006，237：173

[34] Huang G L，Li J P，Song Q W. Research in Astron. Astrophys.，2013，13：215

[35] Kontar E P，MacKinnon A L，Schwartz R A et al. Astron. Astrophys.，2006，446：1157

[36] 韩钢，李友平，甘为群. 天文学报，2008，49：403

[37] GanWQ，Li Y P，Chang J. Astrophys. J.，2001，552：858

[38] Huang G L. Solar Phys.，2000，196：395

[39] Zhang J，Huang G L. Astrophys. J.，2003，592：L49

[40] Ji H，Wang H，Goode P R et al. Astrophys. J.，2004，607：L55

[41] Ji H，Huang G，Wang H et al. Astrophys. J.，2006，636：L173

[42] Ji H，Wang H，Liu C et al. Astrophys. J.，2008，680：734

[43] Li Y P，GanWQ. Astrophys. J.，2005，629：L137

[44] Reznikova V E，Melnikov V F，Shibasaki K et al. Astrophys. J.，2009，697：735

[45] Nakariakov V M，Melnikov V F. Space Science Rev.，2009，149：119

[46] Sturrock P A，Kaufmann P，Moore R L et al. Solar Phys.，1984，94：341

[47] Huang G，Song Q. Solar Phys.，2010，264：345

[48] Huang G L，Lin J. Astrophys. J.，2006，639：L99

[49] Ning Z，CaoW. Astrophys. J.，2010，717：1232

[50] Zhang Q M，Li D，Ning Z J et al. Astrophys. J.，2016，827：27

本文选自《物理》2019年第4期

---

▼

往期精彩回顾

▼

1.环形正负电子对撞机：物理、技术以及现状

2.量子十问之六：量子计算，这可是一个颠覆性的新技术 | 郭光灿

3.晶体几何系列之二：平面上圆密排定理的证明

4.单纯的元素，复杂的历史

5.原位电子显微学探索固体中的离子迁移行为（一）

6.爱因斯坦的物理学成就与年谱 | 曹则贤

7.物理学：A Source of Power for Man

8.回音壁模式光学微腔传感

9.杨-米尔斯理论说了啥？为什么说这是杨振宁超越他诺奖的贡献？

10.周末讲堂——三位新晋狄拉克奖得主：开宗立派又风格迥异