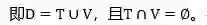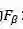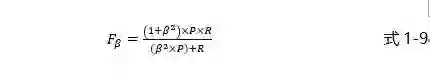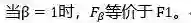博客 | TensorFlow系列专题(二):机器学习基础
本文原载于微信公众号:磐创AI(ID:xunixs),AI研习社经授权转载。欢迎关注磐创AI微信公众号及AI研习社博客专栏。
目录:
数据预处理
归一化
标准化
离散化
二值化
哑编码
特征工程
特征提取
特征选择
模型评估方法
留出法
交叉验证法
自助法
模型性能度量
正确率(accuracy)和错误率(error rate)
查准率(precision)、查全率(recall)与F1
参考文献
一.数据预处理
数据预处理的方式较多,针对不同类型的数据,预处理的方式和内容也不尽相同,这里我们简单介绍几种较为常用的方式:
(1)归一化
归一化是对数据集进行区间缩放,缩放到[0,1]的区间内,把有单位的数据转化为没有单位的数据,即统一数据的衡量标准,消除单位的影响。归一化之后的数据处理起来更方便,同时也能加快程序运行时的收敛速度。
(2)标准化
标准化是在不改变原数据分布的前提下,将数据按比例缩放,使之落入一个限定的区间,使数据之间具有可比性。标准化的目的是为了方便数据的下一步处理,比如:进行数据的缩放等变换。常用的标准化方法有z-score标准化、Min-max标准化等。
(3)离散化
离散化是把连续的数值型特征进行分段,将落在每一个分段内的数据赋予一个新的统一的符号或数值。可采用相等步长或相等频率等方式进行离散化。离散化有时是为了适应模型的需要,同时离散化也有助于消除一些异常数据,以及提高算法的效率等。
(4)二值化
二值化处理是将数值型数据转换为0和1两个值,例如通过设定一个阈值,当特征的值大于该阈值时,转换为1,小于或等于该阈值时转换为0。二值化的目的在于简化数据,有些时候还可以消除数据中的“杂音”,例如图像数据。
(5)哑编码
哑编码又称为独热编码(One-Hot Encoding),其作用是将特征进行量化。例如某个特征有三个类别:“大”、“中”和“小”,要将这一特征用于模型中,我们必须将其数值化,一个很容易想到的方式是直接给它们编号“1”、“2”和“3”。这种方式存在一个问题,即引入了额外的关系(例如数值间的大小关系),这可能会“误导”模型的优化方向。一个更好的方式就是使用哑编码,例如“大”对应编码“100”,“中”对应编码“010”,“小”对应编码“001”。如果将其对应到一个三维的坐标系中,每个类别对应一个点,且三个点之间的欧氏距离相等,均为根号2。
二.特征工程
特征工程的目的是把原始的数据转化为我们的模型可以使用的数据,其主要包括三个子问题,特征构造、特征提取和特征选择。特征构造一般是在原有特征的基础上做一些“组合”操作,例如对原有特征进行四则运算,从而得到新的特征。特征提取是指使用映射或变换的方法将维数较高的原始特征转换为维数较低的新的特征。特征选择即从原始的特征中挑选出一些最具有代表性,使得模型效果最好的特征。其中特征提取和特征选择最常使用。
(1)特征提取
特征提取又叫作“降维”,目前对于线性特征的提取,常用方法有主成分分析(PrincipleComponent Analysis,PCA)、线性判别分析(LinearDiscriminant Analysis,LDA)以及独立成分分析(Independent Component Analysis,ICA)。
① 主成分分析(Principle Component Analysis,PCA)[1]
主成分分析(PCA)是一种经典的无监督降维方法,它的主要思想是在降维的过程中实现“减少噪声”和“去冗余”从而达到降维的目的。具体来说,“减少噪声”是指在将维数较高的原始特征转换为维数较低的新特征的过程中保留下维度间相关性尽可能小的特征维度,这一操作实际上是通过借助协方差矩阵的原理所实现的;“去冗余”是指把“减少噪声”操作之后保留下来的维度再进一步筛选,去掉含有较小“特征值”的维度,使得留下来的特征维度含有的“特征值”尽可能的大,特征值越大方差就会越大,进而所包含的信息量就会越大。(注:关于为什么通过借助协方差原理可以实现将维数较高的原始特征转换为理想的维数较低的新特征,也就是特征提取,不在本书的讨论范围内)。
主成分分析(PCA)法一大特点就是它是完全无参数限制的,也就是说PCA的结果只与数据有关,而用户是无法进行干预的。这是它的优点,同时也是缺点。针对这一特点,PCA核方法kernel-PCA后来被提出,使得用户可以根据先验知识预先对数据进行非线性转换,它也是当下比较流行的方法之一。
② 线性判别分析(Linear Discriminant Analysis,LDA)[2]
线性判别分析(LDA)是一种经典的有监督降维算法,它的主要思想是借助协方差矩阵、广义瑞利熵等原理实现数据类别间距离的最大化和类别内距离的最小化。了解了其主要思想,那么线性判别分析(LDA)又是怎样实现的呢?这里以二分类LDA为例,二维特征通过一系列矩阵运算实现从二维平面到一条直线的投影,期间同时通过借助协方差矩阵、广义瑞利熵等实现类间数据的最大化与类内数据的最小化。从二分类推广到多分类是在二分类的基础上增加了“全局散度矩阵”来实现最终目标优化函数的设定,从而实现类间距离的最大化和类内距离的最小化。显然,由于它是针对各个类别做的降维,所以数据经过线性判别分析(LDA)降维后,最多只能降到原来的类别数减一的维度。
正因为如上特性,线性判别分析(LDA)除了可以实现降维外还可以实现分类[3]。另外,对比前文讲的主成分分析(PCA)可以看出,LDA在降维过程中着重考虑分类性能,而PCA着重考虑特征维度之间的差异性与方差的大小即信息量的大小。
③ 独立成分分析(Independent Component Analysis,ICA)[4]
独立成分分析(ICA)的主要思想是在降维的过程中保留相互独立的特征维度。这比PCA更进一步,在保证特征维度之间不相关的同时保证相互独立。不相关只是保证了没有线性关系,而并不能保证是独立的。
正因为其是以保证特征维度之间的相互独立性为目标,独立成分分析(ICA)往往会比PCA有更好的降维效果。独立成分分析(ICA)目前已经广泛的应用到数据挖掘、图像处理等多个领域。
(2)特征选择
不同的特征对模型的影响程度不同,我们要选择出重要的一些特征,移除与问题相关性不是很大的特征,这个过程就叫做特征选择。特征选择的最终目的是通过减少冗余特征以达到减少过拟合、提高模型准确度和在一定程度上减少训练时间的效果。对比前文介绍的特征提取,特征选择是对原始特征取特征子集的一个操作,而特征提取则是对原始特征进行映射或者变换操作以得到低维的新特征。
特征的选择在特征工程中十分重要,往往可以很大程度上决定最后模型训练结果的好坏。常用的特征选择方法有:过滤式(filter)、包裹式(wrapper)以及嵌入式(embedding)。
① 过滤式
过滤式特征选择一般是通过统计度量的方法评估每个特征和结果的相关性,来对特征进行筛选,留下相关性较强的特征。其核心思想是:先对数据集进行特征选择,然后再进行模型的训练。即过滤式特征选择是独立于特定的学习算法的。也正因如此,过滤式特征选择拥有较高的通用性,可适用于大规模数据集。同样地,正是由于其独立于特定的学习算法,也造成了其在后面的模型表现即分类准确率方面可能会表现欠佳。常用的过滤式特征选择方法有Pearson相关系数法、方差选择法、假设检验、互信息法等。这些方法通常是单变量的。
② 包裹式
包裹式特征选择通常是把最终机器学习模型的表现作为特征选择的重要依据,一步步筛选特征。这种一步步筛选特征的过程可以看作是目标特征组合的搜索过程,这种搜索过程可以是最佳优先搜索、随机爬山算法等。目前比较常用的一种包裹式特征选择法为递归特征消除法,其原理是使用一个基模型(如:随机森林、逻辑回归等)进行多轮训练,每轮训练结束后,消除若干权值系数较低的特征,再基于新的特征集进行新的一轮训练。
正是由于包裹式特征选择是根据最终的模型表现来选择特征的,故通常其要比前文提到的过滤式特征选择有着更好的模型表现。同样的,由于训练过程时间久,系统的开销也更大,一般来说不太适用于大规模数据集。
③ 嵌入式
嵌入式特征选择同样是根据机器学习的算法、模型来分析特征的重要性,从而选择比较重要的N个特征。与包裹式特征选择法最大的不同是,嵌入式方法是将特征选择过程与模型的训练过程结合为一体,这样就可以快速地找到最佳的特征集合,更加高效、快捷。简而言之,嵌入式特征选择是将全部的数据一起输入模型中进行训练和评测,而包裹式特征选择一般是一步步筛选特征,一步步减少特征进而得到所需要的特征维度。常用的嵌入式特征选择方法有基于正则化项的特征选择法(如:Lasso)和基于树模型的特征选择法(如:GBDT)。
三.模型评估方法
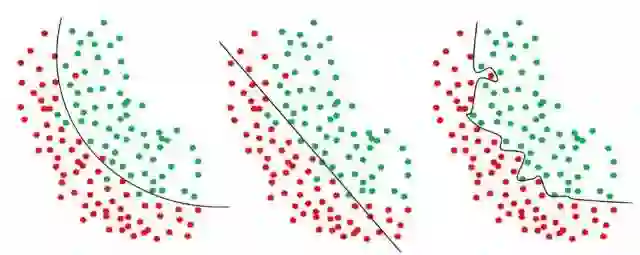
对于训练得到的模型,我们肯定希望它在新的数据上也总是能够表现出很好的性能,所以我们希望模型能够尽可能多的学习到训练数据的特征。在机器学习中有两个常见的现象,分别是“过拟合”和“欠拟合”。当模型把训练数据的特征学习的“太好”的时候,往往会出现“过拟合”的现象,与之相对应的就是“欠拟合”,即模型没有学习好训练数据的特征。图1-4是一个简单的例子。
图一 “过拟合”和‘’欠拟合‘’示例(从左至右依次为:理想情况、欠拟合和过拟合)
无论是“过拟合”还是“欠拟合”,这都不是我们希望看到的。“欠拟合”通常是由于模型过于简单或者学习不够充分等等原因导致的,相对来说也比较容易解决。而“过拟合”一般是由于数据中的“噪声”、或者是模型将训练数据特有的一些特征当成了该类数据都会具有的一般特征,通常在训练数据过少、模型过于复杂或者参数过多的时候容易出现“过拟合”问题。
为了得到一个效果最好的模型,我们通常会选择多种算法,对于每种算法都会尝试不同的参数组合,并比较哪一种算法、哪一种参数设置更好,这就是模型的选择。为了比较这些模型的优劣,我们需要有一些相应的评估方法和评价标准。这里我们先来介绍一些常用的模型评估的方法,后面的内容里我们会接着介绍模型评价的一些标准,又称为模型的“性能度量”。
在介绍具体的模型评估的方法之前,我们需要先弄清楚几个简单的概念。第一,我们常说的“参数”和“超参数”分别指什么?第二,“训练集”、“测试集”和“验证集”怎么划分?
首先,什么是“参数”和“超参数”?这里的“参数”既是我们的模型需要学习的内容,它是模型“内部”的变量,比如模型的权重矩阵和偏置。而超参数是指在一个模型中,我们可以人为设定和修改的参数,例如神经网络的层数、学习率以及隐藏层神经元的个数等等。模型的选择除了选择具体的模型外(例如是选择LSTM还是选择Bi-LSTM),还需要选择模型的“超参数”。
“训练集”、“测试集”和“验证集”的划分是模型的选择和训练过程中的一个重要环节。可能有部分读者对“测试集”和“验证集”的关系不是很清楚。“测试集”的作用很好理解,当我们训练好了一个模型之后,我们想要知道这个模型的泛化能力好不好,这时候我们可以用模型在“测试集”上的表现来近似评价模型的泛化能力。那么“验证集”又是什么呢?举个简单的例子:假设我们有一个训练集A和一个测试集B,两个数据集没有重叠。当我们在进行模型的选择的时候,我们用训练集A来训练模型,然后用测试集B来评估模型的“好坏”。这个时候可能会出现一种问题,由于我们是以模型在测试集B上的表现来评价模型的“好坏”,所以我们最后选择的模型可能刚好在测试集B上的表现比较好,这就是我们常说的“过拟合”。那么要如何避免这种问题呢?方法就是再增加一个“验证集”,在选择模型的时候,我们使用“验证集”来评估模型的“好坏”。对于最终选定和训练好的模型,我们用“测试集”来评估模型的泛化能力。“训练集”、“测试集”和“验证集”的数据均不能有重叠,通常三个数据集的划分比列为:8:1:1。虽然在平时表述的时候,我们通常不会严格的区分“测试集”和“验证集”(一般习惯性的都用“测试集”表述),但是为了避免混淆以及确保规范,在本书中统一使用“验证集”。另外,在本小节里,所有的数据集划分,都只是划分“训练集”和“验证集”,不涉及到“测试集”。读者可以理解为我们已经有了“训练集”和“测试集”,本小节所介绍的模型评估的方法是要在“训练集”的基础上进一步划分出“训练集”和“验证集”。
接下来我们介绍几种常见的模型评估的方法:留出法、交叉验证法、留一法(交叉验证法的一个特例)以及自助法。
(1)留出法
“留出法”(hold-out)是一种较为简单的方法,它直接将数据集划分为训练集和验证集,集合和集合是互斥的,
需要注意的是,为了确保“训练集”和“验证集”中数据分布的一致性,我们需要使用“分层采样”的方式划分数据集。举个简单的例子,假设我们的数据集中有100个样本,其中有50个正例和50个负例。我们假设训练集和验证集的样本数比例为,即训练集有80个样本,验证集有20个样本。若使用“分层采样”,则训练集中应该有40个正例和40个负例,而验证集中应该有10个正例和10个负例。
由于数据的划分具有随机性,通过一次划分数据集训练后得到的模型,在“验证集”上的表现不一定能体现出模型真正的效果。因此我们一般会多次划分数据集并训练模型,并取多次实验结果的平均值作为最终模型评估的结果。
“留出法”还存在一个问题,那就是“训练集”和“验证集”的比例该如何确定。这个问题在数据样本足够多的时候可以不用考虑,但在数据样本不是特别多的时候就会造成一定困扰,一般的做法是将的数据作为“验证集”。
(2)交叉验证法
“交叉验证法”(cross validation)将数据集划分为个大小相同,但互斥的子集,即。为了确保数据分布的一致性,这里我们同样使用“分层采样”的方式划分数据集。
对于划分得到的个数据集,我们每次使用其中的一个作为“验证集”,剩下的个作为“训练集”,将得到的个结果取平均值,作为最终模型评估的结果,我们称这种方法为“k折交叉验证”。和“留出法”一样,为了排除数据集划分的影响,我们对数据集进行次划分,每次划分得到个子集,然后进行次“k折交叉验证”,并取这次“k折交叉验证”结果的平均值作为最终的结果。我们称这种方法为“次k折交叉验证”,常见的有“5次10折交叉验证”或“10次10折交叉验证”。
“交叉验证法”有一种特殊地情况,假设我们的数据集大小为,若使得的值等于,则把这种情况称为“留一法”,因为这时我们的“验证集”中只有一个样本。“留一法”的优点是不存在数据集划分所产生的影响,但是当数据集较大时,对于样本数量为的数据集,使用“留一法”需要训练个模型,这会需要很大的计算开销。
(3)自助法
“自助法”是一种基于自助采样的方法,通过采样从原始数据集中产生一个训练集。假设我们的数据集中包含有个样本,每次随机的且有放回的从数据集中挑选出一个样本添加到数据集中,重复进行次后,我们会得到一个和原始数据集大小相同的数据集。在数据集中,样本在次采样中均不被抽到的概率为: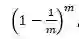
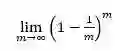
求解式1-1可以得到其值为1/e,约等于36.8%。因此,在m次采样后,数据集D中仍然有约36.8%的样本没有被抽到,我们可以用这些数据作为验证集,即: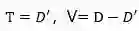
“自助法”在样本数量较少的时候比较适用,因为即使划分了验证集也并没有减少训练集的数量;此外,使用“自助法”可以从原始数据集中产生出多个互不相同的训练集,这对集成学习很有帮助。“自助法”也有缺点,因为训练集的产生是随机采样得到的,因此数据样本分布的一致性被破坏了。
下表是对几种模型评估方法的总结:
表1-1 常用的模型评估方法
评估方法 |
集合关系 |
注意事项 |
优缺点 |
留出法 (hold-out) |
要分层采样,尽可能保持数据分布的一致性;为了保证可靠性,需要重复实验后取平均值作为最终的结果。 |
训练集/测试集的划分不好控制,测试集划分的过小或者过大,都会导致测试结果的有效性得不到保证。 |
|
交叉验证法 (cross validation) |
为了排除数据划分引入的误差,通常使用“p次k折交叉验证”。 |
稳定性和保真性很大程度上取决于k的值。 |
|
留一法 (Leave-One-Out,LOO) |
交叉验证法的特例,k值取总数据集的大小。 |
不受样本划分的影响,但是当数据量较大时,计算量也较大。 |
|
自助法 (bootstrapping) |
有放回的重复采样。 |
适合在数据量较少的时候使用;有放回的采样破坏了原始数据的分布,会引入估计偏差。 |
四.模型性能度量
前面我们介绍了一些常用的模型评估的方法,有了评估的方法,我们还需要有评价的标准,才能对机器学习模型进行评估和对比。在这部分内容里我们就来了解一些用来衡量机器学习模型泛化能力的评价标准,我们称之为模型的性能度量(performance measure)。
(1)正确率(accuracy)和错误率(errorrate)
正确率与错误率是分类任务中最常用的两个评价指标,它的概念也很好理解。正确率是指分类器预测正确的数据样本数占测试集(或验证集)中样本总数的比例。相应地,错误率是指在测试集或验证集上,分类器预测错误的数据样本数占测试集(或验证集)中样本总数的比例。具体计算方式如下:
(2)查准率(precision)、查全率(recall)与F1
正确率和错误率是最为常用的性能度量指标,但在有些时候我们可能需要更细致的度量指标,举个例子,假设我们训练好了一个垃圾邮件分类的模型,这是一个简单的二分类模型,我们要用这个模型将垃圾邮件和正常邮件进行分类。模型都不会是百分之百准确的,所以这个时候就需要有一个考量。对于有些用户来说,他们希望尽可能的排除掉所有的垃圾邮件,哪怕偶尔将一些正常邮件误判为垃圾邮件。还有一些用户可能会有很多重要的邮件,所以他们希望这些重要的邮件都能正常收到,哪怕也收到少数垃圾邮件。所以,这个时候我们关心的有两点:第一点,在分类得到的“正常邮件”中有多少是真正的正常邮件;第二点,所有的正常邮件中,有多少被正确的分类了。这个时候,我们就需要有新的度量指标:查准率和查全率(也称为“召回率”)。
以二分类为例,我们把分类器的分类结果进行统计,需要统计四种数据,如下表所示:
表1-2 计算查准率和查全率时需要统计的数据
条目 |
描述 |
真正例(true positive) |
真实值(actual)= 1,预测值(predicted)= 1 |
假正例(false positive) |
真实值(actual)= 0,预测值(predicted)= 1 |
真反例(true negative) |
真实值(actual)= 0,预测值(predicted)= 0 |
假反例(false negative) |
真实值(actual)= 1,预测值(predicted)= 0 |
令TP、FP、TN和FN分别表示上述四种情况所对应的数据样本个数,根据统计的数据,我们可以做出一张表,称为“混淆矩阵(Confusion Matrix)”:
表1-3 分类结果的混淆矩阵
真实值 预测值 |
正例(positive) |
反例(negative) |
|
正例(positive) |
TP(真正例) |
FN(假反例) |
|
反例(negative) |
FP(假正例) |
TN(真反例) |
查准率(precision)与查全率(recall)的定义如下:
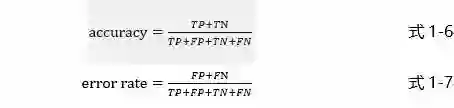
相应地,正确率(accuracy)和错误率(error rate)可以表示为:
下面我们看一个简单的例子,这是一个三分类的例子。假设我们需要实现猫、狗和兔子的分类,我们用训练好的模型对测试集(约定测试集中每个类别有1000个数据样本)进行判别。我们得到了如下表所示的混淆矩阵:
表1-4 三分类结果的混淆矩阵
真实值 预测值 |
猫 |
狗 |
兔子 |
猫 |
812 |
88 |
132 |
狗 |
60 |
908 |
70 |
兔子 |
132 |
32 |
798 |
对应上面的混淆矩阵,我们可以将其拆成三个二分类的矩阵,以猫为例:
表1-5 对于猫的二分类混淆矩阵
真实值 预测值 |
猫 |
狗、兔子 |
猫 |
TP = 812 |
FN = 88+100 |
狗、兔子 |
FN = 60+132 |
TN = (908+32)+(70+798) |
根据公式1-4与公式1-5可得:
在绝大多数情况下,查准率(precision)和查全率(recall)总是相对立的,当查准率高的时候,查全率往往会偏低,而当查全率高的时候,查准率又会偏低。例如我们前面提到的垃圾邮件过滤的例子,我们如果想要尽可能的过滤掉垃圾邮件,那就免不掉会把一些正常邮件也误判为垃圾邮件;如果我们想要尽可能的保留所有的正常邮件,那就免不了也会保留一些垃圾邮件。所以,在通常情况下,我们需要根据自己的实际需要来设定一个合适的阈值,使得查准率和查全率的平衡点能最好的满足我们的需求。
在以正确率和错误率作为模型的评价指标时,我们可以简单的通过比较两个模型的正确率来判断孰优孰劣。那在以查准率和查全率为评价指标时,我们要如何比较呢。一般常见的有两种方法,一种是做“P-R图”,另一种是计算“F1”度量值。这里本书选择介绍后者,这是一种更常用、更直接的度量方法,在阿里天池、Kaggle等比赛中,也都是使用“F1”度量作为模型的评价指标,它是查准率和查全率的一种加权平均。
度量的计算公式如下:(约定用P表示查准率(precision),R表示查全率(Recall)):
由于在不同情况下我们对查准率和查全率的侧重不同,所以我们需要有一个一般形式的度量,记为
上式中,当的值大于1时,代表模型的评价更侧重于查全率,当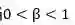
五.参考文献
[1] ATUTORIAL ON PRINCIPAL COMPONENT ANALYSIS Derivation, Discussion and SingularValue Decomposition, Jon Shlens , 2003
[2] David M. Blei, Andrew Y. Ng, and Michael I. Jordan. Latentdirichlet allocation. J. Mach. Learn. Res.,3:993–1022, March 2003.
[3] Ivan Titov and Ryan McDonald. Modelingonline reviews with multi-grain topic models. In Proceeding ofthe 17th international conference on World Wide Web, WWW ’08, pages 111–120,New York, NY, USA, 2008. ACM.
[4] Independentcomponent analysis: algorithms and applications, A Hyvärinen , E Oja, 2000 , 13 (4) :411-430
欢迎扫码关注磐创AI微信公众号