研究人员提出拓扑晶体绝缘体中的d-2维边界态

2018 年 2 月 1 日 中科院之声

近日，中国科学院物理研究所/北京凝聚态物理国家实验室（筹）理论室副研究员方辰、研究员方忠和博士研究生宋志达，提出了一种全新的旋转对称性保护的三维拓扑态。这种拓扑态因具有一维拓扑表面态而区别于已知的三维拓扑绝缘体。相关成果发表在《物理评论快报》上，并且被选为编辑推荐。

在目前已知的全部拓扑绝缘体（包括拓扑晶体绝缘体Topological crystalline insulators）中，若拓扑态本身是d维的，其对应的拓扑表面态便是d-1维的。比如，二维陈-绝缘体的表面态是一维手性（chiral）态；时间反演保护的二维拓扑绝缘体的表面态是一维螺旋（helical）态；时间反演保护的三维拓扑绝缘体的表面态是二维狄拉克点；滑移面保护的三维拓扑晶体绝缘体的表面态是二维沙漏费米子，等等。那么，是否存在一种d维拓扑绝缘体，具有d-2维的表面态呢？

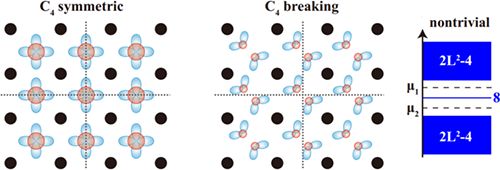
研究人员意识到，可以相当直接地在二维系统中构造零维边界态。考虑图1（左）中左侧的共价绝缘体，假设原子在黑点上，形成共价键之后，电荷中心却在花瓣处，每个花瓣上有四个电子。那么，当沿着图中虚线切开这个系统时，一个电荷中心被分成四份，每份一个电子，每个角各得一个电子。由于这个电子没有配对，因此每个角上会有一个悬挂键，这个悬挂键就是零维边界态。必须注意到，这种零维表面态只有存在四度旋转对称性时才有意义，否则，可以按图1（中）的方式把电子两两配对，使得每个角上都没有悬挂键。

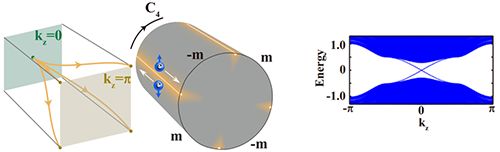
然而，这个态不是拓扑非平庸的：它依然是个原子绝缘体，只是电荷中心与原子位置不重合而已。而后，研究人员把这一思想扩展到三维。考虑一个有四度旋转对称性、时间反演对称性的三维系统，并把z方向（转轴方向）变换到动量空间。其中，k_z=0与k_z=π两个面都有时间反演对称性，而其它的k_z面则没有时间反演对称性。因此，之前对二维系统的讨论仅适用于k_z=0与k_z=π两个面。于是，人们可以构造这种态：k_z=0的二维子系统的电荷中心在原胞中心，k_z=π的二维子系统的电荷中心在原胞角上，而0<k_z<π的子系统通过一个旋转不变的过程把它俩连起来。在这样的系统中，尽管每个k_z子系统都是某种二维原子绝缘体，但由于电荷中心的流动，三维系统则是拓扑非平庸的。在图2（左）中，研究人员画出了这种电荷流。根据这种电荷流，可以推测出如图2（中）所示的一维螺旋态。为了验证这一猜想，研究人员构造紧束缚模型并进行数值验证，在图2（右）展示了在一个方形四棱柱上的一维能带结构，其中的无能隙激发即为一维螺旋态。需要注意的是，这种一维螺旋态不一定出现在棱上：通过加入一个保持四度旋转的扰动项，可以把它旋转到任何位置。因此，即便在如图2（中）所示的光滑表面上，依然有这种一维态。

研究人员将上述模型拓展到一般情形，提出了一个在三维系统中由四重旋转对称性和时间反演不变性所共同保护的Z₂型拓扑不变量。该不变量不为零时，体系属于一类新的三维拓扑晶体绝缘体，其特点就是在侧表面上有四条一维螺旋态，而不是二维边界态。为了便于在实际材料中搜索此类新型拓扑量子态，研究人员利用“对称性指标”理论找到计算拓扑不变量的简易表达式。利用一维螺旋态的无背散射的特性，用此类新材料制成的纳米线可以制成新型量子器件，用于超低能耗的信号传输。

研究工作得到了科技部重点研发项目以及国家自然科学基金委面上项目的资助。