加入极市专业CV交流群,与10000+来自腾讯,华为,百度,北大,清华,中科院 等名企名校视觉开发者互动交流!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 , 回复 加群, 立刻申请入群~
作者:akkaze-郑安坤
知乎链接:https://zhuanlan.zhihu.com/p/99193115
本文 已由作者授权转载,未经允许,不得二次转载。
图像本身可以被理解成一种二维平面上的分布。更广泛的说,就是二维多分量函数(考虑通道,通道就是分量),这些分布或者函数本身也可以被划分成不同的函数族,直观的说,前景是猫和前景是狗的图像可以被看成是两族函数,这种划分不是唯一的,是由task决定的。
cnn可以被理解为作用在其上的泛函,把 这样函数空间映射到另一族函数空间,换句话说,cnn是场到场的变换,比如高度场到温度场,一般说来,泛函是指函数(也就是场)到函数的变换,或者函数到标量或者向量的变换。
注意,本文中的函数,场,分布的意思接近,场和标量或者变量的区别在于场有自变量空间, 通常就是坐标平面。
cnn是一个泛函,从源函数空间映射到目标函数空间。 而反过来,知道了这样一个映射,也能刻画源函数空间的性质,因为一般目标函数空间都相对简单( 对于分割这种任务而言,目标函数空间就是定义在坐标平面上的多变量函数,每个坐标的值都是一个one-hot向量,向量值的变化发生在图像边缘处 )。
场到向量的变换,可以直接从场到场的变换得到,只需要在每个分量上对函数进行全平面积分即可,类似的手段也是可以的,目的是去掉自变量。 例如,在分割的基础上进行分类,只需要把global average pooling即可,它就是全平面上的积分,所以我们现在认为源函数空间和目标函数空间都是定义在一个坐标平面上的场。
我们知道一般的神经网络几乎能够拟合任意有界函数,universal approximation theorem告诉我们如果函数
的定义域和值域都是有界的,那么一定存在一个三层神经网络
,它几乎处处以指定的误差逼近
,这是普通的nn。
但是如果我们回到卷积神经网络,我们会发现我们的输入是一个有界信号(准确的说是满足一定分布的一族有界信号),输出也是一个有界信号,我们需要拟合的是函数族到函数族的一个变换,即存在有界函数
和有界函数
,其中
本身也是有界的,我们需要的是一个变换
这其实是一个泛函,也就是函数的函数,(如果我们把所有分辨率的32x32图像信号当成一族函数(另外,如果使用0延拓或者随机延拓,这个函数可以被当成定义在全空间上的函数),那么边缘提取正是一阶微分算子,它就是一个泛函,在图像中,它几乎是最重要的泛函,它的离散形式是sobel算子,它作用在图像上,得到边缘响应,这也是一族有界函数,响应经过限制后依然有界)。
在
数学上,如果一个泛函输入是有界的,输出是有界的,就说这个泛函是有界的。
另外函数族的概念需要着重说一下,举个例子,包含猫的图像和包含狗的图像其实是两个函数族,当然task不同的情况下,也可以看成是一个函数族,分类任务就是把这些
函数族映射到常函数上,或者onehot函数上(泛函可以把场变换成标量或者向量,不必定义在全空间上,但是其实如果把分类看成分割的子问题的话,这一步只差一个global average pooling,一个全空间积分)。
<img src="https://pic3.zhimg.com/v2-515bd3cb3abf79139eaad77d82f3bcda_b.jpg" data-rawwidth="430" data-rawheight="224" data-size="normal" class="origin_image zh-lightbox-thumb" width="430" data-original="https://pic3.zhimg.com/v2-515bd3cb3abf79139eaad77d82f3bcda_r.jpg"/><mpchecktext contenteditable="false" id="1582711742481_0.482749469398949"></mpchecktext><mpchecktext contenteditable="false" id="1582711742549_0.9605098370626075"></mpchecktext><mpchecktext contenteditable="false" id="1582711742656_0.5538131915111065"></mpchecktext><mpchecktext contenteditable="false" id="1582722111474_0.5516045230212165"></mpchecktext>
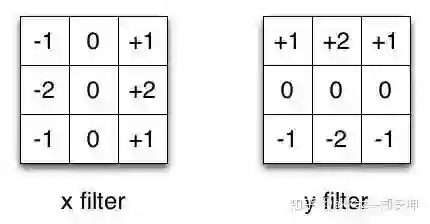
著名的sobel算子,它被用来求取图像边缘,它也是一阶微分的离散形式
<img src="https://pic3.zhimg.com/v2-20760c5ab5e2a3aded16e15d804a9952_b.jpg" data-rawwidth="547" data-rawheight="342" data-size="normal" class="origin_image zh-lightbox-thumb" width="547" data-original="https://pic3.zhimg.com/v2-20760c5ab5e2a3aded16e15d804a9952_r.jpg"/><mpchecktext contenteditable="false" id="1582711742483_0.5126221833743351"></mpchecktext><mpchecktext contenteditable="false" id="1582711742551_0.24969593058450856"></mpchecktext><mpchecktext contenteditable="false" id="1582711742658_0.08232105861834882"></mpchecktext><mpchecktext contenteditable="false" id="1582722111476_0.36712582082973033"></mpchecktext>
原图像的值域是有界的(0—255),那么sobel算子的输出也是有界的
另外传统cnn中不需要采样,这样输入和输出函数的定义域就是相同的(这也说明,对于卷积神经网络,只有卷积是必不可少的,其他的运算都可以没有),也就是说输入输出函数被定义在同一定义域上。
要拟合这样一个变换,在广义函数理论里面,最容易并且直接想到的这样一个变换,就是卷积:
它有平移不变性,这几乎是这样一种泛函所必须的性质,我们希望原函数有一个平移的同时,目标函数一定有同样的平移
原函数和卷积核变宽或者变窄的同时,像函数也会随之变宽或者变窄,在相差一个缩放因子的意义上,事实上这个变换不是尺度不变性,而是尺度等变性,但是这样一个性质也是很有用的。
同时,卷积也有结合律与交换律
前者意味着,如果多个卷积作用在函数上,其实相当于一个更大的卷积作用在函数上。
在分析里面,我们通常用
来记函数
的支撑集,这是函数取值不为0的地方,同时可以证明
,这里使用点集相加,其定义为,
,其中加法就是简单的数值加法,这意味着你总可以用多个支撑集更小的卷积核合成一个支撑集更大的卷积核。
这样一个函数并不存在,但是我们可以考虑用其他函数逼近它,比如高斯函数。
它的卷积有如下性质,
这意味着与它的导数作卷积可以很容易得到原函数的各阶导数,而导数是函数最重要的性质。
直接用一个卷积不明智,我们也不知道如何去拟合它,但是我们可以用一系列卷积去拟合泛函变换,
平移不变性依然存在,但是尺度不变性没有了,但是如果非线性函数其实是分段线性函数,例如ReLU,其实尺度不变性依然能保留下来。
原因是尺度不变多出来一个因子,这个因子被非线性作用一次之后就没有了(线性被非线性作用一次 ,就没有线性关系了),但是分段线性函数却能叠乘这个因子,如果层数固定,那么这个泛函依然具有尺度等变性。
这是单分量的形式,事实上
必定不止一个分量,正确形式应该是
,而且中间过程也不应该是单分量的,结果也不应该是单分量的,其中一个分量如下,其他类似,
每次加权都会产生新的分量,相当于卷积神经网络中间产生的新通道,中间这些分量就是中间通道,输入输出都是多通道。
对上面的公式进一步的解释如下,多分量函数就是多通道特征图,对每个分量用depwise作用之后加权相加,这样得到一个新的函数分量。
然后这样的操作重复多次,得到多个输出分量,注意,重复同样的计算过程,但是用的depwise卷积核不同。
考虑到如果从数学上去拟合,我们希望
都是在某一个函数空间里,或者说强制它们在一个函数空间里,然后研究这个空间的性质,这样一来它们就可以在这个函数空间里被基底函数展开,展开的好处是共享的卷积核变多了,
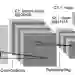
展开类似于线性加权,而这类似于可分离卷积神经网络,设计成这样是参考了论文Depthwise Convolution is All You Need for Learning Multiple Visual Domains其中加权的过程正是1x1卷积,
<img src="https://pic3.zhimg.com/v2-d7186990d31023a7cd86b3e21909b922_b.jpg" data-rawwidth="757" data-rawheight="230" data-size="normal" class="origin_image zh-lightbox-thumb" width="757" data-original="https://pic3.zhimg.com/v2-d7186990d31023a7cd86b3e21909b922_r.jpg"/><mpchecktext contenteditable="false" id="1582711742511_0.5417109456778477"></mpchecktext><mpchecktext contenteditable="false" id="1582711742579_0.0023399133100987513"></mpchecktext><mpchecktext contenteditable="false" id="1582711742686_0.010967429221768854"></mpchecktext><mpchecktext contenteditable="false" id="1582722111501_0.9090852551418562"></mpchecktext>
左边每个通道独立做卷积,右边1x1卷积相当于加权
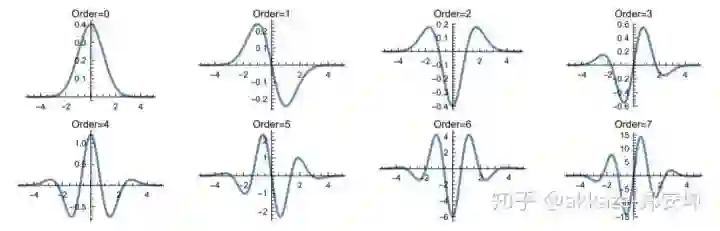
我们选择高斯函数(其实还有更多的选择,比如著名的gabor小波)及其导数作为基底函数,它们构成了高斯小波基,
事实上不同的基底函数表征了这个task,中间的函数空间(也就是各层特征图)分布也决定了这个网络的全部性质,也就是说输入函数族如何被映射到输出函数族上,对于处理不同task的cnn,比如分类猫狗的,分类鸡鸭的,哪怕结构完全相同,其中间函数分布也完全不一样,这里固定住只是为了后面的实验,证明这种结构有足够的拟合能力。
<img src="https://pic1.zhimg.com/v2-4e36db86184d45781223fc4b4d999ad0_b.jpg" data-rawwidth="1064" data-rawheight="341" data-size="normal" class="origin_image zh-lightbox-thumb" width="1064" data-original="https://pic1.zhimg.com/v2-4e36db86184d45781223fc4b4d999ad0_r.jpg"/><mpchecktext contenteditable="false" id="1582711742515_0.8997784651806321"></mpchecktext><mpchecktext contenteditable="false" id="1582711742583_0.9784424950709494"></mpchecktext><mpchecktext contenteditable="false" id="1582711742690_0.9960834616381266"></mpchecktext><mpchecktext contenteditable="false" id="1582722111505_0.5908532275349654"></mpchecktext>
高斯小波基
构造这样一个卷积神经网络,这里的卷积神经网络没有任何下采样,采用和我的另一篇文章相似的架构,并在cifar100上训练(冻结所有的depthwise,证明即使函数空间的选取不是完全正确,一个正确的加权也足以得到比较好的结构),结果如下:
<img src="https://pic3.zhimg.com/v2-0747bc0ec00102f672c516e1110a48fe_b.jpg" data-rawwidth="640" data-rawheight="480" data-size="normal" class="origin_image zh-lightbox-thumb" width="640" data-original="https://pic3.zhimg.com/v2-0747bc0ec00102f672c516e1110a48fe_r.jpg"/><mpchecktext contenteditable="false" id="1582711742518_0.47827169726526086"></mpchecktext><mpchecktext contenteditable="false" id="1582711742586_0.6756893522367471"></mpchecktext><mpchecktext contenteditable="false" id="1582711742693_0.6429240514514023"></mpchecktext><mpchecktext contenteditable="false" id="1582722111508_0.9325436638790859"></mpchecktext>
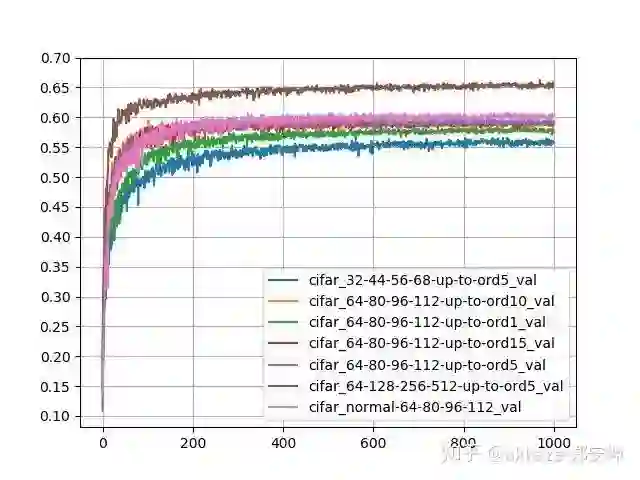
预测精度
<img src="https://pic2.zhimg.com/v2-dae31cc0e69a6a62a17a2371a0ffe82d_b.jpg" data-rawwidth="640" data-rawheight="480" data-size="normal" class="origin_image zh-lightbox-thumb" width="640" data-original="https://pic2.zhimg.com/v2-dae31cc0e69a6a62a17a2371a0ffe82d_r.jpg"/><mpchecktext contenteditable="false" id="1582711742520_0.5945252897473671"></mpchecktext><mpchecktext contenteditable="false" id="1582711742588_0.2260397649590079"></mpchecktext><mpchecktext contenteditable="false" id="1582711742695_0.6128031781995804"></mpchecktext><mpchecktext contenteditable="false" id="1582722111510_0.9216382599658891"></mpchecktext>
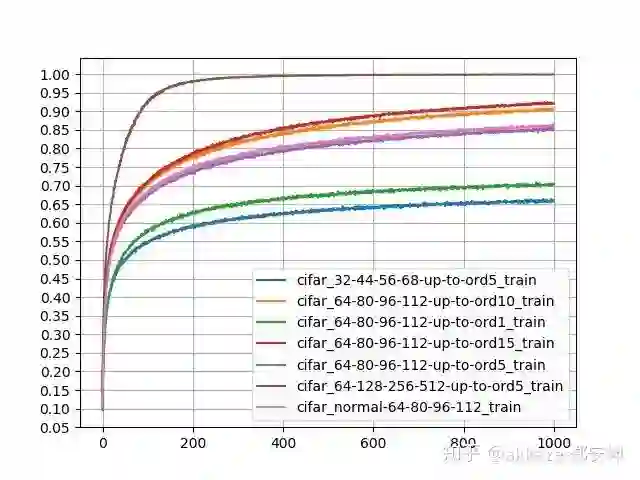
训练精度
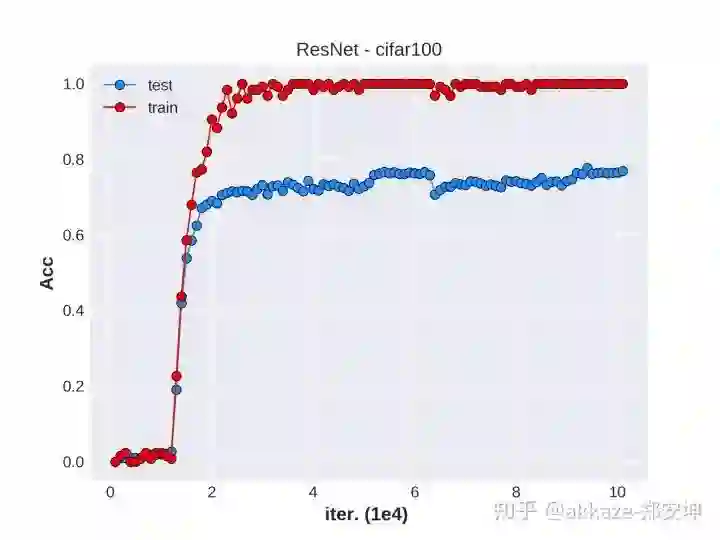
然后补上resnet在cifar100上的结果作为baseline
<img src="https://pic4.zhimg.com/v2-3ca257cc3ea7ccfad1c3407e60d801af_b.jpg" data-rawwidth="2048" data-rawheight="1536" data-size="normal" data-caption="" class="origin_image zh-lightbox-thumb" width="2048" data-original="https://pic4.zhimg.com/v2-3ca257cc3ea7ccfad1c3407e60d801af_r.jpg"/><mpchecktext contenteditable="false" id="1582711742523_0.4818412436364419"></mpchecktext><mpchecktext contenteditable="false" id="1582711742591_0.5341783839696412"></mpchecktext><mpchecktext contenteditable="false" id="1582711742698_0.6421561198719488"></mpchecktext><mpchecktext contenteditable="false" id="1582722111513_0.7389203739650516"></mpchecktext>
label里面的前四个数字表示前四层的1x1卷积的通道数,ord后面指使用到高斯导数的阶数,原函数的阶数为0,对于每个通道,使用depth-multiplier控制高斯导数的阶数,对每个通道而言,作用在其上的depwise-conv是相同的,也就是说如果有3个通道,使用到5阶高斯导数,那么每个通道的5个depwise-conv是相同的,这实际上相当于参数冗余了。最后一个normal表示用正态分布初始化(he-initialization)。
纵向比较,四个通道数相同,都是64-80-96-112的网络,使用高斯导数的阶数为1,5,10,15,发现只有ord1的预测精度偏低,但是ord5,ord10,ord15的预测精度极为相近,说明CNN可能对高阶的导数不敏感(至少在图像识别中是如此),同时,随着阶数提升,训练精度是逐个增加的,说明确实有过拟合。横向比较,都使用5阶高斯导数,但是通道数分别为32-44-56-68,60-80-96-112,64-128-256-512,发现预测精度和训练精度都是同步增加,说明通道数确实有利于组合出更多的函数出来。
最后一个正态的结果作为参考,因为有depth-multiplier的情况下,使用正态分布随机初始化,会造成实际参数更多,所以这个比较并不是特别公平,但是可以看到CNN的巨大学习能力,使用这样随机初始化依然能够有好的结果。
同
时这里的方法过于大胆,事实上对于普通的分类分割网络,浅层确实可以用一些常用函数来表示,比如gabor小波基,论文gaborconvet采用了这样的思想。同时注意到,对于深层,这里的基函数需要能反应这个分类或者分割问题的特征空间,而通过学习出来的卷积所构成的基函数,恰好反应了这一特征空间的实际分布。
对于普通的神经网络,每一层都是在变换输入分布或者中间分布,通过研究每一层的函数空间分布我们就能很好的研究这个多层卷积神经网络的性质。
如果我们把图像看成函数族,那它们也应该有它们的分布,任意图像就是定义在某一块区域,比如32x32上的下界为0,上界为255的任意连续(甚至连续这个条件都可以放宽)函数组成的函数族。大多数cnn的第一层行为都非常类似于边缘提取,而边缘图像本身就可以一系列脉冲来描述,这是cnn第一层的函数空间。对于分割,最后一层通常是一个多分量的二值函数空间,对于每个点,都对应一个onehot向量。分类问题可以看成分割之后在全空间积分,而这正是常用的global average pooling。
点击 阅读原文 ,可跳转浏览本文内所有网址链接
极市平台视觉算法季度赛,提供真实应用场景数据和免费算力,特殊时期,一起在家打比赛吧!
添加极市小助手微信
(ID : cv-mart) ,备注:
研究方向-姓名-学校/公司-城市 (如:目标检测-小极-北大-深圳),即可申请加入
目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割等极市技术交流群
,更有
每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、 干货资讯汇总、行业技术交流 ,
一起来让思想之光照的更远吧~
△长按添加极市小助手
△长按关注极市平台,获取 最新CV干货
觉得有用麻烦给个在看啦~