图，这个玩意儿竟然还可以用来排序！

会员服务 ·

图，这个玩意儿竟然还可以用来排序！

2018 年 10 月 15 日 算法与数据结构

来自：程序员私房菜（微信号：eson_15）

阅读本文大概需要6分钟

之前我写过一篇深度技术文：我敢说，这图绝对跟你想象中的不太一样！在这篇文章里我详细分析了图这种数据结构。

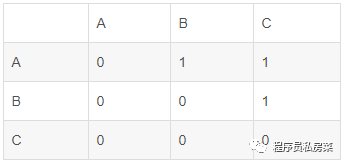
本文是基于图这种数据结构，介绍一个排序算法：拓扑排序。准确的说，应该叫“有向图的拓扑排序”。所谓的有向图，就是 A -> B，但不能 B -> A。与无向图的区别是，它的边在邻接矩阵里只有一项（这些东西，我在上面的文章中都有详细的描述）。

有向图的邻接矩阵如下：

所以针对前面讨论的无向图，邻接矩阵的上下三角是对阵的，有一半信息是冗余的。而有向图的邻接矩阵中所有行列值都包含必要的信息，它的上下三角不是对称的。所以对于有向图，增加边的方法只需要一条语句即可：

//有向图中，邻接矩阵中只有一项
public void addEdge(int start, int end) {
  adjMat[start][end] = 1;
}

如果使用链表，那么 A->B表示A在它的链表中有B，但是B的链表中不包含A，这里就不多说了，本文主要通过邻接矩阵实现。

因为图是有向的，假设A->B->C->D这种，那这就隐藏了一种顺序，即要想到D，必须先过C，必须先过B，必须先过A。它们无形中形成了一种顺序，这种顺序在实际中还是用的挺广泛的，比如，要做web开发，必须先学java基础等等，这些都遵循一个顺序，所以拓扑排序的思想也是这样，利用有向图特定的顺序进行排序。但是拓扑排序的结果不是唯一的，比如A->B的同时，C->B，也就是说A和C都能到B，所以用算法生成一个拓扑排序时，使用的方法和代码的细节决定了会产生那种拓扑排序。

拓扑排序的思想虽然不寻常，但是却很简单，有两个必要的步骤：

1.找到一个没有后继的顶点；
2.从图中删除这个顶点，在列表中插入顶点的标记。

然后重复1和2，直到所有顶点都从图中删除，这时候列表显示的顶点顺序就是拓扑排序的结果了。但是文末需要考了一种特殊的有向图：那就是环。即A->B->C->D->A。这种必然会导致找不着“没有后继的节点”，这样便无法使用拓扑排序了。

下面我们来分析一下拓扑排序的代码：

public void poto() {
  int orig_nVerts = nVerts; //记录有多少个顶点
  while(nVerts > 0) {
    //返回没有后继顶点的顶点
    int currentVertex = noSuccessors(); //如果不存在这样的顶点，返回-1
    if(currentVertex == -1) {
      System.out.println("ERROR: Graph has cycles!");
      return;
    }
    
    //sortedArray中存储排过序的顶点（从尾开始存）
    sortedArray[nVerts-1] = vertexArray[currentVertex].label;
    deleteVertex(currentVertex);//删除该顶点，便于下一次循环，寻找下一个没有后继顶点的顶点
  }
  System.out.println("Topologically sorted order:");
  for(int i = 0; i < orig_nVerts; i++) {
    System.out.print(sortedArray[i]);
  }
  System.out.println("");
}

主要的工作在while循环中进行，这个循环直到顶点数为0才退出：

1.调用 noSuccessors() 找到任意一个没有后继的顶点；
2.如果找到一个这样的顶点，把顶点放到 sortedArray 数组中，并且从图中删除这个顶点；
3.如果不存在这样的顶点，则图必然存在环。

最后 sortedArray 数组中存储的就是排过序的顶点了。下面我们分析下 noSuccessor() 方法和 deleteVertes() 方法：

//return vertex with no successors
private int noSuccessors() {
  boolean isEdge;
  for(int row = 0; row < nVerts; row++) {
    isEdge = false;
    for(int col = 0; col < nVerts; col++) {
      if(adjMat[row][col] > 0) { //只要adjMat数组中存储了1，表示row->col
        isEdge = true;
        break;
      }
    }
    if(!isEdge) {//只要有边，返回最后一个顶点
      return row;
    }
  }
  return -1;
}
 
private void deleteVertex(int delVertex) {
  if(delVertex != nVerts -1) {
    for(int i = delVertex; i < nVerts-1; i++) { //delete from vertexArray
      vertexArray[i] = vertexArray[i+1];
    }
    //删除adjMat中相应的边
    for(int row = delVertex; row < nVerts-1; row++) {//delete row from adjMat
      moveRowUp(row, nVerts);
    }
    
    for(int col = delVertex; col < nVerts-1; col++) {//delete column from adjMat
      moveColLeft(col, nVerts-1);
    }
  }
  nVerts--;
}

从上面代码可以看出，删除一个顶点很简单，从 vertexArray 中删除，后面的顶点向前移动填补空位。同样的，顶点的行列从邻接矩阵中删除，下面的行和右面的列移动来填补空位。删除 adjMat 数组中的边比较简单，下面看看 moveRowUp 和 moveColLeft 的方法：

private void moveRowUp(int row, int length) {
  for(int col = 0; col < length; col++) {
    adjMat[row][col] = adjMat[row+1][col];
  }
}
 
private void moveColLeft(int col, int length) {
  for(int row = 0; row < length; row++) {
    adjMat[row][col] = adjMat[row][col+1];
  }
}

这样便介绍完了拓扑排序的所有过程了。

完整代码：

package graph;
/**
 * 有向图的拓扑排序：
 * 拓扑排序是可以用图模拟的另一种操作，它可以用于表示一种情况，即某些项目或事件必须按特定的顺序排列或发生。
 * 有向图和无向图的区别是：有向图的边在邻接矩阵中只有一项。
 * 拓扑排序算法的思想虽然不寻常但是很简单，有两个步骤是必须的：
 * 1. 找到一个没有后继的顶点
 * 2. 从图中删除这个顶点，在列表的前面插入顶点的标记
 * 重复这两个步骤，直到所有顶点都从图中删除，这时，列表显示的顶点顺序就是拓扑排序的结果。
 * 删除顶点似乎是一个极端的步骤，但是它是算法的核心，如果第一个顶点不处理，算法就不能计算出要处理的第二个顶点。
 * 如果需要，可以再其他地方存储图的数据(顶点列表或者邻接矩阵)，然后在排序完成后恢复它们。
 * @author eson_15
 * @date 2016-4-20 12:16:11
 * 
 */
public class TopoSorted {
    private final int MAX_VERTS = 20;
    private Vertex vertexArray[]; //存储顶点的数组
    private int adjMat[][]; //存储是否有边界的矩阵数组, 0表示没有边界，1表示有边界
    private int nVerts; //顶点个数
    private char sortedArray[]; //存储排过序的数据的数组

    public TopoSorted() {
        vertexArray = new Vertex[MAX_VERTS];
        adjMat = new int[MAX_VERTS][MAX_VERTS];
        nVerts = 0;
        for(int i = 0; i < MAX_VERTS; i++) {
            for(int j = 0; j < MAX_VERTS; j++) {
                adjMat[i][j] = 0;
            }
        }
        sortedArray = new char[MAX_VERTS];
    }

    public void addVertex(char lab) {
        vertexArray[nVerts++] = new Vertex(lab);
    }

    //有向图中，邻接矩阵中只有一项
    public void addEdge(int start, int end) {
        adjMat[start][end] = 1;
    }

    public void displayVertex(int v) {
        System.out.print(vertexArray[v].label);
    }

    /*
     * 拓扑排序
     */
    public void poto() {
        int orig_nVerts = nVerts; //remember how many verts
        while(nVerts > 0) {
            //get a vertex with no successors or -1
            int currentVertex = noSuccessors();
            if(currentVertex == -1) {
                System.out.println("ERROR: Graph has cycles!");
                return;
            }

            //insert vertex label in sortedArray (start at end)
            sortedArray[nVerts-1] = vertexArray[currentVertex].label;
            deleteVertex(currentVertex);
        }
        System.out.println("Topologically sorted order:");
        for(int i = 0; i < orig_nVerts; i++) {
            System.out.print(sortedArray[i]);
        }
        System.out.println("");
    }

    //return vertex with no successors
    private int noSuccessors() {
        boolean isEdge;
        for(int row = 0; row < nVerts; row++) {
            isEdge = false;
            for(int col = 0; col < nVerts; col++) {
                if(adjMat[row][col] > 0) {
                    isEdge = true;
                    break;
                }
            }
            if(!isEdge) {
                return row;
            }
        }
        return -1;
    }

    private void deleteVertex(int delVertex) {
        if(delVertex != nVerts -1) {
            for(int i = delVertex; i < nVerts-1; i++) { //delete from vertexArray
                vertexArray[i] = vertexArray[i+1];
            }

            for(int row = delVertex; row < nVerts-1; row++) {//delete row from adjMat
                moveRowUp(row, nVerts);
            }

            for(int col = delVertex; col < nVerts-1; col++) {//delete column from adjMat
                moveColLeft(col, nVerts-1);
            }
        }
        nVerts--;
    }

    private void moveRowUp(int row, int length) {
        for(int col = 0; col < length; col++) {
            adjMat[row][col] = adjMat[row+1][col];
        }
    }

    private void moveColLeft(int col, int length) {
        for(int row = 0; row < length; row++) {
            adjMat[row][col] = adjMat[row][col+1];
        }
    }
}